
What is Hyperbola?
Imagine you have a ball in your hand. You throw the ball in the air. The moment you throw the ball in the air, it will reach a certain height and once it lost all its potential energy, it will reach the ground because of the gravitational force. If somehow, the path is visible, you will see that the ball followed the arc path. If there is a mirror in the sky (the maximum point where the ball reached), you would see the reflection of that arc which we will call hyperbola.
Definition
A hyperbola looks like a bow. It is a curve that doesn't have a specific limit. Let's focus on one side of the curve. If you focus on the right side curve, the left side curve is just a reflection of that curve with a constant distance (denoted by A and A'). If we choose any point between PF, the distance of that point from P will always be smaller than the distance of the point from PF', but, at a constant difference. In simple words, the distance of PF will always be less than the distance of PF' by some constant.


Where,
PF is the distance from P to F on the right side vertex,
PF' is the distance from P to F' on the left side vertex,
|| is the absolute value function(since distance can't be a negative value).
In this case, the constant is 2a since the distance of the vertex from the origin is "a", therefore, 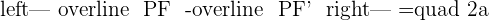 . Each bow is known as branch and F as well as F' are known as focus.
. Each bow is known as branch and F as well as F' are known as focus.
Elements of the Hyperbola
Foci
The foci are the fixed points of the hyperbola. They are denoted by F and F' in the above graph. To find the foci of the hyperbola, we use the Pythagorean theorem. The Pythagorean theorem says that the square of "c" will be equal to the sum of the square of "a" as well as square of "b".
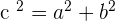
The coordinate of focus is written as 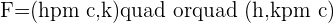 . If the transverse axis is x-axis then the focus coordinate will be
. If the transverse axis is x-axis then the focus coordinate will be 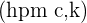 and if the transverse axis is y-axis then the coordinates of focus will be
and if the transverse axis is y-axis then the coordinates of focus will be 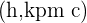 . If we talk about the origin then you will consider h and k equal to zero.
. If we talk about the origin then you will consider h and k equal to zero.
Transverse Axis or real axis
The transverse axis is the line segment between the foci. In simple words, the transverse axis is the axis that passes through both foci. One of the most frequent questions that many students ask is how to find the transverse axis? The answer is in the equation. You need to look at the equation carefully. If you notice, the hyperbola equation contains one term negative and another term positive.
If the positive sign is on the "x term" then it means the transverse axis is the abscissa. However, if the positive sign is on the "y term" that means the transverse axis is the ordinate. For example, the equation of the hyperbola is  , the transverse axis is the ordinate because the the first term (
, the transverse axis is the ordinate because the the first term (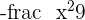 ) is negative. Another example, the equation of the hyperbola is
) is negative. Another example, the equation of the hyperbola is  , this time, the transverse axis is x-axis because the second term (
, this time, the transverse axis is x-axis because the second term (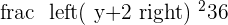 ) has a negative sign.
) has a negative sign.
Find various Maths tutor on Superprof.
Conjugate Axis or imaginary axis
The conjugate axis is the perpendicular bisector of the line segment (transverse axis). The axis perpendicular to the transverse axis is called the conjugate axis. You can also call it an imaginary axis. For instance, in the above graph, the y-axis the conjugate axis and the x-axis is the transverse axis.
Center
If you notice, hyperbola has 2 lines of symmetry. It means that if you fold the graph either in the x-axis direction or the y-axis direction, it will overlap. After folding, you will see 2 lines. The point at which both (the vertical line of symmetry and horizontal line of symmetry) intersect is known as the point of the center of the hyperbola. In conclusion, the center is the point of intersection of the axes and is the center of symmetry of the hyperbola.
Vertices
The points A and A' are the points of intersection of the hyperbola with the transverse axis. If the vertex of the parabola is opening up, we will call it the highest point on the parabola, however, if the vertex of the parabola is opening down, we will call it the lowest point on the parabola. Do note that hyperbola is made of 2 parabolas so don't get confused by the word parabola. In short, the vertices of the hyperbola is the vertex of each branch of the hyperbola.
Focal Radii
The focal radii are the line segments that join a point on the hyperbola with the foci: PF and PF'. In simple words, it is the distance from a specific point (in this case, it is P) to the foci (F & F').
Focal Length
The focal length is the line segment 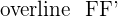 , which has a length of 2c.
, which has a length of 2c.
Semi-Major Axis
The semi-major axis is the line segment that runs from the center to a vertex of the hyperbola. Its length is a.
Semi-Minor Axis
The semi-minor axis is a line segment that is perpendicular to the semi-major axis. Its length is b.
Axes of Symmetry
The axes of symmetry are the lines that coincide with the transversal and conjugate axis. If you look carefully, the branches of hyperbola are symmetric. There are 2 axes of symmetry, the horizontal axis is called the horizontal line of symmetry and the verticle axis is called the verticle line of symmetry. The point where both axes strike each other is known as the center of the hyperbola.
Asymptotes
In the above graph, can you see a liner line between the braches of the hyperbola? They are called Asymptotes. The point at which both lines intersect is called the center of the hyperbola. Asymptotes are the lines that are very near to the branches of hyperbola but they never cross it. If the 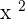 term is positive, then the equation of asymptotes will be:
term is positive, then the equation of asymptotes will be:
In case, if the 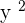 term is positive then you need to replace
term is positive then you need to replace  with
with 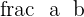 .
.
The Relationship between the Semiaxes:











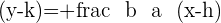




It is clear and understandable .
thankyouuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
This is very nice but please show how to find the 4p