Chapters
It is a plane curve that surrounds two focal points in such a way that for every point on the curve, the aggregate of the two distances to the focal point is the same. In other words, we can say that the ellipse is the locus of points on the plane whose sum of distances to two fixed points, foci, are always constant. You have seen the circle in which all points are at the fixed distance from the center. An ellipse seems like a squished circle.
You might have seen a conic section. It is a plane curve that traces the cone intersection with a plane, as shown in the figure below.
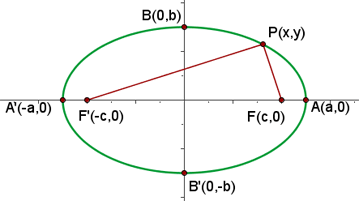

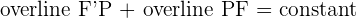

Elements of the Ellipse
Foci
The foci also known as the focus point are the fixed points of the ellipse which are present on the major axis. In figure 1.1, they are denoted by F and F'.
Major Axis
The longest diameter of an ellipse is known as the major axis. It extends from one side of the ellipse and passes through the center to the other side. It is the diameter of the wider region of the ellipse. In other words, the major axis coincides with the major diameter and passes through the center point and both foci. In figure 1.1, the major axis of the ellipse is the line segment 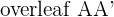 , which has a length of 2a.
, which has a length of 2a.
We have already discussed that the total distance from F' to P to F remains the same. This distance is equal to the length of the major axis.
Minor Axis
It is the shortest diameter of the ellipse and extends from one side to the other by passing through the center. It is the diameter of the narrowest region of the ellipse. We can also say that the minor axis is the perpendicular bisector (a line that divides another line into two parts) of the major axis. In figure 1.1, the minor axis of the ellipse is the line segment 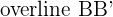 , which has a length of 2b.
, which has a length of 2b.
Focal Length
In figure 1.1, the focal length of the ellipse is the line segment 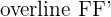 , which has a length of 2c.
, which has a length of 2c.
Center
The center of the ellipse is the point of intersection of the axes. It is the center of symmetry of the ellipse.
Vertices
The vertices of the ellipse are the points of intersection of the ellipse with the axes. They are denoted by A, A', B, and B'.
Focal Radii
The line segments that join a point on the ellipse with both foci are refereed to as the focal radii of the ellipse. They are denoted by PF and PF'.
Semi-Major Axis
Half of the major axis is known as the semi-major axis. The semi-major axis is the line segment that runs from the center of the ellipse, through a focus, and to a vertex of the ellipse. Its length is a.
Semi-Minor Axis
Half of the minor axis is referred to as the semi-minor axis. The semi-minor axis is the line segment, perpendicular to the semi-major axis, that runs from the center of the ellipse to a vertex. Its length is b.
If a = b, an ellipse is more accurately defined as a circle.
Relationship between the Semiaxes


Area of the Ellipse
The formula for finding the area of the ellipse is given below:
Area of the ellipse = 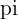 . a . b
. a . b
Here, a = length of the semi-major axis
b = length of the semi-minor axis.
Eccentricity of the Ellipse
We know that an ellipse is characterized by its squished circle or oval shape. It means that it is not perfectly round like a circle. An ellipse eccentricity measures how imperfectly round or squished an ellipse is. The eccentricity of an ellipse is given by the following equation:

The value of e is always less than 1. The reason is attributed to the fact that the foci are nearer to the center as compared to the vertices. In other words, we can say that the value is less than 1 because of 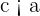 . When we have a smaller number in the numerator as compared to the denominator, we always get a value less than 1.
. When we have a smaller number in the numerator as compared to the denominator, we always get a value less than 1.
As the foci of an ellipse are moved towards the center, the shape of the ellipse becomes closer to that of the circle. If the foci of the ellipse are at the center, i.e. c = 0, then the value of eccentricity will become 0. This shows that the ellipse has taken the shape of the circle. It means that a real ellipse will always have a value of e greater than 0. Hence, we can say that  .
.
When we label any object as an ellipse, we mean to say that the shape of the object is far from being a circle.
Equation of an Ellipse
Just like the equation of the circle, an ellipse has its own equation. The equation of an ellipse in standard form having a center (0,0) and major axis parallel to the y -axis is given below:
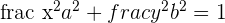
Here:
- The value of a is greater than b, i.e. a>b
- The major axis's length is equal to 2a
- The minor axis's length is equal to 2b
- The coordinates of the co-vertices are equal to

- The foci coordinates are
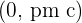 , where
, where 
Examples
Now, that you know the formula for the area of the ellipse and general equation of the ellipse, let us proceed to solve some of the examples in which we will employ both the formula and equation to find the unknown terms algebraically.
Example 1
What is the area of the ellipse having an equation  .
.
Solution
We are given the equation of the ellipse of the following form:

It shows that the value of 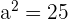 , and the value of
, and the value of 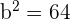 . Hence, a = 5 and b = 8.
. Hence, a = 5 and b = 8.
Now, we will put these values of a and b into the formula for finding the area of the ellipse.
Area of the ellipse = 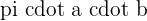
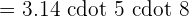
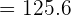
Example 2
What is the area of the ellipse having an equation 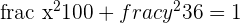 .
.
Solution
We are given the equation of the ellipse of the following form:
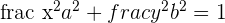
It shows that the value of 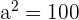 , and the value of
, and the value of 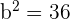 . Hence, a = 10 and b = 6.
. Hence, a = 10 and b = 6.
Now, we will put these values of a and b into the formula for finding the area of the ellipse.
Area of the ellipse = 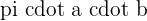
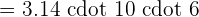
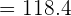
Example 3
The area of the ellipse 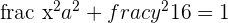 is
is  . What is the value of a?
. What is the value of a?
Solution
We know that the area of ellipse is equal to  . In the equation,
. In the equation, 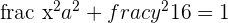 , the value of
, the value of  , hence the value of b = 4.
, hence the value of b = 4.
Area of the ellipse = 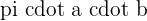
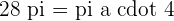
Dividing  with
with  will yield the value of a.
will yield the value of a.

Hence, the value of a is equal to 7.













It is clear and understandable .
thankyouuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
This is very nice but please show how to find the 4p