Chapters
What is a Circle?
The circle is one of the most common shapes in the world of geometry but have you ever thought what is a circle? A circle is defined as a set of points whose distances from a specific point are equal to each other. That specific point is known as the center of a circle and the distances are called the radius. This means that if we took any point of a circle and compare the distance with other point's distance, they will be equal. If this condition is void then we won't call it a circle. In other books, you might find this definition written in a different way but the meaning is the same. The other definition of a circle is the locus of points on the plane that are equidistant from a fixed point called the center. Circles have a specific equation, below is the graph of a circle:
The point C is the center of the circle and P is just a random point on the circumference. The distance from C to P is called the radius. You can take any other point beside P on the circle and you will find that the distance from the center is equal. To calculate the radius on the above graph, you need to use the distance formula.
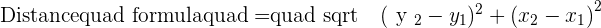
Where,
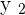and 
are the values on the ordinate,
and 
and are the values on the abscissa.
Through distance formula, you can find the value of radius. Since we are talking about circles, we will insert the above graph's data in this formula.
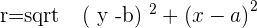
Since we are finding radius that is why we equated the right-hand side expression to the radius (which is denoted by "r"). We plugged the values of abscissa and ordinate in the equation. Now taking square on both sides to eliminate the root, it will now look like:
The above equation is the standard equation of a circle. This means that every circle's equation will be generated by the above formula.
How To Draw a Circle on a Graph Using Standard Equation
Drawing a graph of a circle is easy. You need to understand the equation properly in order to draw a perfect circle.
Let's create a circle equation which is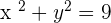 
. The next step is to compare it to a standard equation (which is ). After comparing it to the standard equation, you will notice that values of a and b are zero. Remember, the values of a and b determine the center of the circle. In short, the center of the circle is 
.
In the above equation, the center of the circle is 
because the value of a and b are zero. This means that the center lies on the origin of the graph. Place a dot on the center of the graph so that it reminds you that it is the center of the circle.
The next step is to find the radius. Again compare it with the standard equation and you will find that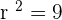 
. After simplifying it, you will find that the value of radius is 3. From the center of the circle, you need to go 3 to the right as well as 3 to the left on the abscissa. Same goes for the ordinate, 3 to the top and 3 to the bottom. Mark all these points.
Last but not least, join all the points. A geometric compass will help you to make a perfect circle. Your circle will look like this after joining all the points.
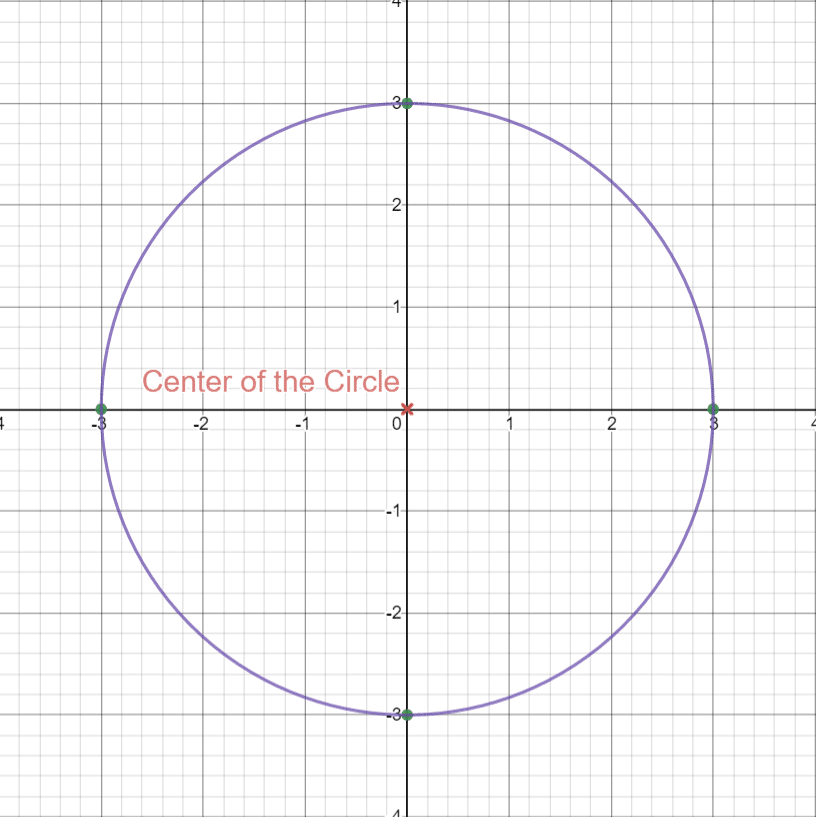
Q. Draw a circle of the following equation:
Note: The method will be same, however, the centers of the circle will be different (in the above questions). The radius will be marked according to the center of the circle.
Solution of part 1:
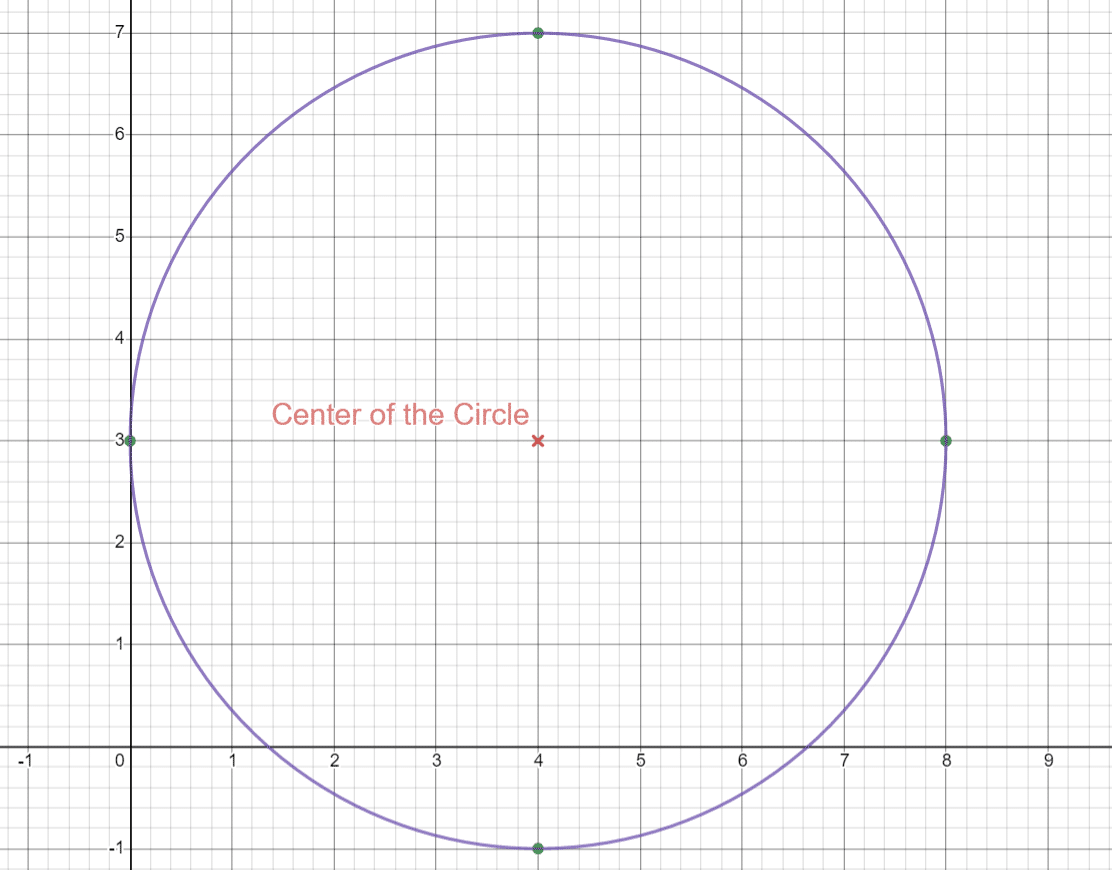
Solution of part 2:
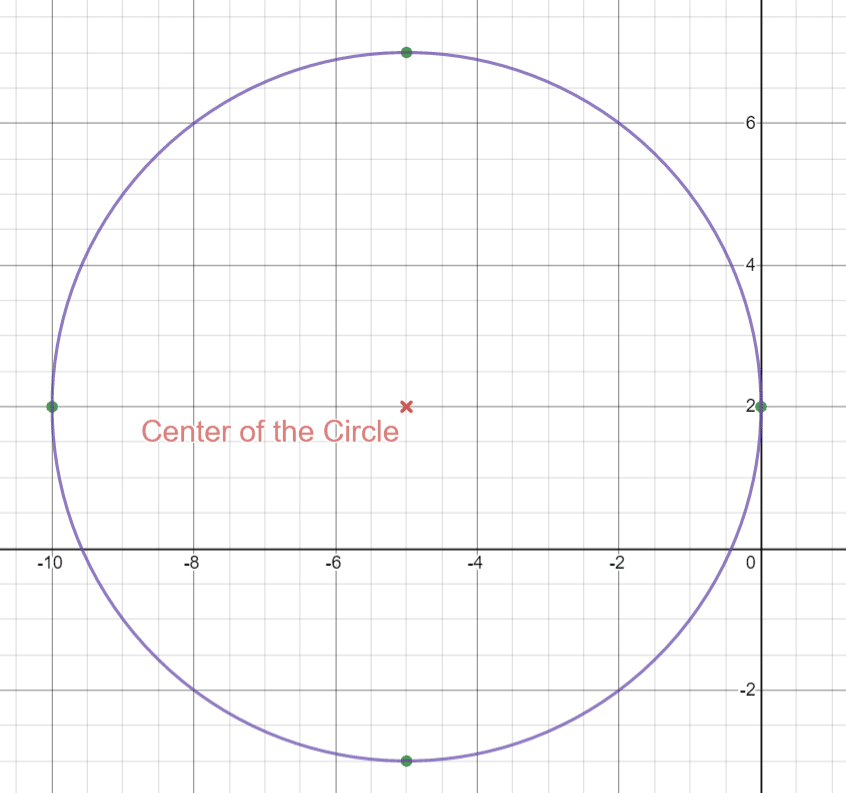
Solution of part 3:
Check out affordable Maths tuition on Superprof.
Developing the General Equation of a Circle
In order to develop the general equation of a circle, we will use the standard equation which is . If we simplify the equation, it will look like this:
Rearranging the variables:
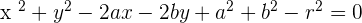
Assuming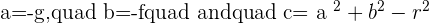 
, now the equation will be:
where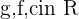 
, represents a circle, if
Let's insert all the above assumptions in the general equation.
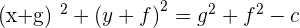
The above equation is also a modified form of the standard equation where (-g,-f) is the center of the circle and the radius is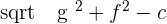 
.
Conditions For Using The Standard Equation
In order to use the standard equation, there are some conditions. If these conditions don't fulfil then you can't use the standard equation. Below are are the conditions for using the standard equation of the circle:
1. The coefficients of x² and y² should be 1. If they both have the same coefficient that does not equal 1, all terms of the equation can be divided by the value of the coefficient.
2. There is no term in xy.
3. . In some extreme cases, you might even see 
.
A Circle with the Origin as its Center
If the center of the circle lies on the origin of the graph, the equation will be reduced to:
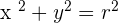
Examples
Q. Determine the equation of the circle with its center at point (3, 4) and a radius of 2.
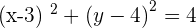
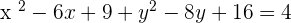
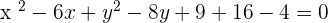
Q. Given the equation of the circle 
, find the center and its radius.
Center of circle=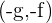 
The general equation of circle=
The general equation of this circle=
Compairing both equation and finding the center of circle and hence the center of circle is: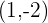 
The formula to find r is=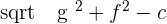
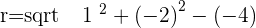
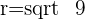
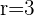
Q.Find the equation of the circle that passes through the points A = (2, 0), B = (2, 3), C = (1, 3).
Substituting values of x and y in the equation for the coordinates of the points.
Substituting values of A(2,0):
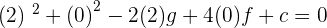
Substituting values of B(2,3):
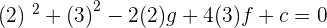
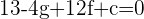
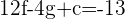
Substituting values of C(1,3):
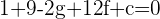
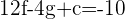
Since we have 3 different equations, after solving the above equations, we will get values of f, g and c. Place those values and the final answer will be:
Did you like this article? Rate it!
Loading...
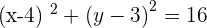
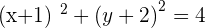
It is clear and understandable .
thankyouuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
This is very nice but please show how to find the 4p