Resuelve los siguientes problemas
1Calcular el homotético del siguiente triángulo de centro el origen y razón  , cuyos vértices son
, cuyos vértices son 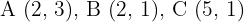 .
.
 ,
, 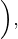
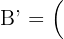 ,
, 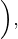
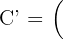 ,
, 
Como la razón de homotecia vale  , basta multiplicar en cada vértice sus coordenadas por
, basta multiplicar en cada vértice sus coordenadas por  .
.
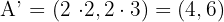 .
.
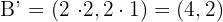 .
.
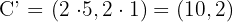 .
.

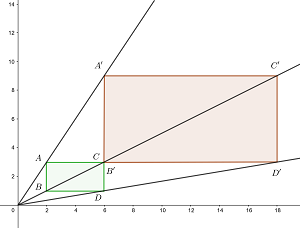
2Para el rectángulo con vértices 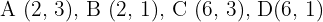 encuentre el homotético de centro el origen y razón
encuentre el homotético de centro el origen y razón  .
.
 ,
, 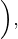
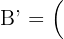 ,
, 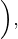
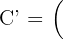 ,
, 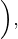
 ,
, 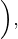
Como la razón de homotecia vale  , basta multiplicar en cada vértice sus coordenadas por
, basta multiplicar en cada vértice sus coordenadas por  .
.
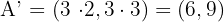 .
.
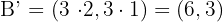 .
.
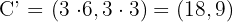 .
.
 .
.
3Para la estrella con vértices 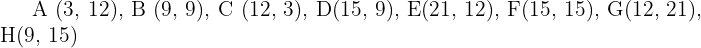 encuentre el área del homotético de centro el origen y razón
encuentre el área del homotético de centro el origen y razón  .
.
 ,
, 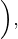
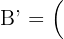 ,
, 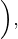
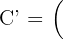 ,
, 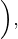
 ,
, 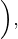
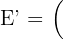 ,
, 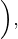
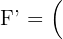 ,
, 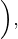
 ,
, 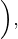
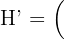 ,
, 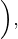
Como la razón de homotecia vale  , basta multiplicar en cada vértice sus coordenadas por
, basta multiplicar en cada vértice sus coordenadas por 
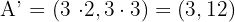 .
.
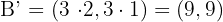 .
.
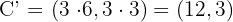 .
.
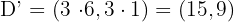 .
.
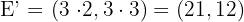 .
.
 .
.
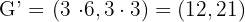 .
.
 .
.
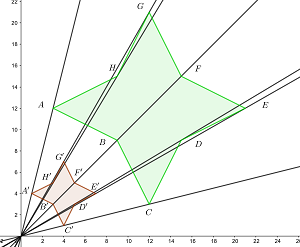
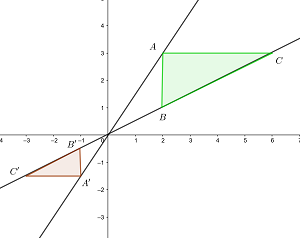
4Para el triángulo con vértices 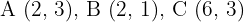 encuentre el perímetro del homotético de centro el origen y razón
encuentre el perímetro del homotético de centro el origen y razón  .
.

Como la razón de homotecia vale  , basta multiplicar en cada vértice sus coordenadas por
, basta multiplicar en cada vértice sus coordenadas por  .
.
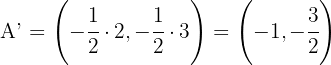 .
.
 .
.
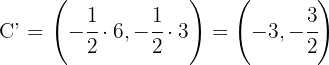 .
.
Calculamos los lados del triángulo homotético
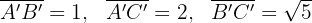 .
.
El perímetro es
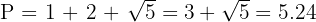 .
.
Observe que el perímetro del homotético es igual al perímetro de la figura original multiplicado por el valor absoluto de la razón dada
 .
.
5El perímetro de un polígono es de 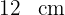 . Encuentre el perímetro
. Encuentre el perímetro  del homotético de centro
del homotético de centro  y razón
y razón  .
.


Como el perímetro del homotético es igual al perímetro de la figura original multiplicado por el valor absoluto de la razón dada
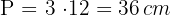 .
.
6Para el trapecio con vértices 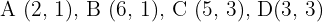 encuentre el área del homotético de centro el origen y razón
encuentre el área del homotético de centro el origen y razón  .
.
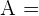
El área del homotético es igual al área de la figura original multiplicado por el cuadrado de la razón dada. El área del trapecio original es
 .
.
El área del homotético es
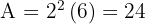 .
.

7Para la estrella con vértices 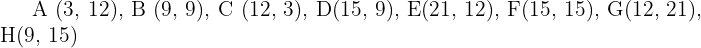 encuentre el área del homotético de centro el origen y razón
encuentre el área del homotético de centro el origen y razón  .
.
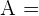
El área del homotético es igual al área de la figura original multiplicado por el cuadrado de la razón dada. El área de la estrella original está formada por un cuadrado de lado  y cuatro triángulos isósceles en con base en cada uno de los lados del cuadrado y altura
y cuatro triángulos isósceles en con base en cada uno de los lados del cuadrado y altura 
 .
.
El área del homotético es
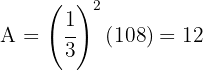 .
.

8Para el cuadrado con vértices 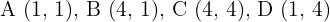 tiene por homotético al cuadrado con vértices
tiene por homotético al cuadrado con vértices 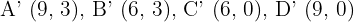 . Encuentre la razón y el centro de homotecia.
. Encuentre la razón y el centro de homotecia.
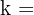 ,
,
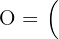 ,
, 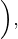
Como las figuras son homotéticas la razón del perímetro del homotético y el perímetro de la figura original es igual, en valor absoluto, a la razón de homotecia
El perímetro del cuadrado con vértices 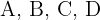 es
es  .
.
El perímetro del cuadrado con vértices 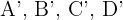 es
es  .
.
Luego la razón de homotecia (en valor absoluto) es  .
.
Para determinar el signo de la razón de homotecia tomamos dos lados paralelos entre ambas figuras y si se preserva la orientación el signo es positivo, de lo contrario el signo es negativo. Los vectores con extremos  y
y 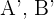 satisfacen
satisfacen
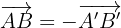
Así 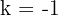 .
.
El centro de homotecia coincide con el punto medio de los vértices y sus imágenes. Para  y
y  se tiene
se tiene
 .
.
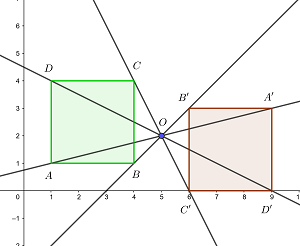
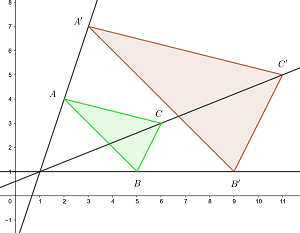
9Para el triángulo con vértices 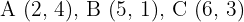 tiene por homotético al triángulo con vértices
tiene por homotético al triángulo con vértices 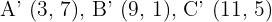 . Encuentre la razón y el centro de homotecia.
. Encuentre la razón y el centro de homotecia.
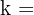 ,
,
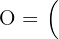 ,
, 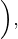
Como las figuras son homotéticas la razón de los lados paralelos es igual, en valor absoluto, a la razón de homotecia
El lado  es
es 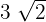 .
.
El lado  es
es 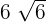 .
.
Luego la razón de homotecia (en valor absoluto) es
 .
.
Para determinar el signo de la razón de homotecia tomamos dos lados paralelos entre ambas figuras y si se preserva la orientación el signo es positivo, de lo contrario el signo es negativo. Los vectores con extremos  y
y 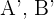 satisfacen
satisfacen

Así 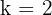 .
.
El centro de homotecia junto con  son los extremos del segmento cuyo punto medio es
son los extremos del segmento cuyo punto medio es  , luego
, luego
 .
.
10Dada la circunferencia de centro  y radio
y radio 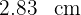 , calcular su homotética sabiendo que el centro de homotecia es el origen y la razón
, calcular su homotética sabiendo que el centro de homotecia es el origen y la razón  .
.
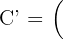 ,
, 
Si dos circunferencias son concéntricas, ¿su centro de homotecia es el mismo?
¿Y si son exteriores?
La razón es  , por tanto basta multiplicar por
, por tanto basta multiplicar por  las coordenadas del centro de la circunferencia para obterner las coordenadas de la circunferencia homotética. El radio de la nueva circunferencia no varía, es decir, mide
las coordenadas del centro de la circunferencia para obterner las coordenadas de la circunferencia homotética. El radio de la nueva circunferencia no varía, es decir, mide 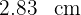 . Obsérvese que un punto arbitrario
. Obsérvese que un punto arbitrario  de la circunferencia se transforma en su opuesto
de la circunferencia se transforma en su opuesto 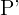 como se ve en la figura.
como se ve en la figura.
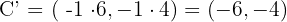

Cuando las circunferencias son concéntricas su centro de homotecia sí es el mismo, mientras que cuando son exteriores no es el mismo, el centro de homotecia es el punto donde se cortan las tangentes exteriores.
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Sean u = 2i − 3j y v = −4i + 6j. Encuentre: 4v − 6u , con su bosquejo
Al trasladar el punto A(2,4) dado el vector B(2-2) se obtiene?
Hola, de la matriz que calcularon la determinante no es =0.
Podrías señalar el ejercicio para rectificar por favor.
Calcular x²+1
Cómo resolver los ejercicios si están en kilómetros por ejemplo:
A= 300km b=4,000km C= 5,000km
Osea cuando sustituimos tenemos que poner √(X1,X2)² + (Y1,X2)²
O (X2,X1)² +(Y2,Y1)²
¿Cual de las dos?
Depende de que quieras obtener y que significa la expresión (X1,X2), la expresión √(X1,X2)² + (Y1,X2)² esta mal escrita si quieres encontrar una distancia.
24 4 70 NE
Vectores modelo