Resuelve los siguientes problemas:
1Calcular los simétricos de los puntos 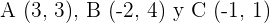 respecto del origen.
respecto del origen.
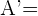 ,
, 
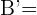 ,
, 
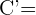 ,
, 
Calcular los simétricos de los puntos  ,
,  y
y 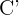 respecto del punto
respecto del punto 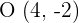 .
.
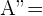 ,
, 
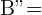 ,
, 
 ,
, 
Cuando nos indican que debemos hallar los puntos simétricos esto significa que debemos hallar los puntos simétricos respecto al origen. Es decir, multiplicamos cada uno de los puntos por  . Por lo tanto los punto simétricos serán,
. Por lo tanto los punto simétricos serán,

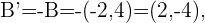
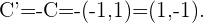
La siguiente figura nos da una descripción graficas de estos puntos.

Para el segundo caso, tenemos que hallar los punto simétricos de  ,
,  y
y 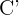 con respecto a
con respecto a 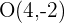 . Para esto debemos trazar un plano sobre el punto
. Para esto debemos trazar un plano sobre el punto  y hallar la simetría en este plano. Con esta idea en mente tenemos que nuestros puntos simétricos estan dados por
y hallar la simetría en este plano. Con esta idea en mente tenemos que nuestros puntos simétricos estan dados por
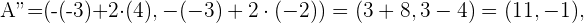
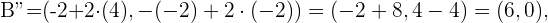
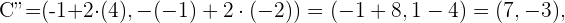
La siguiente figura nos da una descripción graficas de estos puntos.
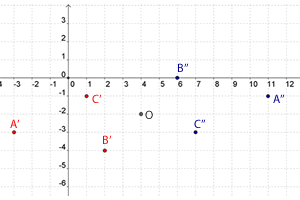
2Calcular los simétricos de los puntos  respecto del origen.
respecto del origen.
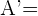 ,
, 
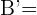 ,
, 
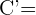 ,
, 
Calcular los simétricos de los puntos  ,
,  y
y 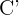 respecto del punto
respecto del punto  .
.
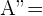 ,
, 
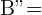 ,
, 
 ,
, 
Cuando nos indican que debemos hallar los puntos simétricos esto significa que debemos hallar los puntos simétricos respecto al origen. Es decir, multiplicamos cada uno de los puntos por  . Por lo tanto los punto simétricos serán,
. Por lo tanto los punto simétricos serán,
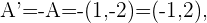
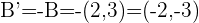
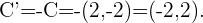
La siguiente figura nos da una descripción graficas de estos puntos.

Para el segundo caso, tenemos que hallar los punto simétricos de  ,
,  y
y 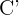 con respecto a
con respecto a 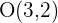 . Para esto debemos trazar un plano sobre el punto
. Para esto debemos trazar un plano sobre el punto  y hallar la simetría en este plano. Con esta idea en mente tenemos que nuestros puntos simétricos estan dados por
y hallar la simetría en este plano. Con esta idea en mente tenemos que nuestros puntos simétricos estan dados por
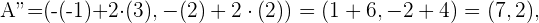
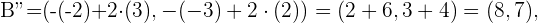
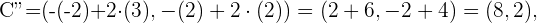
La siguiente figura nos da una descripción graficas de estos puntos.
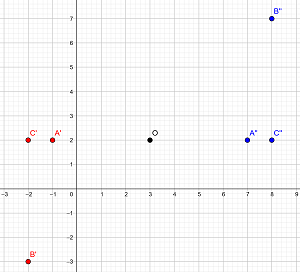
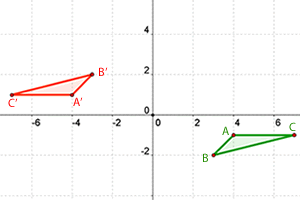
3Dado el triángulo 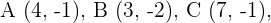 hallar el triángulo simétrico respecto del origen de coordenadas.
hallar el triángulo simétrico respecto del origen de coordenadas.
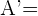 ,
, 
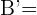 ,
, 
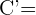 ,
, 
Notemos que estos tres punto nos forma un triángulo y al hallar los punto simétricos obtendremos el triángulo simétrico. Dado que son punto simétricos respecto al origen entonces tenemos que sus puntos simétricos no son mas que los punto con coordenadas opuestas de los punto originalmente dados,
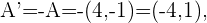


La siguiente figura nos indica el nuevo triángulo simétrico al original.
4Dado el cuadrado de vértices  hallar el cuadrado simétrico respecto del punto
hallar el cuadrado simétrico respecto del punto 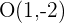 .
.
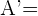 ,
, 
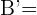 ,
, 
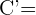 ,
, 
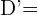 ,
, 
Notemos que estos cuatro punto nos forma un cuadrado y al hallar los punto simétricos obtendremos el cuadrado simétrico. Dado que son punto simétricos respecto al punto 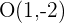 , entonces tenemos que sus puntos simétricos son:
, entonces tenemos que sus puntos simétricos son:
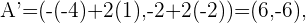
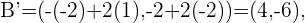
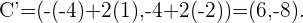
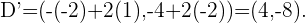
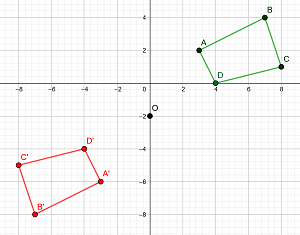
La siguiente figura nos indica el nuevo cuadrado simétrico al original.
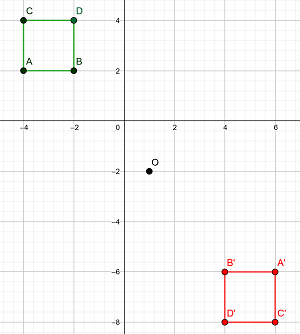
5Dado el cuadrilátero de vértices 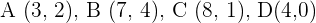 hallar el cuadrilátero simétrico respecto del punto
hallar el cuadrilátero simétrico respecto del punto  .
.
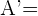 ,
, 
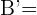 ,
, 
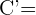 ,
, 
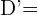 ,
, 
Notemos que estos cuatro punto nos forma un cuadrilátero y al hallar los punto simétricos obtendremos el cuadrilátero simétrico. Dado que son punto simétricos respecto al punto  , entonces tenemos que sus puntos simétricos son:
, entonces tenemos que sus puntos simétricos son:
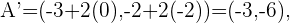

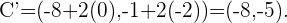
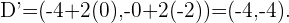
La siguiente figura nos indica el nuevo cuadrilátero simétrico al original.
6Dada la circunferencia de centro 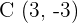 y radio
y radio 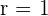 halla su simétrica respecto del origen.
halla su simétrica respecto del origen.
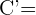 ,
, 
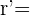
¿Y si calculamos la simétrica de la misma circunferencia respecto del punto 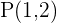 ?
?
 ,
, 
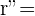
Para hallar la circunferecia simétrica basta con calcular el centro de la nueva circunferencia.
Sabemos que  por tanto el centro simétrico
por tanto el centro simétrico 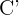 será el punto cuyas coordenadas son las opuestas a las de
será el punto cuyas coordenadas son las opuestas a las de 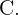 Es decir,
Es decir,
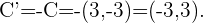
Dado que queremos una circunferencia simétrica, esta solo debe ser opuesta a la original y por lo tanto el radio sigue siendo el mismo, 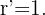
Así que nuestra circunferencia simétrica es aquella de centro en 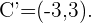 y radio
y radio 
Ahora queremos hallar la circunferencia simétrica respecto del punto 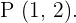
El nuevo centro de la circunferencia será aquel que es simétrico con respecto al plano trazado sobre el punto 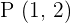 , es decir,
, es decir,
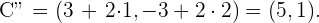
Dado que queremos una circunferencia simétrica, esta debe tener el mismo radio que la original, 
Así que nuestra circunferencia simétrica con respecto a 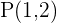 es aquella de centro en
es aquella de centro en 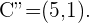 y radio
y radio 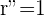
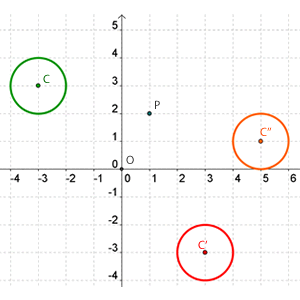
La siguiente figura nos da una descripción grafica del resultado,
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Sean u = 2i − 3j y v = −4i + 6j. Encuentre: 4v − 6u , con su bosquejo
Al trasladar el punto A(2,4) dado el vector B(2-2) se obtiene?
Hola, de la matriz que calcularon la determinante no es =0.
Podrías señalar el ejercicio para rectificar por favor.
Calcular x²+1
Cómo resolver los ejercicios si están en kilómetros por ejemplo:
A= 300km b=4,000km C= 5,000km
Osea cuando sustituimos tenemos que poner √(X1,X2)² + (Y1,X2)²
O (X2,X1)² +(Y2,Y1)²
¿Cual de las dos?
Depende de que quieras obtener y que significa la expresión (X1,X2), la expresión √(X1,X2)² + (Y1,X2)² esta mal escrita si quieres encontrar una distancia.
24 4 70 NE
Vectores modelo