Calcula las coordenadas de los puntos que se obtienen de aplicar las traslaciones indicadas en cada caso, teniendo: 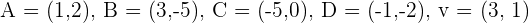 .
.
1
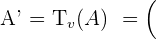 ,
, 
1Llamamos al punto trasladado 
2hay que calcular 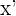 e
e 
3Para calcular 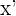 sumamos las primeras coordenadas de
sumamos las primeras coordenadas de 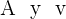
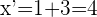
4Para calcular  sumamos las segundas coordenadas de
sumamos las segundas coordenadas de 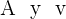
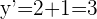
5Así, 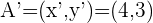
2
 ,
, 
1Llamamos al punto trasladado 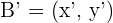
2hay que calcular 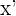 e
e 
3Para calcular 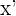 sumamos las primeras coordenadas de
sumamos las primeras coordenadas de 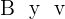
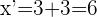
4Para calcular  sumamos las segundas coordenadas de
sumamos las segundas coordenadas de 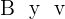

5Así, 
3
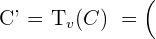 ,
, 
1Llamamos al punto trasladado 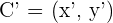
2hay que calcular 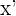 e
e 
3Para calcular 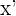 sumamos las primeras coordenadas de
sumamos las primeras coordenadas de 
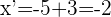
4Para calcular  sumamos las segundas coordenadas de
sumamos las segundas coordenadas de 

5Así, 
4
 ,
, 
1Llamamos al punto trasladado 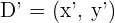
2hay que calcular 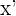 e
e 
3Para calcular 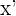 sumamos las primeras coordenadas de
sumamos las primeras coordenadas de 
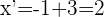
4Para calcular  sumamos las segundas coordenadas de
sumamos las segundas coordenadas de 
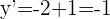
5Así, 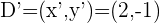
Resuelve los siguientes ejercicios traslaciones
5En una traslación mediante el vector  , un punto
, un punto 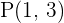 se transforma en
se transforma en  . Calcular el transformado del punto
. Calcular el transformado del punto 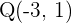 y la transformada de la circunferencia de centro
y la transformada de la circunferencia de centro 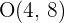 y radio 2.
y radio 2.
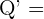 ,
, 
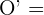 ,
, 
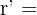
1En primer lugar calculamos las componentes del vector  a partir de los puntos
a partir de los puntos 

2Calculamos el transformado del punto 
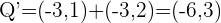
3Calculamos la transformada del centro de la circunferencia
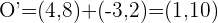
4El radio de la circunferencia no varía, 

6Calcular el transformado del triángulo de vértices 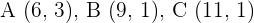 mediante el vector
mediante el vector  .
.
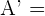 ,
, 
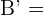 ,
, 
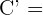 ,
, 
1Transformamos mediante el vector dado cada vértice, así obtendremos el nuevo triángulo
2Encontramos 
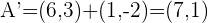
3Encontramos 
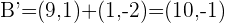
4Encontramos 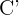

Si tienes dudas puedes consultar la teoría



Sean u = 2i − 3j y v = −4i + 6j. Encuentre: 4v − 6u , con su bosquejo
Al trasladar el punto A(2,4) dado el vector B(2-2) se obtiene?
Hola, de la matriz que calcularon la determinante no es =0.
Podrías señalar el ejercicio para rectificar por favor.
Calcular x²+1
Cómo resolver los ejercicios si están en kilómetros por ejemplo:
A= 300km b=4,000km C= 5,000km
Osea cuando sustituimos tenemos que poner √(X1,X2)² + (Y1,X2)²
O (X2,X1)² +(Y2,Y1)²
¿Cual de las dos?
Depende de que quieras obtener y que significa la expresión (X1,X2), la expresión √(X1,X2)² + (Y1,X2)² esta mal escrita si quieres encontrar una distancia.
24 4 70 NE
Vectores modelo