Capítulos
Si tienes un problema con un modelo que tiene condiciones de contorno definidas, pero también quieres que el modelo tenga cierta flexibilidad para que pueda ser resuelto más fácilmente por diferentes métodos, debes saber qué es un producto escalar.
Puede que no siempre entiendas lo que es un producto escalar, ya que la definición suele implicar complejas ecuaciones matemáticas, pero siguen siendo importantes para entender otros conceptos de la física. En particular, cuando se estudian las condiciones de contorno en la atmósfera, como las nubes de bajo nivel o los chubascos, la inclusión de un producto escalar en la formulación facilitará la resolución del problema.
Un producto escalar es una cantidad escalar o vectorial que tiene un valor definido positivo, pero que no es necesariamente cero. En otras palabras, representa un cambio de cualquier cantidad medible, como un vector, y no necesariamente la posición o dirección real a la que apunta el vector. Los productos escalares de dos o más vectores suelen definirse como la suma de todas las cantidades vectoriales correspondientes, aunque no es necesario.
El producto escalar de dos vectores es una operación que toma dos vectores y produce un número real:
Observemos que el producto escalar se suele denotar por medio de un punto 
. Otra notación que se suele utilizar es 
. Sin embargo, en Superprof siempre denotaremos el producto escalar utilizando un punto.
Además, el producto escalar no debe confundirse con la multiplicación de un vector por un escalar.
Maneras de calcular el producto escalar
Existen dos maneras equivalentes de obtener el producto escalar de dos vectores 
y 
. Estas se describen a continuación:
1 Si conocemos el módulo de ambos vectores y el ángulo 
que forman entre ellos, entonces el producto escalar se obtiene mediante
2 Si conocemos los componentes de los vectores 
y 
, entonces el producto escalar está dado por
Ejemplos
1 Consideremos los vectores 
y 
. Asimismo, el ángulo entre los vectores es 
.
Para calcular el producto escalar, primero debemos encontrar el módulo de y :
De este modo, el producto escalar está dado por
2 Repetiremos el ejemplo anterior con y . Sin embargo, ahora utilizaremos la otra fórmula:
Notemos que el resultado fue el mismo sin importar la fórmula que utilizáramos.
Cálculo del módulo y ángulos de vectores
Como vimos anteriormente, existen dos fórmulas equivalentes para calcular el producto escalar de dos vectores. Por lo tanto, se puede utilizar el producto escalar para calcular el módulo de un vector o el ángulo entre dos vectores.
Calcular el módulo de un vector utilizando el producto escalar
Notemos que si es un vector, entonces
Por lo tanto,
Esta fórmula se puede utilizar para calcular el módulo de un vector utilizando el producto escalar de consigo mismo.
Calcular el ángulo entre dos vectores utilizando el producto escalar
Supongamos que tenemos los vectores y . Entonces
Despejando 
, tenemos
Así, si sustituimos la otra fórmula del producto escalar, se tiene
Esta fórmula se utiliza para calcular utilizando la función arco-coseno.
Ejemplos
1 Consideremos, nuevamente, los vectores y . Entonces el módulo de estos vectores es:
2 Ahora calcularemos el ángulo entre y . Tenemos que
De manera que
Por lo tanto, debemos tener que
Ortogonalidad de dos vectores
Sabemos que dos vectores son ortogonales (o perpendiculares) si el ángulo entre ellos es 
o 
. En cualquiera de estos casos, tenemos que 
. Por lo tanto, si dos vectores son ortogonales, se tiene que
Es decir, dos vectores 
y 
serán ortogonales siempre que se cumpla que
Ejemplo
Verificaremos la ortogonalidad de los vectores y que utilizamos en los ejemplos anteriores. Observemos que
Por lo tanto, los vectores y no son perpendiculares.
Interpretación geométrica del producto escalar
Notemos que 
se puede ver como el módulo de la proyección del vector sobre —siempre que 
—, tal y como se muestra en la siguiente figura. La proyección sería el vector con origen 
y extremo 
.
Eso se sigue al observar el triángulo rectángulo que se formó en la figura anterior. Sabemos que
De manera que, al despejar 
, tenemos
Para imaginar la proyección, piensa que hay una fuente de luz y la proyección es la sombra del vector sobre el vector . Además, esta fuente de luz debe estar colocada de tal forma que un vector perpendicular a no proyecte sombra alguna. Observa la siguiente figura:
De este modo, el producto 
puede verse como el módulo de uno de los vectores multiplicado por el módulo de la proyección del otro vector. Es decir, al sustituir 
en la fórmula del producto escalar, tenemos
Por lo tanto, podemos calcular el módulo de la proyección del vector sobre el vector utilizando
Nota: Si tenemos que es negativo, entonces esto significa que la proyección tiene sentido contrario al vector . Esto ocurre cuando 
o 
. En este caso, el módulo de la proyección está dada por 
. Observa la siguiente figura:
Ejemplo
Encontraremos la proyección de 
sobre el vector 
. Para hacer esto, calculemos
Observemos que 
tiene signo negativo. Por lo tanto, la proyección tiene sentido contrario que y su módulo es 
. Observa la siguiente figura:
Propiedades del producto escalar
El producto escalar satisface diferentes propiedades. Las más importantes son las siguientes:
1 El producto escalar es conmutativo. En otras palabras, "el orden de los factores no altera el producto". De este modo, no importa en qué orden se multipliquen los vectores.
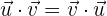
2 Asociatividad respecto a la multiplicación por escalar. Es decir, si multiplicamos por y luego por un escalar 
, entonces el resultado es lo mismo que realizar primero 
y luego hacer el producto escalar por . Esto es,
3 Distributividad respecto a la suma. Esto es,
Nota: Las propiedades 2 y 3 juntas se conocen como linealidad del producto escalar respecto al primer operando.
Nota: Debido a que el producto escalar es conmutativo, entonces también se cumple la linealidad respecto al segundo operando. Es decir,
4 El producto escalar es definido positivo. Esto es, el producto escalar de un vector no nulo por sí mismo siempre es positivo.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Suma de vectores f1=450n,30. 1FR=f1+f6
como sacar el residuo de una multiplicación
Hallar las coordenadas de punto medio del segmento que une (4,7);(14,12)
Hola, podrias mencionar que tipo de multiplicación (normal, de vectores etc.).
si se aplica una traslación al punto E(0;2) se obtiene el punto E'(-1;-5),indicar el vector de translación
Vectores 400n+horizontal y a la izquierda
Cuál es la fuerza resultante de la magnitud , si f1 es 40 newton y 90 grados y f2 es 30 newton y 0 grados?
23
Mi casa se encuentra ubicada en el punto M(8, 3) y la escuela donde estudio se encuentra ubicada en N(-5, 7). ¿Cuál es la distancia entre mi casa (M) y la Escuela (N)