Elige la opción correcta en cada caso:
1Calcula la ecuación vectorial de la recta r que pasa por los puntos A (−1, 0) y B (3, −4)
Para calcular la ecuación vectorial necesitamos un punto y un vector director de la recta.
Podemos elegir cualquiera de los dos puntos, por ejemplo, el (−1, 0). El vector director lo calculamos a partir de los dos puntos por los que pasa la recta:

Entonces la ecuación vectorial es
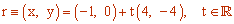
2Calcula la ecuación paramétrica de la recta r que pasa por los puntos A (3, 1) y B (−2, 3)
Para calcular la ecuación paramétrica necesitamos un punto y un vector director de la recta.
Podemos elegir cualquiera de los dos puntos, por ejemplo, el (3, 1). El vector director lo calculamos a partir de los dos puntos por los que pasa la recta:

Entonces la ecuación paramétrica es:
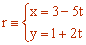
3Calcula la ecuación punto-pendiente de la recta r ≡ 4x − 2y + 6 = 0
Para calcular la ecuación punto-pendiente de la recta necesitamos un punto y la pendiente de la recta.
Para hallar un punto de la recta damos un valor cualquiera a la x y despejamos la y:
Tomamos x = 0 ⇒ 0 − 2y + 6 = 0 ⇒ 2y = 6 ⇒ y = 3
Entonces (0, 3) es un punto de la recta r.
El vector director de la recta viene dado por 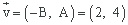
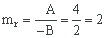
Sustituyendo el punto y la pendiente en la ecuación punto-pendiente de la recta tenemos:
r ≡ y − 3 = 2 (x − 0)
4Calcula la ecuación vectorial de la recta r ≡ y = 5x − 3
Para calcular la ecuación vectorial de la recta necesitamos un punto y el vector director de la recta.
Pasamos primero la recta a forma general:
5x − y − 3 = 0
Para hallar un punto de la recta damos un valor cualquiera a la x y despejamos la y:
Tomamos x = 1 ⇒ 5 − y − 3 = 0 ⇒ y = 2
Entonces (1, 2) es un punto de la recta r.
El vector director de la recta viene dado por 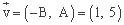
Sustituyendo el punto y el vector director en la ecuación vectorial de la recta queda la ecuación pedida:
r ≡ (x, y) = (1, 2) + t (1, 5), t ∈ 
5Calcula la ecuación punto-pendiente de la recta 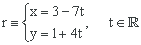
Para calcular la ecuación punto-pendiente necesitamos un punto y la pendiente de la recta.
A partir de las ecuaciones paramétricas de la recta, obtenemos un punto por el que pasa la recta, (3, 1), y el vector director 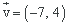
De aquí la pendiente es 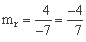
Luego la ecuación pedida es:
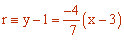
6Calcula la ecuación segmentaria o canónica de la recta 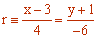
Empezamos pasando la recta a forma general:
−6(x − 3) = 4(y + 1)
−6x + 18 = 4y + 4
r ≡ 6x + 4y − 14 = 0
Pasamos el término independiente al otro lado de la igualdad:
6x + 4y = 14
Dividimos ambos términos de la igualdad por el término independiente para que el término independiente sea 1.
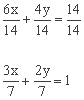
Operando obtenemos la ecuación pedida:
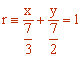
7Calcula la ecuación vectorial de la recta r ≡ y + 2 = −4(x − 1)
Empezamos pasando la recta a forma general:
y + 2 = −4x + 4
y + 4x − 2 = 0
Para calcular la ecuación vectorial necesitamos un punto y el vector director de la recta.
Para hallar un punto de la recta damos un valor cualquiera a la x y despejamos la y:
Tomamos x = 1 ⇒ y + 4 − 2 = 0 ⇒ y = −2
Entonces (1, −2) es un punto de la recta r.
El vector director de la recta viene dado por 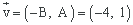
Sustituyendo el punto y el vector director en la ecuación vectorial de la recta queda la ecuación pedida:
r ≡ (1, −2) + t (−4, 1), t ∈ 
8Calcula la ecuación paramétrica de la recta r ≡ 2x − 7y − 3 = 0
Para calcular la ecuación paramétrica necesitamos un punto y el vector director de la recta.
Para hallar un punto de la recta damos un valor cualquiera a la x y despejamos la y:
Tomamos x = 0 ⇒ 7y = −3 ⇒ 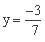
Entonces 
El vector director de la recta viene dado por 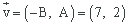
Sustituyendo el punto y el vector director en la ecuación paramétrica de la recta queda la ecuación pedida:

Si tienes dudas puedes consultar la teoría



encuentre una forma general de una ecuación de la recta q pasa por el punto A q satisfaga la condicion dada A (5, – 2)
a) paralelo al eje y
b) perpendicular al eje y
¿Cuál es el lugar geométrico descrito por la trayectoria de un avión que se mantiene sobre volando la ciudad de San José a una distancia constante de 5 km de la Torre de Juan Santamaría
Graficar y calcular la distancia y punto Medio de los siguientes P(1,1),Q (3,3)
Hallar la distancia y la pendiente de A(07)
B(2,1)
F(×)=5-2×
A= (7,7)
B= (-9,-6)
Ecuación explícita de la recta
una recta pasa por el punto (0,-5) formando con una x un ángulo de x=90° Hallar la ecuación de la recta
1. Hallar las ecuaciones paramétricas de la recta que pasa por A(3,-1,0) y su vector director sea
perpendicular a los vectores: w = y u =