Temas

¿Qué es la ecuación canónica o segmentaria?
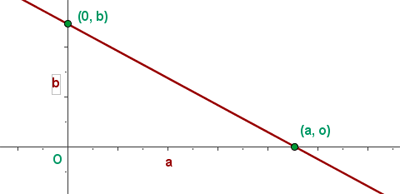
La ecuación canónica o segmentaria de la recta, es la expresión algebraica de la recta que se determina conociendo a los valores dónde la recta corta a cada uno de los ejes coordenados.
El valor donde la recta corta al eje  le llamaremos
le llamaremos  , y el valor donde la recta corta al eje
, y el valor donde la recta corta al eje  le llamaremos
le llamaremos  , generando los dos puntos en el plano cartesiano
, generando los dos puntos en el plano cartesiano  y
y  respectivamente.
respectivamente.
En muchas ocasiones, tenemos la ecuación general de la recta, y partiendo de ahí necesitamos la ecuación canónica, por esta razón veamos el proceso algebraico a seguir, para que también de esta manera conozcamos la estructura de la ecuación canónica de la recta.
Comencemos con le ecuación general de la recta.
Ecuación general de la recta

Ecuación canónica a partir de la ecuación general de la recta
Sabiendo que la ecuación general de la recta es:

Suponemos que  con la finalidad de saber el lugar donde la recta corta al eje
con la finalidad de saber el lugar donde la recta corta al eje  , entonces la ecuación general queda:
, entonces la ecuación general queda:
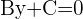
despejamos a  ,
,
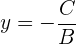
El valor encontrado corresponde a  , de la ecuación canónica
, de la ecuación canónica

y usando el mismo razonamiento podemos conocer al valor  , de la ecuación canónica
, de la ecuación canónica
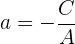
Resumen del proceso para encontrar la ecuación canónica
Si la ecuación general de la recta es:

Entonces,
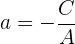

y así la forma que tiene la ecuación canónica es
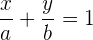
Ya que, si partimos de la forma general

y movemos del otro lado de la igualdad al independiente
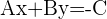
y luego dividimos entre 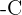 (el cual debe de ser distinto de cero) tenemos
(el cual debe de ser distinto de cero) tenemos
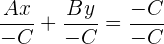
llegamos a que

y entonces, así es como queda la ecuación canónica de la recta
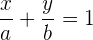
Donde
 es la abscisa en el origen de la recta.
es la abscisa en el origen de la recta. es la ordenada en el origen de la recta.
es la ordenada en el origen de la recta.- El independiente de la general NO debe ser cero, significa que la forma canónica de la recta NO describe a las rectas que pasan por el origen, ya que ahí
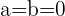
- Si
 o
o  de la ecuación general son cero, significa que la recta es horizontal o vertical respectivamente, lo que lleva a que
de la ecuación general son cero, significa que la recta es horizontal o vertical respectivamente, lo que lleva a que  o
o  de la ecuación canónica no existen, entonces tampoco hay forma de la ecuación canónica para este caso.
de la ecuación canónica no existen, entonces tampoco hay forma de la ecuación canónica para este caso.
Fórmula de la ecuación canónica
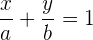
Ejemplos de problemas con la ecuación canónica
1 Una recta determina sobre los ejes coordenados, segmentos de  y
y  unidades, respectivamente.Hallar su ecuación.
unidades, respectivamente.Hallar su ecuación.
En este caso es simple, ya que de la información vemos que  y
y  , por lo que solamente es necesario sustituir los valores en la ecuación
, por lo que solamente es necesario sustituir los valores en la ecuación
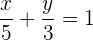
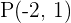 y tiene por vector director
y tiene por vector director  .
.
Observamos que por la información que nos presentan, es conveniente ocupar la ecuación de la recta en su forma continua, para esto recordemos un poco de su estructura.
Si tenemos
- Un punto por donde pasa la recta
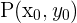
- Un vector director
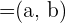 .
.
entonces la ecuación de la recta en su forma continua es
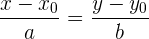 .
.
Con esto, podemos hallar la ecuación en forma continua:
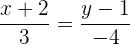 .
.
y con esta ecuación ya podemos transformarla en la forma de la ecuación canónica.
Primero pasamos a la general, y de ahí obtenemos los valores de  y
y  :
:
Movemos los denominadores multiplicando al otro lado de la igualdad
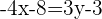
movemos a las expresiones de un solo lado de la igualdad, escribiendo la forma de la ecuación general
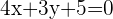
observamos que el independiente  y los valores
y los valores  y
y  de la general son distintos de cero.
de la general son distintos de cero.
Entonces ya podemos calcular a la forma canónica de la recta donde  y
y 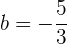 , llegando a que
, llegando a que

Por otro lado, comentemos que la ecuación de la recta en su forma canónica nos brinda la información necesaria para poder realizar otros cálculos, por ejemplo de la recta  que forma un triángulo con los ejes, podemos calcular dicha área.
que forma un triángulo con los ejes, podemos calcular dicha área.
Veamos, la recta forma un triángulo rectángulo con el origen y sus catetos son la abscisa y la ordenada en el origen, en otras palabras, los valores de a y b de la forma canónica
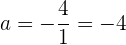

Entonces la ecuación canónica es:
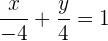
y entonces el área es:
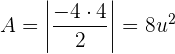
ocuparemos este resultado para nuestro siguiente ejercicio.
3 Una recta pasa por el punto 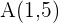 y determina con los ejes de coordenadas un triángulo de
y determina con los ejes de coordenadas un triángulo de 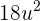 de superficie. ¿Cuál es la ecuación de la recta?
de superficie. ¿Cuál es la ecuación de la recta?
Aplicamos  ,
, 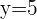 a la ecuación canónica:
a la ecuación canónica:

por otro lado el área del triángulo que genera la recta con los ejes es:
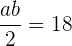
generándose así un sistema de ecuaciones (dos ecuaciones dos incógnitas)
Resolvemos el sistema:
Si en la primer ecuación multiplicamos por 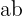 y en la segunda por
y en la segunda por  , se forma el siguiente sistema
, se forma el siguiente sistema
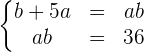
Para resolverlo, multiplicamos a ambas ecuaciones por a
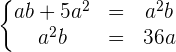
luego sustituimos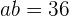 ,
, 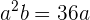 en la ecuación
en la ecuación 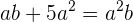 y llegamos a la siguiente ecuación de segundo grado
y llegamos a la siguiente ecuación de segundo grado 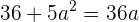 , que acomodándola queda
, que acomodándola queda 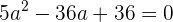 .
.
Resolviendo a la ecuación de segundo grado, llegamos a que se tienen dos soluciones reales (hay dos rectas que cumplen la condición)
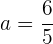 y
y 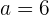
entonces para saber el valor de  , ocupamos el despeje de una igualdad, es decir
, ocupamos el despeje de una igualdad, es decir 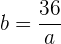
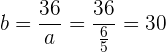 y
y 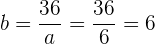
Significa que las dos ecuaciones de las rectas que cumplen la condición son
 y
y 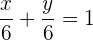
4 Sabemos que una recta pasa por el punto  y que determina sobre los ejes coordenados, segmentos de doble longitud en el eje de abscisas, que en el de ordenadas. Hallar la ecuación de esta recta.
y que determina sobre los ejes coordenados, segmentos de doble longitud en el eje de abscisas, que en el de ordenadas. Hallar la ecuación de esta recta.
La gráfica representa la situación del problema
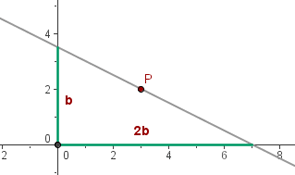
entonces podemos sustituir los valores en la ecuación de forma canónica
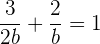
multiplicando todo por  nos lleva a que
nos lleva a que
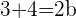
significa que
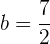
entonces
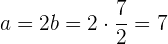
quedando así la ecuación buscada
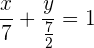













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
¿Cuál es el lugar geométrico descrito por la trayectoria de un avión que se mantiene sobre volando la ciudad de San José a una distancia constante de 5 km de la Torre de Juan Santamaría
Graficar y calcular la distancia y punto Medio de los siguientes P(1,1),Q (3,3)
Hallar la distancia y la pendiente de A(07)
B(2,1)
F(×)=5-2×
A= (7,7)
B= (-9,-6)
Ecuación explícita de la recta
una recta pasa por el punto (0,-5) formando con una x un ángulo de x=90° Hallar la ecuación de la recta
1. Hallar las ecuaciones paramétricas de la recta que pasa por A(3,-1,0) y su vector director sea
perpendicular a los vectores: w = y u =
Cuál es la recta que contiene a los puntos o(-2,1) y Q(-3,-4)