Elige la opción correcta en cada caso:
1Calcula la ecuación vectorial de la recta r que pasa por los puntos A (−1, 0) y B (3, −4)
Para calcular la ecuación vectorial necesitamos un punto y un vector director de la recta.
Podemos elegir cualquiera de los dos puntos, por ejemplo, el (−1, 0). El vector director lo calculamos a partir de los dos puntos por los que pasa la recta:

Entonces la ecuación vectorial es
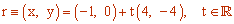
2Calcula la ecuación paramétrica de la recta r que pasa por los puntos A (3, 1) y B (−2, 3)
Para calcular la ecuación paramétrica necesitamos un punto y un vector director de la recta.
Podemos elegir cualquiera de los dos puntos, por ejemplo, el (3, 1). El vector director lo calculamos a partir de los dos puntos por los que pasa la recta:

Entonces la ecuación paramétrica es:
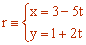
3Calcula la ecuación punto-pendiente de la recta r ≡ 4x − 2y + 6 = 0
Para calcular la ecuación punto-pendiente de la recta necesitamos un punto y la pendiente de la recta.
Para hallar un punto de la recta damos un valor cualquiera a la x y despejamos la y:
Tomamos x = 0 ⇒ 0 − 2y + 6 = 0 ⇒ 2y = 6 ⇒ y = 3
Entonces (0, 3) es un punto de la recta r.
El vector director de la recta viene dado por 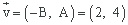
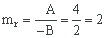
Sustituyendo el punto y la pendiente en la ecuación punto-pendiente de la recta tenemos:
r ≡ y − 3 = 2 (x − 0)
4Calcula la ecuación vectorial de la recta r ≡ y = 5x − 3
Para calcular la ecuación vectorial de la recta necesitamos un punto y el vector director de la recta.
Pasamos primero la recta a forma general:
5x − y − 3 = 0
Para hallar un punto de la recta damos un valor cualquiera a la x y despejamos la y:
Tomamos x = 1 ⇒ 5 − y − 3 = 0 ⇒ y = 2
Entonces (1, 2) es un punto de la recta r.
El vector director de la recta viene dado por 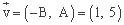
Sustituyendo el punto y el vector director en la ecuación vectorial de la recta queda la ecuación pedida:
r ≡ (x, y) = (1, 2) + t (1, 5), t ∈ 
5Calcula la ecuación punto-pendiente de la recta 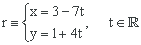
Para calcular la ecuación punto-pendiente necesitamos un punto y la pendiente de la recta.
A partir de las ecuaciones paramétricas de la recta, obtenemos un punto por el que pasa la recta, (3, 1), y el vector director 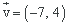
De aquí la pendiente es 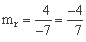
Luego la ecuación pedida es:
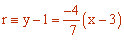
6Calcula la ecuación segmentaria o canónica de la recta 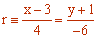
Empezamos pasando la recta a forma general:
−6(x − 3) = 4(y + 1)
−6x + 18 = 4y + 4
r ≡ 6x + 4y − 14 = 0
Pasamos el término independiente al otro lado de la igualdad:
6x + 4y = 14
Dividimos ambos términos de la igualdad por el término independiente para que el término independiente sea 1.
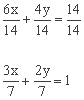
Operando obtenemos la ecuación pedida:
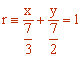
7Calcula la ecuación vectorial de la recta r ≡ y + 2 = −4(x − 1)
Empezamos pasando la recta a forma general:
y + 2 = −4x + 4
y + 4x − 2 = 0
Para calcular la ecuación vectorial necesitamos un punto y el vector director de la recta.
Para hallar un punto de la recta damos un valor cualquiera a la x y despejamos la y:
Tomamos x = 1 ⇒ y + 4 − 2 = 0 ⇒ y = −2
Entonces (1, −2) es un punto de la recta r.
El vector director de la recta viene dado por 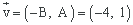
Sustituyendo el punto y el vector director en la ecuación vectorial de la recta queda la ecuación pedida:
r ≡ (1, −2) + t (−4, 1), t ∈ 
8Calcula la ecuación paramétrica de la recta r ≡ 2x − 7y − 3 = 0
Para calcular la ecuación paramétrica necesitamos un punto y el vector director de la recta.
Para hallar un punto de la recta damos un valor cualquiera a la x y despejamos la y:
Tomamos x = 0 ⇒ 7y = −3 ⇒ 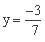
Entonces 
El vector director de la recta viene dado por 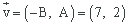
Sustituyendo el punto y el vector director en la ecuación paramétrica de la recta queda la ecuación pedida:

Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Alguien me puede ayudar por favor necesito dar un examen para repasar y no me salen las respuestas
Hola con gusto te ayudamos, podrías mencionar específicamente con cual ejercicio podemos darte una mejor explicación.
Determinar las ecuaciones parametricas del plano x-2y+z-1=0
Hola, me sirvio mucho, con que informacion podria ponerlos como refernecia en mi proyecto?
Hola que bueno que la pagina te ayudo, podrías poner como pagina de internet «Materíal didactico-Superprof».
– Hallar la ecuación de la recta en su forma simétrica que tiene pendiente igual a 3/2 y que intersecta al eje «y» en (0.2)
Buenas tardes,
Me han ayudado muchísimo vuestros apuntes. Sólo tengo una consulta, ¿cómo tendría que calcular la pendiente de una recta en 3 dimensiones, es decir, en el espacio cartesiano (x, y, z)?
En tres dimensiones no se usa la pendiente pues como se usan tres ejes todo cambia, sino más bien el ángulo que se calcula con el vector director de la recta.