Resuelve los siguientes problemas:
1 Calcula el volumen de papel higiénico que hay en el siguiente rollo. Redondea a dos cifras decimales.

V = cm³
En primer lugar observemos que debemos calcular dos volúmenes. El volumen del cilindro formado por el papel y el volumen del cilindro hueco que aparece en el interior.
Una vez hecho esto deberemos restar el segundo al primero para calcular el volumen exacto de papel higiénico de que disponemos.

Como el diámetro mide  cm, el radio será de
cm, el radio será de  cm.
cm.
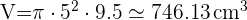

Como el diámetro mide  cm, el radio será de
cm, el radio será de  cm.
cm.



2 Volumen y área cilindro circunscrito en un prisma hexagonal de base un hexágono regular cuya apotema es de 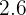 cm y altura de
cm y altura de  cm. Redondea a dos cifras decimales.
cm. Redondea a dos cifras decimales.

A = cm²
V = cm³
Para calcular el área y el volumen del cilindro necesitamos la altura (ya la tenemos) y el radio que obtenemos aplicando Pitágoras.

3 Calcular la altura de un cono de helado cuyo diámetro mide  cm y su volumen es de
cm y su volumen es de 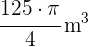 . Redondea a dos cifras decimales.
. Redondea a dos cifras decimales.

h = cm
Si en vez de colocar una sola bola de helado en el cono, lo llenásemos entero, ¿qué volumen de helado necesitaríamos?
V = cm³
Para no mancharnos el cono se envuelve con un papel con la misma forma pero con 3 cm menos de altura. ¿Qué cantidad de papel es la que usamos?
A = cm²

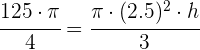
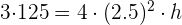
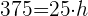


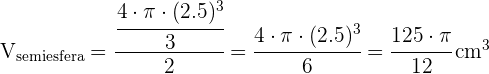
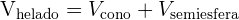
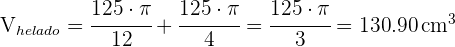

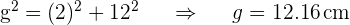
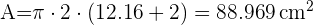
4 En un cubo de volumen un metro cúbico introducimos un cono cuya base está marcada por la circunferencia inscrita a la base del cubo. Si llenamos de agua el espacio que queda libre en el cubo, ¿qué volumen de agua necesitaríamos? Redondea a dos cifras decimales.

V = cm³
Para saber el volumen de agua necesario basta con calcular el volumen del cono y restarlo al volumen del cubo. La altura del cono es de  m y el radio mide
m y el radio mide  m ya que la base del mismo es la circunferencia inscrita en la base del cubo. La generatriz la obtenemos por Pitágoras a partir del radio y de la altura.
m ya que la base del mismo es la circunferencia inscrita en la base del cubo. La generatriz la obtenemos por Pitágoras a partir del radio y de la altura.

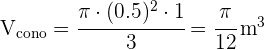
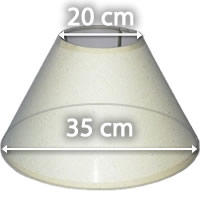
5 ¿Qué cantidad de plástico se ha necesitado para construir la pantalla de la siguiente lámpara cuya altura mide  cm?. Redondea a dos cifras decimales.
cm?. Redondea a dos cifras decimales.
A = cm²
¿Qué volumen ocuparía dicha pantalla si fuese sólida?
V = cm³
Para calcular la cantidad de plástico necesario calculamos el área lateral de la pantalla que es un tronco de cono
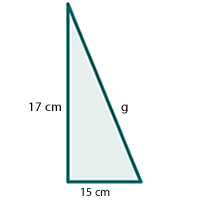
En primer lugar calculamos la generatriz del cono por Pitágoras:


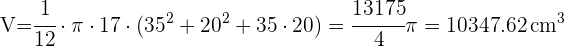
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Un cilindro tiene por altura la misma longitud que la circunferencia de la base. Y la altura mide 130 cm. Calcular: A El área total. B El volumen
cuantas medidas de diámetro y altura se deben efectuar para determinar el volumen de un cilindro con un error no mayor al 0.1%. Una medida del diámetro y altura son respectivamente 13,33 cm y 7,65 cm. Emplee la probabilidad dem 95%
Me pueden ayudar con ese ejercicio por favor
Cuál es el volumen de un prisma trapezoidal (4 caras son trapecios) con dos bases rectangulares?
Hola buenas. En el ejercicio 20 (el de la cúpula) se trata el diámetro de la semiesfera (50) como el radio. La fórmula nos dice que es (en el caso de la semiesfera) = 2 π * r². Pero en el solucionaro está puesto como 50
Un cilindro de gas de 48cm de h con un diametro de 20cm porfavor…… Ayudaaa
Una disculpa ya se corrigió.
Calcular la superficie y el volumen de la siguiente pirámide de apotema 8,6 cm y apotema
de la base de 2,4 cm. (Todas las medidas están en cm).
Una persona busca asesoramiento para garantizar el cuidado de una pileta.
Le indican que por cada m3 de volumen debe agregar 1 litro de producto A que viene en
presentación de galones
¿¿Si la pileta tiene 74 m3 cuantos galones deben comprarse??
cono con radio de 4 cm y altura de 7 cm