Atendiendo al siguiente dibujo escoge la opción correcta:
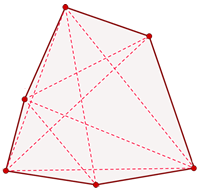
1Los segmentos del contorno del polígono se denominan ...
2Los puntos señalan...
3En el dibujo...
4La suma de los ángulos interiores de este polígono es de...
Elige la opción correcta:
5Un polígono tiene...
6Un polígono...
7Los ángulos interiores de un polígono de 5 lados suman...
8Un polígono de 7 lados tiene...
Responde a las siguientes cuestiones:
9Sabiendo que la suma de los ángulos interiores de cierto polígono es de 720°, ¿cuántos lados tiene dicho polígono?
720 : 180 = 4
Entonces, el número por el que multiplicamos 180° será 4. Si miramos en la fórmula ese número es igual a n − 2, donde n es el número de lados del polígono.
Probando es fácil llegar a que el número de lados es n = 6
El polígono tiene 6 lados.
10Ana ha dibujado un polígono de 10 lados y ha conseguido trazar 28 diagonales de todas las que tiene. ¿Sabrías decir cuántas le faltan por trazar?
Le faltan diagonales.
10 · (10 − 3) : 2 = 10 · 7 : 2 = 70 : 2 = 35
35 − 28 = 7
Le faltan 7 diagonales por trazar.
11¿Existe algún polígono tal que la suma de sus ángulos interiores sea igual a 920°? (Sí o No)
La división 920 : 180 no es exacta, de donde, 920 no es divisor de 180. Por tanto, no existe ningún polígono en las condiciones del enunciado.
12Arrastra cada polígono a la medida que se corresponde con el ángulo que le falta:
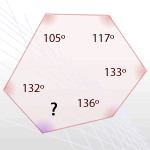

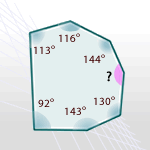
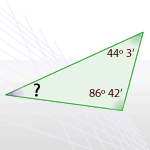
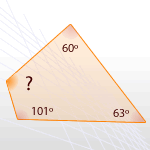
| 136° | 97° | 49° 15' | 162° | 113° | 108° |
 |  |  |  |  |  |
La suma de los ángulos de este polígono es (6 − 2) · 180º = 4 · 180º = 720º
Los ángulos conocidos suman un total de 623º
Por tanto, la medida del ángulo que falta es 720º − 623º = 97º
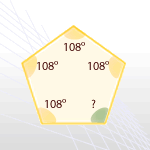
La suma de los ángulos de este polígono es (5 − 2) · 180º = 3 · 180º = 540º
Los ángulos conocidos suman un total de 432º
Por tanto, la medida del ángulo que falta es 540º − 432º = 108º
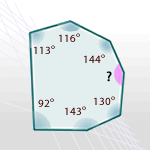
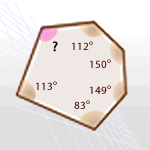
La suma de los ángulos de este polígono es (7 − 2) · 180º = 5 · 180º = 900º
Los ángulos conocidos suman un total de 738º
Por tanto, la medida del ángulo que falta es 900º − 738º = 162º

La suma de los ángulos de este polígono es (3 − 2) · 180º = 1 · 180º = 180º
Los ángulos conocidos suman un total de 130º 45'
Por tanto, la medida del ángulo que falta es 180º − 130º 45' = 49º 15'

La suma de los ángulos de este polígono es (4 − 2) · 180º = 2 · 180º = 360º
Los ángulos conocidos suman un total de 224º
Por tanto, la medida del ángulo que falta es 360º − 224º = 136º
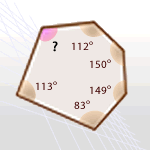
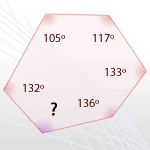
La suma de los ángulos de este polígono es (6 − 2) · 180º = 4 · 180º = 720º
Los ángulos conocidos suman un total de 607º
Por tanto, la medida del ángulo que falta es 720º − 607º = 113º
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Será que me pueden ayudar en este problema de encontrar el cateto ” a” en un triángulo rectángulo donde la hipotenusa mide 4 cm y el cateto “B” mide 3 cm , ayudaaaa
gracias por su tarea
GRACIAS POR SEMEJANTE TRABAJO, CREATIVO Y MUY BIEN ESTRUCTURADOS LOS PROBLEMAS
Quisiera si me pueden ayudar a resolver estos problemas : Hallar el area de la interseccion de los circulos . x2 +y2 = 9 y x2 +y2 =6x y otro es; Hallar la ongitud del arco de la curva a) x = 1/2 y elevado la 2 – i/4 desde y=1 hasta y = e b) (y +1)elevado a la 2 = 4x elevado a la 3 desde (0,,0) hasta (1.5)
longitud y perímetro con los datos r=14.5cm \theta =(3)/(4\pi )
los puntos A, B, C, D, E y F de la circunferencia de centro O y
4cm de radio determinan seis arcos congruentes. Hola profesor, ¿usted me puede ayudar con ese problemas?
El perímetro o longitud de un CD (disco compacto de forma circular) es 42𝜋
2 +8𝜋 − 4 𝑐𝑚, hallar el polinomio
que representa el valor del radio (segmento de recta que va del centro de la circunferencia a cada uno de los
puntos de esta). Teniendo en cuenta que la longitud de la circunferencia (C)= 2π r, por lo tanto se debe despejar
el radio (r).
CUAL ES EL AREA Y EL PERIMETRO DE LA CIRCUNFERENCIA QUE SE ENCUENTRA DENTRO DE UN CUADRADO DE 10 CM DE LADO
el %de 50 de $
Un parque tiene la forma que aparece en la siguiente gráfica.
En el centro hay un lago circular de 18 m de diámetro y en cada uno de los círculos pequeños de 40 dm de radio hay un árbol. El resto del parque corresponde a la zona verde que pueden disfrutar los visitantes. ¿Qué área del parque es zona verde?