1La hipotenusa de un triángulo rectángulo mide 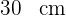 y la proyección de un cateto sobre ella
y la proyección de un cateto sobre ella 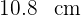 . Hallar el cateto
. Hallar el cateto  .
.
1 Representamos gráficamente el problema
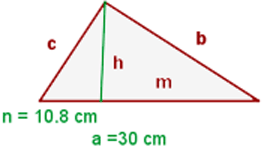
2 Observamos que se obtienen dos triángulos equivalentes por lo que se obtiene

3 Resolviendo para  se tiene
se tiene
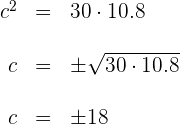
4 Como las distancias no pueden ser negativas, el valor del cateto solicitado es 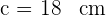
2 En un triángulo rectángulo, las proyecciones de los catetos sobre la hipotenusa miden  y
y  metros. Calcular la altura relativa a la hipotenusa.
metros. Calcular la altura relativa a la hipotenusa.
1 Representamos gráficamente el problema

2 Observamos que se obtienen dos triángulos equivalentes por lo que se obtiene
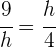
3 Resolviendo para  se tiene
se tiene
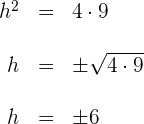
4 Como las distancias no pueden ser negativas, el valor solicitado es 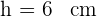
¡No te pierdas nuestras clases particulares de matematicas!
3 La hipotenusa de un triángulo rectángulo mide  y la proyección de un cateto sobre ella
y la proyección de un cateto sobre ella  . Calcular los catetos y la altura relativa a la hipotenusa.
. Calcular los catetos y la altura relativa a la hipotenusa.
1 Representamos gráficamente el problema
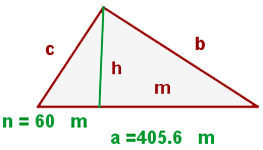
2 Observamos que se obtienen dos triángulos equivalentes, como la hipotenusa es  y la proyección de un cateto es
y la proyección de un cateto es  , tenemos que
, tenemos que
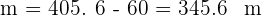
3 Para el cateto  se tiene
se tiene
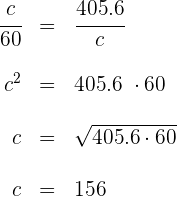
4 Para el cateto  se tiene
se tiene
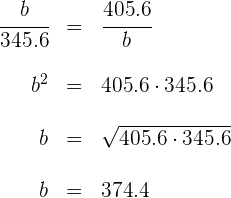
5 Para la altura  relativa a la hipotenusa se tiene
relativa a la hipotenusa se tiene

4 Calcular los lados de un triángulo rectángulo sabiendo que la proyección de uno de los catetos sobre la hipotenusa es  y la altura relativa de la misma
y la altura relativa de la misma 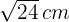 .
.
1 Representamos gráficamente el problema

2 Observamos que se obtienen dos triángulos equivalentes, por lo que tenemos que
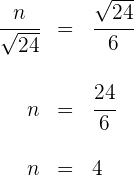
Así, la hipotenusa mide

3 Para el cateto  se tiene
se tiene
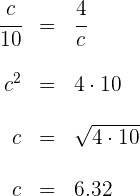
4 Para el cateto  se tiene
se tiene
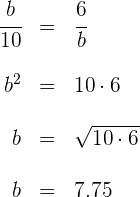
5 Así, los lados del triángulo son: 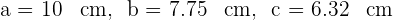
5Una escalera de  de longitud está apoyada sobre la pared. El pie de la escalera dista
de longitud está apoyada sobre la pared. El pie de la escalera dista  de la pared. ¿Qué altura alcanza la escalera sobre la pared?
de la pared. ¿Qué altura alcanza la escalera sobre la pared?
1 Representamos gráficamente el problema
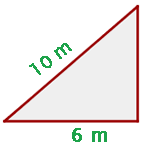
2 Observamos que la altura de la escalera sobre la pared se obtiene con el teorema de Pitágoras
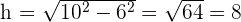
3 Así, la atura solicitada es 
6Determinar el lado de un triángulo equilátero cuyo perímetro es igual al de un cuadrado de 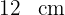 de lado. ¿Serán iguales sus áreas?
de lado. ¿Serán iguales sus áreas?
1Representamos gráficamente el cuadrado

2Su perímetro es  . Para calcular el área empleamos
. Para calcular el área empleamos
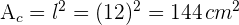
3El triángulo equilátero tiene sus tres lados iguales, por lo que si su perímetro es de 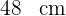 , entonces cada uno de sus lados mide
, entonces cada uno de sus lados mide 

4Para encontrar el área requerimos conocer su altura, para esto dividimos el triángulo equilátero en dos triángulos rectángulos y aplicamos el teorema de Pitágoras

5Para calcular su área, empleamos

Así, ambas figuras tienen el mismo perímetro, pero distinta área.
7Calcular el área de un triángulo equilátero inscrito en una circunferencia de radio  .
.
1Representamos gráficamente el problema
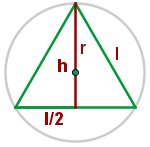
2El centro de la circunferencia es el baricentro, por tanto 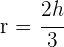 y se obtiene
y se obtiene

3Para encontrar el área del triángulo requerimos conocer su base, para esto dividimos el triángulo equilátero en dos triángulos rectángulos y aplicamos el teorema de Pitágoras
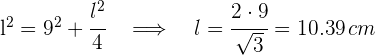
4Para calcular su área, empleamos
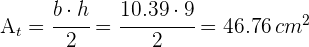
8Determinar el área del cuadrado inscrito en una circunferencia de longitud  .
.
1Representamos gráficamente el problema

2Necesitamos conocer un lado del cuadrado, para esto primero calculamos el radio a partir de conocer la circunferencia
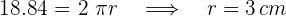
3Para encontrar el lado del cuadrado, consideramos el triángulo rectángulo isósceles cuyos lados iguales son los radios de la circunferencia

4Así, el área del cuadrado es
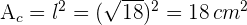
9En un cuadrado de  de lado se inscribe un círculo y en este círculo un cuadrado y en este otro círculo. Hallar el área comprendida entre el último cuadrado y el último círculo.
de lado se inscribe un círculo y en este círculo un cuadrado y en este otro círculo. Hallar el área comprendida entre el último cuadrado y el último círculo.
1Representamos gráficamente el problema
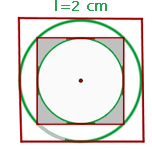
2Necesitamos conocer los radios de los círculos; para esto observamos que el lado del cuadrado de lado  es igual al diámetro del círculo inscrito
es igual al diámetro del círculo inscrito
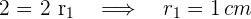
3El díámetro del primer círculo es igual a la diagonal del segundo cuadrado, aplicando e teorema de Pitágoras obtenemos el lado del segundo cuadrado

4Así, el área del segundo cuadrado es
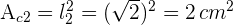
5El diámetro del segundo círculo es igual al lado del segundo cuadrado

6El área el segundo círculo es
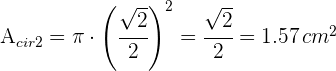
7Así, el área solicitada es
10El perímetro de un trapecio isósceles es de  , las bases miden
, las bases miden  y
y  respectivamente. Calcular los lados no paralelos y el área.
respectivamente. Calcular los lados no paralelos y el área.
1Representamos gráficamente el problema
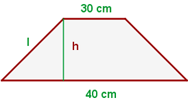
2 Como las bases suman  , entonces los lados suman
, entonces los lados suman  , luego cada lado mide
, luego cada lado mide  . Para conocer la altura construimos un triángulo rectángulo como en la figura. empleando el teorema de Pitágorasse tiene
. Para conocer la altura construimos un triángulo rectángulo como en la figura. empleando el teorema de Pitágorasse tiene

3Calculamos el área del trapecio
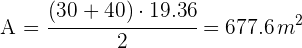
11Si los lados no paralelos de un trapecio isósceles se prolongan, quedaría formado un triángulo equilátero de  de lado. Sabiendo que el trapecio tiene la mitad de la altura del triángulo, calcular el área del trapecio.
de lado. Sabiendo que el trapecio tiene la mitad de la altura del triángulo, calcular el área del trapecio.
1Representamos gráficamente el problema
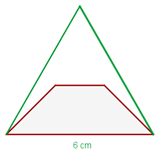
2 Para conocer la altura del triángulo, construimos un triángulo rectángulo cuya base es la mitad de su altura. Empleando el teorema de Pitágoras se tiene
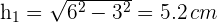
3Calculamos la altura 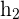 del trapecio
del trapecio
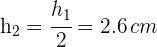
4Calculamos el área del trapecio

12El área de un cuadrado es 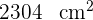 . Calcular el área del hexágono regular que tiene su mismo perímetro.
. Calcular el área del hexágono regular que tiene su mismo perímetro.
1Representamos gráficamente el problema

2 Para conocer el perímetro del cuadrado, debemos calcular el valor de uno de sus lados
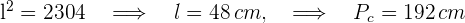
3Calculamos la apotema del hexágono, para ello requerimos el lado del hexágono 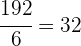
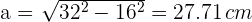
4Calculamos el área del hexágono

13En una circunferencia de radio igual a 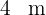 se inscribe un cuadrado y sobre los lados de este y hacia el exterior se construyen triángulos equiláteros. Hallar el área de la estrella así formada.
se inscribe un cuadrado y sobre los lados de este y hacia el exterior se construyen triángulos equiláteros. Hallar el área de la estrella así formada.
1Representamos gráficamente el problema
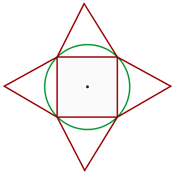
2Necesitamos conocer el lado del cuadrado; para esto observamos que el diámetro de la circunferencia es igual a la diagonal del cuadrado. aplicando el teorema de Pitágoras se obtiene

3El área del cuadrado es

4Para encontrar el área del triángulo equilátero, dividimos en dos triángulos rectángulos y aplicamos el teorema de Pitágoras para encontrar la altura
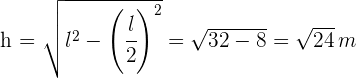
5El área del triángulo es
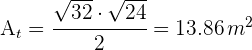
6El área de la estrella es

14A un hexágono regular  de lado se le inscribe una circunferencia y se le circunscribe otra. Hallar el área de la corona circular así formada.
de lado se le inscribe una circunferencia y se le circunscribe otra. Hallar el área de la corona circular así formada.
1Representamos gráficamente

2 Calculamos el radio de la circunferencia circunscrita, para esto observamos que el hexágono se divide en seis triángulos equiláteros iguales, por lo que

3Calculamos el radio de la circunferencia inscrita, este coincide con la altura del triángulo equilátero

4Calculamos el área de la corona circular, la cual se obtiene a partir de la diferencia de áreas de los círculos
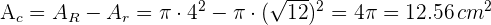
15En una circunferencia una cuerda de 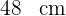 y dista
y dista  del centro. Calcular el área del círculo.
del centro. Calcular el área del círculo.
1Representamos gráficamente

2 Consideramos el triángulo rectángulo como se muestra en la figura y empleando el teorema de Pitágoras, calculamos el radio

3Calculamos el área del círculo
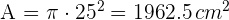
16Los catetos de un triángulo rectángulo inscrito en una circunferencia miden 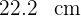 y
y  respectivamente. Calcular el área del círculo.
respectivamente. Calcular el área del círculo.
1Representamos gráficamente
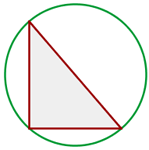
2 La hipotenusa concide con el diámetro del círculo. Empleando el teorema de Pitágoras, calculamos el radio
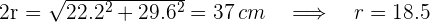
3Calculamos el área del círculo

17Calcular el lado de un triángulo equilátero inscrito en una circunferencia de 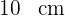 de radio.
de radio.
1Representamos gráficamente el problema
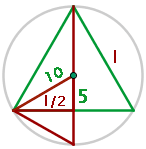
2Consideramos el triángulo rectángulo de lado  , hipotenusa
, hipotenusa  y lado restante
y lado restante  . Aplicando el teorema de Pitágoras se obtiene
. Aplicando el teorema de Pitágoras se obtiene
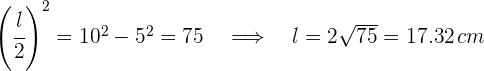
18Sobre un círculo de  de radio se traza un ángulo central de
de radio se traza un ángulo central de  . Hallar el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente.
. Hallar el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente.
1Representamos gráficamente el problema

2El área del sector es

3Para encontrar la altura del triángulo, aplicamos el teorema de Pitágoras

4Calculamos el área del triángulo equilátero
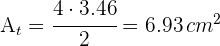
5El área del segmento circular es
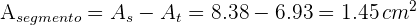
19Dado un triángulo equilátero de  de lado, hallar el área de uno de los sectores determinado por la circunferencia circunscrita y por los radios que pasan por los vértices.
de lado, hallar el área de uno de los sectores determinado por la circunferencia circunscrita y por los radios que pasan por los vértices.
1Representamos gráficamente el problema

2El centro de la circunferencia es el baricentro, por tanto 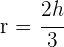
3Para encontrar la altura del triángulo, aplicamos el teorema de Pitágoras

4Calculamos el radio
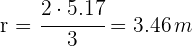
5El área de uno de los sectores determinado por la circunferencia circunscrita y por los radios que pasan por los vértices es

20Calcular el área de la corona circular determinada por las circunferencias inscrita y circunscrita a un cuadrado de  de diagonal.
de diagonal.
1Representamos gráficamente el problema

2Necesitamos conocer los radios de los círculos; para esto observamos que el diámetro de la circunferencia circunscrita es igual a la diagonal del cuadrado

3El díámetro de la circunferencia inscrita es igual al lado del cuadrado, aplicando e teorema de Pitágoras obtenemos

4El área de la corona circular es




Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Será que me pueden ayudar en este problema de encontrar el cateto ” a” en un triángulo rectángulo donde la hipotenusa mide 4 cm y el cateto “B” mide 3 cm , ayudaaaa
gracias por su tarea
GRACIAS POR SEMEJANTE TRABAJO, CREATIVO Y MUY BIEN ESTRUCTURADOS LOS PROBLEMAS
Quisiera si me pueden ayudar a resolver estos problemas : Hallar el area de la interseccion de los circulos . x2 +y2 = 9 y x2 +y2 =6x y otro es; Hallar la ongitud del arco de la curva a) x = 1/2 y elevado la 2 – i/4 desde y=1 hasta y = e b) (y +1)elevado a la 2 = 4x elevado a la 3 desde (0,,0) hasta (1.5)
longitud y perímetro con los datos r=14.5cm \theta =(3)/(4\pi )
los puntos A, B, C, D, E y F de la circunferencia de centro O y
4cm de radio determinan seis arcos congruentes. Hola profesor, ¿usted me puede ayudar con ese problemas?
El perímetro o longitud de un CD (disco compacto de forma circular) es 42𝜋
2 +8𝜋 − 4 𝑐𝑚, hallar el polinomio
que representa el valor del radio (segmento de recta que va del centro de la circunferencia a cada uno de los
puntos de esta). Teniendo en cuenta que la longitud de la circunferencia (C)= 2π r, por lo tanto se debe despejar
el radio (r).
CUAL ES EL AREA Y EL PERIMETRO DE LA CIRCUNFERENCIA QUE SE ENCUENTRA DENTRO DE UN CUADRADO DE 10 CM DE LADO
el %de 50 de $
Un parque tiene la forma que aparece en la siguiente gráfica.
En el centro hay un lago circular de 18 m de diámetro y en cada uno de los círculos pequeños de 40 dm de radio hay un árbol. El resto del parque corresponde a la zona verde que pueden disfrutar los visitantes. ¿Qué área del parque es zona verde?