Elige la opción correcta:
1De un triángulo cualquiera sabemos que tiene un ángulo de 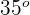 y otro de
y otro de 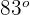 , entonces el tercer ángulo mide...
, entonces el tercer ángulo mide...
Recordemos que la suma de los  ángulos de un triángulo es
ángulos de un triángulo es  . Entonces,
. Entonces,
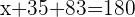
Despejamos 

Por tanto, el ángulo que falta mide 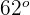
2El triángulo del ejercicio anterior es...
Para clasificar los triángulos según sus ángulos recordemos que
- Triángulo acutángulo: Si todos sus ángulos son menores a

- Triángulo rectángulo: Si tiene un ángulo de

- Triángulo obtusángulo: Si tiene un ángulo mayor a

En el ejercicio anterior, el triángulo tiene ángulos de medidas: 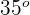 ,
, 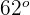 y
y 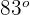 .
.
Notamos que todos son inferiores a  , por lo que se trata de un triángulo acutángulo
, por lo que se trata de un triángulo acutángulo
3Un triángulo isósceles cuyos ángulos iguales miden  cada uno es un triángulo...
cada uno es un triángulo...
Recordemos que la suma de los ángulos de un triángulo es  , por lo que, si dos ángulos miden
, por lo que, si dos ángulos miden  , el tercer ángulo mide
, el tercer ángulo mide
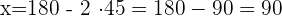
Entonces, el ángulo que falta mide 
Por tanto, se trata de un triángulo rectángulo.
4La suma de dos lados de un triángulo son  cm, entonces el otro lado puede medir...
cm, entonces el otro lado puede medir...
Como cualquier lado de un triángulo siempre es menor que la suma de los otros dos, la única opción válida es la de  cm, pues es la única cantidad menor que
cm, pues es la única cantidad menor que  cm.
cm.
5Sabemos que la medida de dos lados de un triángulo son  cm y
cm y  cm. Entonces, el tercer lado podrá medir...
cm. Entonces, el tercer lado podrá medir...
Como cualquier lado de un triángulo siempre es menor que la suma de los otros dos, en este caso

el lado que falta deberá medir menos de  cm.
cm.
Y como cualquier lado de un triángulo siempre es mayor que la diferencia de los otros dos, en este caso
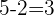
el lado que falta deberá medir más de  cm.
cm.
Por tanto, el tercer lado podrá medir más de  cm y menos de
cm y menos de  cm.
cm.
6La medida del ángulo exterior marcado en este dibujo es...

El valor de un ángulo exterior es igual a  más la suma de los dos ángulos interiores no adyacentes.
más la suma de los dos ángulos interiores no adyacentes.
Por tanto, la medida del ángulo que falta viene dada por
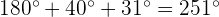
7La medida del ángulo interior del triángulo anterior que falta es...
Sabemos que la suma de los  ángulos interiores de un triángulo es
ángulos interiores de un triángulo es  . Por tanto, si llamamos
. Por tanto, si llamamos  a la medida del ángulo que falta se tendría:
a la medida del ángulo que falta se tendría:
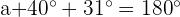
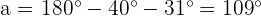
8Si tenemos un triángulo equiátero cuyo perímetro es de  cm, su lado mide...
cm, su lado mide...
Como un triángulo equilátero tiene sus tres lados iguales y su perímetro es  , tenemos que
, tenemos que

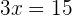
basta dividir  entre
entre  ,
,
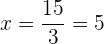
de donde, cada lado mide  cm.
cm.
9No es posible que un triángulo sea...
Un triángulo equilátero debe tener todos sus lados y ángulos iguales. Al ser obtusángulo debería tener algún ángulo mayor que  . Y por ser equilátero todos los ángulos deberían ser como este, mayor de
. Y por ser equilátero todos los ángulos deberían ser como este, mayor de  . Pero entonces la suma de los ángulos sería mayor que
. Pero entonces la suma de los ángulos sería mayor que 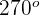 , y tendría que ser de
, y tendría que ser de  . Por tanto, es imposible que un triángulo sea obtusángulo y equilátero.
. Por tanto, es imposible que un triángulo sea obtusángulo y equilátero.
10Sabemos que uno de los ángulos agudos de un triángulo rectángulo mide 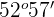 , entonces el otro ángulo agudo mide...
, entonces el otro ángulo agudo mide...
Los ángulos de un triángulo suman  . Si llamamos
. Si llamamos  el ángulo que no conocemos, entonces
el ángulo que no conocemos, entonces
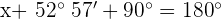
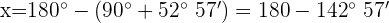
Calculamos esta diferencia

Concluimos que el otro ángulo agudo es 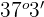
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el ejercicio 2 veo que toma como altura 10cm, cuando se supone que h que fue la medida que buscamos es la altura. Por lo tanto el área correcta es de 21.65cm2
El ejercicio 2 que me sale es el siguiente:
Un faro barre con su luz un ángulo plano de 180. Si el alcance máximo del faro es de 7 millas, ¿cuál es la longitud máxima en metros del arco correspondiente?
Que no tiene que ver con que mencionas.
Será que me pueden ayudar en este problema de encontrar el cateto ” a” en un triángulo rectángulo donde la hipotenusa mide 4 cm y el cateto “B” mide 3 cm , ayudaaaa
gracias por su tarea
GRACIAS POR SEMEJANTE TRABAJO, CREATIVO Y MUY BIEN ESTRUCTURADOS LOS PROBLEMAS
Quisiera si me pueden ayudar a resolver estos problemas : Hallar el area de la interseccion de los circulos . x2 +y2 = 9 y x2 +y2 =6x y otro es; Hallar la ongitud del arco de la curva a) x = 1/2 y elevado la 2 – i/4 desde y=1 hasta y = e b) (y +1)elevado a la 2 = 4x elevado a la 3 desde (0,,0) hasta (1.5)
longitud y perímetro con los datos r=14.5cm \theta =(3)/(4\pi )
los puntos A, B, C, D, E y F de la circunferencia de centro O y
4cm de radio determinan seis arcos congruentes. Hola profesor, ¿usted me puede ayudar con ese problemas?
El perímetro o longitud de un CD (disco compacto de forma circular) es 42𝜋
2 +8𝜋 − 4 𝑐𝑚, hallar el polinomio
que representa el valor del radio (segmento de recta que va del centro de la circunferencia a cada uno de los
puntos de esta). Teniendo en cuenta que la longitud de la circunferencia (C)= 2π r, por lo tanto se debe despejar
el radio (r).