Resuelve los siguientes problemas:
1Indica el área de un círculo de 10 cm de diámetro, redondeando a dos cifras decimales.
cm²
¿Cuál sería la longitud de la circunferencia correspondiente? Redondea también a dos cifras decimales.
cm
Como el diámetro es de 10 cm, esto implica que el radio es igual a 5 cm, pues éste siempre es la mitad del diámetro.
Reemplazando el valor del radio en la fórmula para el área tenemos que
Ahora reemplacemos el valor del radio en la fórmula para la longitud
El área del círculo es 78.54 cm² y la longitud de la circunferencia es 31.42 cm
2En una imprenta hacen pegatinas para discos de música de forma que se cubra la parte superior del CD. Sabiendo que el radio mayor mide 5.8 cm y el menor 0.7 cm aproximadamente, ¿qué área de papel utilizan para cada CD?
cm²
Sea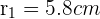 
y 
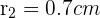los radios mayor y menor respectivamente. Para hallar el área de las pegatinas, debemos restarle el área del círculo menor al área del círculo mayor. De esta manera, nos queda la siguiente fórmula
El área de cada pegatina es 104.14 cm².
3Calcula el área de un sector circular de angulo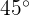 
sabiendo que la longitud de la circunferencia a la que pertenece mide 
.
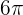cm²
Dado que la longitud mide 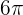, podemos utilizar la fórmula de la longitud 
para hallar el valor del radio, pues
lo cual implica que
y entonces
Después de hallar el valor del radio, estamos preparados para encontrar el área del sector circular de ángulo 
sustituyendo en su respectiva fórmula
El área del sector circular es 3.53 cm².
4Para una fiesta de cumpleaños un grupo de 6 amigos compran una tarta de 28 cm de diámetro. Si dividimos el pastel en 6 porciones iguales, ¿qué área de tarta se come cada uno?
cm²
Si el diámetro 
mide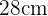 
, se sabe que el radio es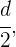 
luego el valor del radio es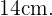 
Ya que la tarta se partirá en 
porciones, entonces el ángulo que forma cada porción es
En conclusión el área de tarta que se come cada uno es igual al área de un sector circular de radio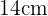 
y ángulo 
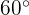. Así, el área de trozo de tarta es
Pues la fórmula para encontrar el área de un sector circular está dada por 
Cada trozo tiene como área 102.62 cm².
5Sobre un círculo de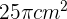 
de área trazamos un ángulo central de 
. Calcula el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente
cm²
Primero encontraremos el valor del radio. Para ello utilizaremos el valor del área del círculo y la fórmula para calcular el área. Por un lado
y también
Juntando las igualdades anteriores, obtenemos que
Ahora, calculemos el valor del área del triángulo que tiene como lados a dos radios que forman un ángulo de y la cuerda. Notemos que este triángulo es isósceles, su base mide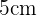 
al igual que su altura. De esta forma el área del triángulo es
El área del sector circular de ángulo y radio 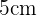, es
Para finalizar, el área que buscamos es la resta del área del anterior sector circular menos el área del triángulo. Entonces la respuesta que buscamos es
El área del segmento circular es 7.13 cm².
6Calcular el área de la zona coloreada de las siguientes figuras siendo la altura del rectángulo la mitad que la base. Redondea a dos cifras decimales.
cm²
cm
La primera figura es un hexágono con una circunferencia circunscrita, por tanto el área solicitada será el área del hexágono menos el área de la circunferencia.
Para calcular el área del hexágono debemos primero calcular su apotema 
, el cual coincide con el radio de la circunferencia. Ya que el hexágono se divide en triángulos equilateros iguales, entonces podemos formar un triángulo rectángulo circunscrito de catetos igual a 
, e hipotenusa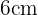 
. Para hallar el apotema utilizamos la fórmula para calcular catetos del Teorema de Pitágoras
Ahora que conocemos el valor del apotema, podemos calcular el área del hexágono a través de la fórmula del área de polígonos regulares. Dicha fórmula está dada por la siguiente expresión
donde 
representa el número de lados del polígono, que en este caso son seis, y 
es la longitud de sus lados, que sabemos es igual a seis también.
Por otro lado, como el apotema coincide con el radio del círculo, entonces
Finalmente, el área que buscamos es
La segunda figura es un rectángulo con dos circunferencias inscritas, por tanto el área pedida será el área del rectángulo menos el área de las circunferencias.
Observemos que la altura del rectángulo es igual al diámetro de la circunferencia, entonces su valor es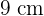 
y como el radio es la mitad de su valor, se sigue que el radio mide 
El área del rectángulo es
Luego, para el área del círculo
Por último, el área que buscamos es
El área de la primera figura es 8.65 cm² y de la segunda es 34.76cmcm²
7El radio mayor de un roscón de reyes es de 20 cm mientras que el radio menor mide 7 cm. Si cortamos un trozo con un ángulo de 20º, ¿qué área del roscón hemos cortado?.
El área que buscamos calcular es la resta del área de un sector circular de radio 
y ángulo 
menos el área de un sector circular de radio 
y ángulo . Entonces, recordando la fórmula del sector circular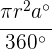 
tenemos que
El área cortada es de 61.26 cm².
8Calcular el área de la zona coloreada redondeando a dos cifras decimales
cm²
El área de la zona coloreada es el área del cuadrado menos el área del sector circular, cuyo ángulo es de 90º.
Primero calcularemos el área del sector circular cuyo ángulo es y radio igual a la longitud de un lado del cuadrado, esto es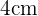 
. Luego, como la fórmula del área de un sector circular está dada por
sustituyendo los valores que hemos encontrado se tiene que
Ahora, como el área del cuadrado es el resultado de multiplicar su base por su altura, se reduce simplemente a la multiplicación de dos de sus lados. Entonces
Finalmente, el área de la zona coloreada es
El área de la zona coloreada es 3.43cm²
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores no adyacentes si el ángulo exterior mide 40 + 31 = 71 grados entonces:
La respuesta es 71 grados.
Un triángulo equilátero tienes todos sus lados iguales si el perímetro es de 15cm
Podemos calcular la longitud de cada lado
Dividiendo el perímetro entre 3
Calcule el perímetro de un triángulo isósceles de lado 13u y 5u
Una pregunta si al final de la resta de ángulos los grados son menores como lo resto si ya no hay nadie quien le preste ?
Haces la resta al revés sabiendo que el resultado va a ser negativo por ejemplo a 3 grados y 52 minutos le resto 18 grados y 22 minutos, entonces a 18 grados 22 minutos le quitas 3 grados y 52 minutos y el resultado es negativo.
: 2. Incentro en un triángulo Obtusángulo. 3. Circuncentro en un triángulo acutángulo 4. Excentro en un triángulo acutángulo.
No, no da otra opción con la que hay es suficiente.