Temas
- Elementos de la hipérbola
- Excentricidad
- Ecuación reducida de la hipérbola
- Ecuación de la hipérbola con los focos en el eje OY
- Ecuación de la hipérbola con eje paralelo a OX, y centro distinto al origen
- Ecuación de la hipérbola con eje paralelo a OY, y centro distinto al origen
- Ecuación de la hipérbola equilátera
- Ecuación de la hipérbola equilátera referida a sus asíntotas
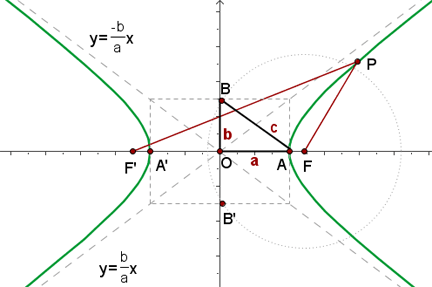
La hipérbola es el lugar geométrico de los puntos del plano cuya diferencia de distancias a los puntos fijos llamados focos es constante en valor absoluto.
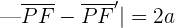 para cualquier punto
para cualquier punto  de la hipérbola.
de la hipérbola.
Elementos de la hipérbola
1Focos: Son los puntos fijos  y
y  .
.
2Eje focal, principal o real: Es la recta que pasa por los focos.
3Eje secundario o imaginario: Es la mediatriz del segmento 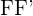 .
.
4Centro: Es el punto de intersección de los ejes.
5Vértices: Los puntos  y
y  son los puntos de intersección de la hipérbola con el eje focal.
son los puntos de intersección de la hipérbola con el eje focal.
6Radios vectores: Son los segmentos que van desde un punto de la hipérbola a los focos:  y
y  .
.
7Distancia focal: Es el segmento 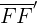 de longitud
de longitud  .
.
8Eje mayor: Es el segmento  de longitud
de longitud  .
.
9Eje menor: Es el segmento  de longitud
de longitud  .
.
Los puntos  y
y  se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio
se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio  .
.
10Ejes de simetría: Son las rectas que contienen al eje real o al eje imaginario.
11Asíntotas: Son las rectas de ecuaciones: 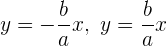
12Relación entre los semiejes: 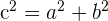
Excentricidad
La excentricidad es un parámetro que indica la abertura mayor o menor de las ramas de la hipérbola. Este número, en el caso de las hipérbolas, siempre es mayor que 1.

Ecuación reducida de la hipérbola
Se llama ecuación reducida a la ecuación de la hipérbola cuyos ejes coinciden con los ejes coordenadas, y, por tanto, el centro de hipérbola con el origen de coordenadas. Si el eje real está en el eje de abscisas las coordenadas de los focos son:
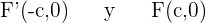
y la ecuación de la hipérbola reducida es
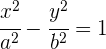
Ecuación de la hipérbola con los focos en el eje OY
Si el eje real está en el eje de abscisas las coordenadas de los focos son:

y la ecuación de la hipérbola en este caso es
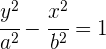
Ecuación de la hipérbola con eje paralelo a OX, y centro distinto al origen
Si el centro de la hipérbola es  y el eje principal es paralelo a OX, los focos tienen de coordenadas
y el eje principal es paralelo a OX, los focos tienen de coordenadas
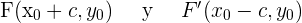
Y la ecuación de la hipérbola será:

Al quitar denominadores y desarrollar las ecuaciones se obtiene, en general, una ecuación de la forma:
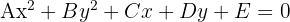
Donde  y
y  tienen signos opuestos.
tienen signos opuestos.
Ecuación de la hipérbola con eje paralelo a OY, y centro distinto al origen
Si el centro de la hipérbola  y el eje principal es paralelo a OY, los focos tienen de coordenadas
y el eje principal es paralelo a OY, los focos tienen de coordenadas
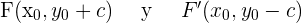
Y la ecuación de la hipérbola será:

Al quitar denominadores y desarrollar las ecuaciones se obtiene, en general, una ecuación de la forma:
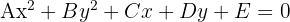
Donde  y
y  tienen signos opuestos.
tienen signos opuestos.
Ecuación de la hipérbola equilátera
Las hipérbolas en las que los semiejes son iguales se llaman equiláteras, por tanto  . Y su ecuación es:
. Y su ecuación es:
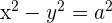
Las asíntotas tienen por ecuación:

Es decir, son las bisectrices de los cuadrantes. Además, la excentricidad es
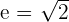
Ecuación de la hipérbola equilátera referida a sus asíntotas
Para pasar de los ejes OX, OY a los determinados por las asíntotas, bastará dar un giro de −45° alrededor del origen de coordenadas. Quedando la ecuación como:

Si efectuamos un giro de 45° en los ejes, la hipérbola que queda en el segundo y cuarto cuadrante y su ecuación será:
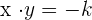













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el ejercicio número 7 hay un error. El las coordenadas de los focos aparece una “a” cuando debería ser “c”.
Una disculpa ya se corrigió.
encuentra en las coordenadas de los vértices y de los focos las longitudes de los ejes mayor y menor la distancia focal la longitud de cada uno de los lados rectos y la excentricidad de cada una de las elipses cuyas ecuaciones se dan a continuacion x^2/ 25+y^2/9=1
Halla la ecuacion de la parabola ordinaria general con elementos si su vertice está en (4,5) y su foco (7,5)
Dada la ecuación de la parábola. X2-8x-10y-4. Transformala en su forma ordinaria y comprueba su grafica con la de la figura
Determine si la gráfica de cada uno de las siguientes ecuaciones es una circunferencia,un punto o el conjunto vacío; si es la gráfica de una circunferencia dé el centro y el radio .
6×2+6y2-14x+7y-20=0
X2+y2+4x-2y+10=0
X2+y2+18x-20y+100=0
3×2+3y2-x-2y-1=
¿Cómo los puedo citar?
Puedes citar al grupo Superprof directamente 🙂
Una parábola horizontal con vértice en el origen pasa por el punto A(2,6)
Hallar la ecuación y elaborar la grafica
Qué condiciones debe cumplir “A” para que la ecuación: x2 + y2 + Ax – Ay – A2 = 0 tenga como gráfica una circunferencia? Dé las coordenadas del centro y el valor del radio.