Bienvenido al apasionante mundo de la elipse, una figura geométrica que ha cautivado a matemáticos y científicos durante siglos. En esta colección de ejercicios y problemas, explorarás los secretos y propiedades de la elipse.
La elipse es mucho más que una simple forma ovalada. Es una curva con propiedades únicas que la hacen indispensable en diversas áreas del conocimiento. A través de estos desafíos, te adentrarás en el estudio de su ecuación, sus elementos característicos como los focos y vértices, y las relaciones entre sus diferentes parámetros.
Ya seas un estudiante que recién se introduce en el mundo de la elipse o un entusiasta de las matemáticas que busca desafíos más complejos, esta colección te brindará una base sólida para comprender y aplicar los principios de la elipse en diversas situaciones. ¡Prepárate para afinar tu pensamiento analítico!

Elementos de la elipse
Representa gráficamente y determina las coordenadas de los focos, de los vértices y la excentricidad de las siguientes elipses.
1 
1 Eje mayor
La ecuación de la elipse ya está en forma canónica por lo que procedemos a obtener el valor del semieje mayor

Y así encontrar los vértices que forman el eje mayor

2 Eje menor
Entonces el valor del semieje menor es

Por lo tanto, los vértices que se encuentran en el eje menor son

3 Focos
Finalmente calculamos el valor de la distancia semifocal

Y con éste, localizar los focos

4 Excentricidad
La excentricidad es igual al cociente de la distancia semifocal y el semieje mayor

5 Gráfica
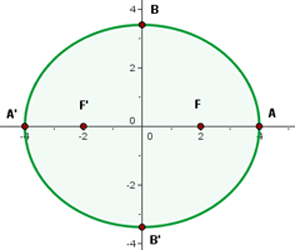
2 
1 Obtener ecuación canónica

2 Eje mayor
Obtenemos el valor del semieje mayor

Y así encontrar los vértices que forman el eje mayor

3 Eje menor
Entonces el valor del semieje menor es

Por lo tanto, los vértices que se encuentran en el eje menor son

4 Focos
Finalmente calculamos el valor de la distancia semifocal

Y con éste, localizar los focos

5 Excentricidad
La excentricidad es igual al cociente de la distancia semifocal y el semieje mayor
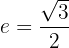
6 Gráfica

3 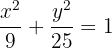
1 Eje mayor
La ecuación de la elipse ya está en forma canónica por lo que procedemos a obtener el valor del semieje mayor

Y así encontrar los vértices que forman el eje mayor

2 Eje menor
Entonces el valor del semieje menor es

Por lo tanto, los vértices que se encuentran en el eje menor son

3 Focos
Finalmente calculamos el valor de la distancia semifocal

Y con éste, localizar los focos

4 Excentricidad
La excentricidad es igual al cociente de la distancia semifocal y el semieje mayor

5 Gráfica
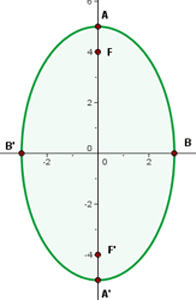
4 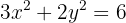
1 Obtener ecuación canónica

2 Eje mayor
La ecuación de la elipse ya está en forma canónica por lo que procedemos a obtener el valor del semieje mayor

Y así encontrar los vértices que forman el eje mayor

3 Eje menor
Entonces el valor del semieje menor es

Por lo tanto, los vértices que se encuentran en el eje menor son

4 Focos
Finalmente calculamos el valor de la distancia semifocal

Y con éste, localizar los focos

5 Excentricidad
La excentricidad es igual al cociente de la distancia semifocal y el semieje mayor

6 Gráfica
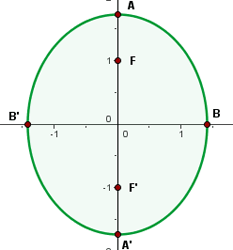
5 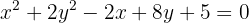
1 Obtener ecuación canónica
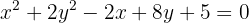
Completamos el trinomio al cuadrado perfecto
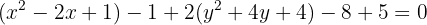
Cambiamos los trinomios por los binomios al cuadrado
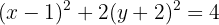
Dividimos todo por 4
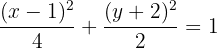
2 Centro
A partir de la ecuación de la elipse canónica encontramos el centro
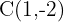
3 Eje mayor
La ecuación de la elipse ya está en forma canónica por lo que procedemos a obtener el valor del semieje mayor

Y así encontrar los vértices que forman el eje mayor

4 Eje menor
El valor del semieje menor es

Por lo tanto, los vértices que se encuentran en el eje menor son

5 Focos
Finalmente calculamos el valor de la distancia semifocal

Y con éste, localizar los focos

6 Gráfica
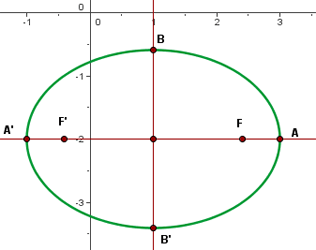
6 
1 Obtener ecuación canónica

Completamos el trinomio al cuadrado perfecto
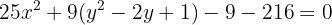
Cambiamos los trinomios por los binomios al cuadrado
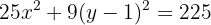
Dividimos todo por 225
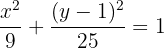
2 Centro
A partir de la ecuación de la elipse canónica encontramos el centro
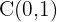
3 Eje mayor
La ecuación de la elipse ya está en forma canónica por lo que procedemos a obtener el valor del semieje mayor

Y así encontrar los vértices que forman el eje mayor

4 Eje menor
El valor del semieje menor es

Por lo tanto, los vértices que se encuentran en el eje menor son

5 Focos
Finalmente calculamos el valor de la distancia semifocal

Y con éste, localizar los focos

6 Gráfica

7 
1 Obtener ecuación canónica

Completamos el trinomio al cuadrado perfecto
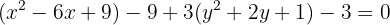
Cambiamos los trinomios por los binomios al cuadrado
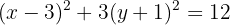
Dividimos todo por 12
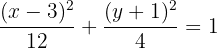
2 Centro
A partir de la ecuación de la elipse canónica encontramos el centro
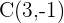
3 Eje mayor
La ecuación de la elipse ya está en forma canónica por lo que procedemos a obtener el valor del semieje mayor

Y así encontrar los vértices que forman el eje mayor

4 Eje menor
El valor del semieje menor es

Por lo tanto, los vértices que se encuentran en el eje menor son

5 Focos
Finalmente calculamos el valor de la distancia semifocal

Y con éste, localizar los focos

6 Gráfica
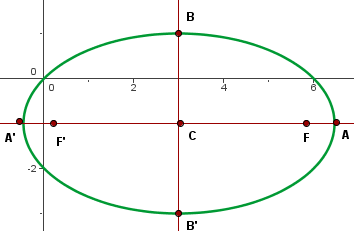
8 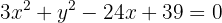
1 Obtener ecuación canónica
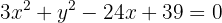
Completamos el trinomio al cuadrado perfecto

Cambiamos los trinomios por los binomios al cuadrado
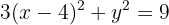
Dividimos todo por 9
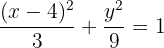
2 Centro
A partir de la ecuación de la elipse canónica encontramos el centro

3 Eje mayor
La ecuación de la elipse ya está en forma canónica por lo que procedemos a obtener el valor del semieje mayor

Y así encontrar los vértices que forman el eje mayor

4 Eje menor
El valor del semieje menor es

Por lo tanto, los vértices que se encuentran en el eje menor son

5 Focos
Finalmente calculamos el valor de la distancia semifocal

Y con éste, localizar los focos

6 Gráfica

 
Ecuación de la elipse
9 Halla la ecuación de la elipse conociendo:
1 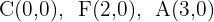
El valor de  es la distancia del centro al vértice A, mientras que el valor de
es la distancia del centro al vértice A, mientras que el valor de  es la distancia del centro al foco, entonces
es la distancia del centro al foco, entonces

Los valores  ,
,  y
y  guardan una relación pitagórica, es decir
guardan una relación pitagórica, es decir
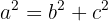
Despejamos para calcular el valor de 


Concluímos que
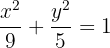
2 
El valor de  es la distancia del centro al vértice A, mientras que el valor de
es la distancia del centro al vértice A, mientras que el valor de  es la distancia del centro al foco, entonces
es la distancia del centro al foco, entonces

Los valores  ,
,  y
y  guardan una relación pitagórica, es decir
guardan una relación pitagórica, es decir
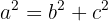
Despejamos para calcular el valor de 

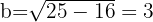
Concluímos que
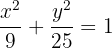
3 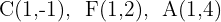
El valor de  es la distancia del centro al vértice A, mientras que el valor de
es la distancia del centro al vértice A, mientras que el valor de  es la distancia del centro al foco, entonces
es la distancia del centro al foco, entonces

Los valores  ,
,  y
y  guardan una relación pitagórica, es decir
guardan una relación pitagórica, es decir
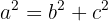
Despejamos para calcular el valor de 

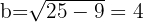
Concluímos que
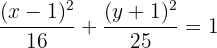
4 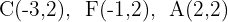
El valor de  es la distancia del centro al vértice A, mientras que el valor de
es la distancia del centro al vértice A, mientras que el valor de  es la distancia del centro al foco, entonces
es la distancia del centro al foco, entonces

Los valores  ,
,  y
y  guardan una relación pitagórica, es decir
guardan una relación pitagórica, es decir
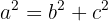
Despejamos para calcular el valor de 

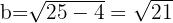
Concluímos que
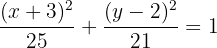
10 Escribe la ecuación canónica de la elipse con centro en el origen que pasa por el
punto 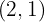 y cuyo eje menor mide
y cuyo eje menor mide  y se encuentra sobre el eje
y se encuentra sobre el eje  .
.
El eje menor mide 

Tiene centro en el origen y el eje menor está sobre el eje Y, por lo que la ecuación canónica es del tipo
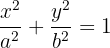
Como el punto (2,1) pertence a la elipse, sus coordenadas cumplen con la ecuación canónica

Despejamos para obtener el valor de 

Conociendo los valores de  y
y  , concluimos que
, concluimos que
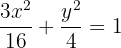
11 La distancia focal de una elipse con centro en el origen es  . Un punto de la elipse dista de sus focos
. Un punto de la elipse dista de sus focos  y
y  , respectivamente. Calcular la ecuación canónica de dicha elipse si el eje mayor está sobre el eje
, respectivamente. Calcular la ecuación canónica de dicha elipse si el eje mayor está sobre el eje  .
.
La distancia focal es igual al valor de 

Recordemos que la suma de las distancia de un punto en la elipse a los focos es igual a 

Los valores  ,
,  y
y  guardan una relación pitagórica, es decir
guardan una relación pitagórica, es decir
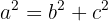
Despejamos para calcular el valor de 

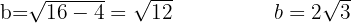
Conociendo los valores de  y
y  , concluimos que
, concluimos que

12 Escribe la ecuación canónica de la elipse que pasa por los puntos:

Como pasa por los puntos:  , entonces sus coordenadas cumplen la ecuación canónica de la elipse. Esto es
, entonces sus coordenadas cumplen la ecuación canónica de la elipse. Esto es

Resolvemos el sistema

Entonces
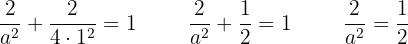
Despejamos 

Finalmente
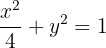
13 Determina la ecuación canónica de un elipse con centro en el origen y eje mayor en el eje  , cuya distancia focal es
, cuya distancia focal es  y el área del rectángulo con lados que midan lo mismo que los ejes (mayor y menor) es
y el área del rectángulo con lados que midan lo mismo que los ejes (mayor y menor) es 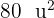 .
.
Como los lados del rectángulo son los ejes, y estos miden  y
y  entonces
entonces
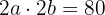
La distancia focal es igual a 

Los valores  ,
,  y
y  guardan una relación pitagórica, es decir
guardan una relación pitagórica, es decir

Esto nos conduce a tener un sistema de dos ecuaciones

De la primera ecuación despejamos  y de la segunda
y de la segunda 

Usamos  de la segunda ecuación para sustituir en la primera
de la segunda ecuación para sustituir en la primera
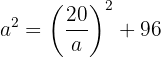
Desarrollamos
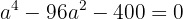
Resolvemos con la fórmula general y obtenemos el valor de 

Conociendo los valores de  y
y  , concluimos que
, concluimos que

Coordenadas de cuerdas de la elipse
14 Hallar las coordenadas de la cuerda que intercepta
la recta:  en la elipse de ecuación:
en la elipse de ecuación: 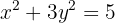 .
.
1 Encontrar puntos de intersección
Los puntos de intersección son los que resuelven el sistema de las ecuaciones de la recta y la elipse.

Para resolver podemos despejar  de la primera ecuación y elevar al cuadrado. También despejamos
de la primera ecuación y elevar al cuadrado. También despejamos 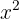 de la segunda ecuación
de la segunda ecuación

Igualamos ambas ecuaciones
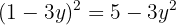
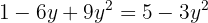
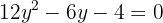
Usamos la fórmula general para encontrar las soluciones
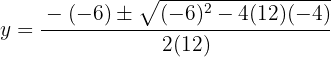
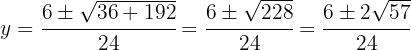
Las soluciones para la coordenada  son
son

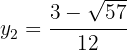
Las coordenadas  se calculan usando alguna ecuación del sistema, en este caso usaremos
se calculan usando alguna ecuación del sistema, en este caso usaremos
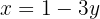
Así que los puntos de interección están dados por
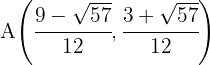

15 Hallar las coordenadas del punto medio de la cuerda que intercepta
la recta: 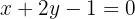 en la elipse de ecuación:
en la elipse de ecuación: 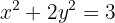 .
.
1 Encontrar puntos de intersección
Los puntos de intersección son los que resuelven el sistema de las ecuaciones de la recta y la elipse.

Para resolver podemos despejar  de la primera ecuación y elevar al cuadrado. También despejamos
de la primera ecuación y elevar al cuadrado. También despejamos 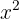 de la segunda ecuación
de la segunda ecuación

Igualamos ambas ecuaciones
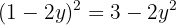
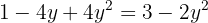

Usamos la fórmula general para encontrar las soluciones
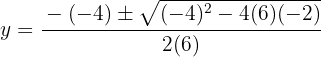
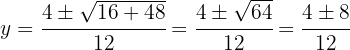
Las soluciones para la coordenada  son
son
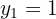
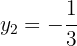
Las coordenadas  se calculan usando alguna ecuación del sistema, en este caso usaremos
se calculan usando alguna ecuación del sistema, en este caso usaremos
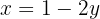
Así que los puntos de interección están dados por
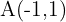
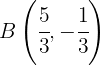
2 Encontrar punto medio
El punto medio entre los puntos A y B está dado por

¿Sigues teniendo dudas sobre cómo se resuelven las elipses? Contacta con uno de nuestros profesores para clases particulares matematicas.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el ejercicio número 7 hay un error. El las coordenadas de los focos aparece una “a” cuando debería ser “c”.
Una disculpa ya se corrigió.
encuentra en las coordenadas de los vértices y de los focos las longitudes de los ejes mayor y menor la distancia focal la longitud de cada uno de los lados rectos y la excentricidad de cada una de las elipses cuyas ecuaciones se dan a continuacion x^2/ 25+y^2/9=1
Halla la ecuacion de la parabola ordinaria general con elementos si su vertice está en (4,5) y su foco (7,5)
Dada la ecuación de la parábola. X2-8x-10y-4. Transformala en su forma ordinaria y comprueba su grafica con la de la figura
Determine si la gráfica de cada uno de las siguientes ecuaciones es una circunferencia,un punto o el conjunto vacío; si es la gráfica de una circunferencia dé el centro y el radio .
6×2+6y2-14x+7y-20=0
X2+y2+4x-2y+10=0
X2+y2+18x-20y+100=0
3×2+3y2-x-2y-1=
¿Cómo los puedo citar?
Puedes citar al grupo Superprof directamente 🙂
Una parábola horizontal con vértice en el origen pasa por el punto A(2,6)
Hallar la ecuación y elaborar la grafica
Qué condiciones debe cumplir “A” para que la ecuación: x2 + y2 + Ax – Ay – A2 = 0 tenga como gráfica una circunferencia? Dé las coordenadas del centro y el valor del radio.