
La circunferencia y su ecuación
La circunferencia se define como el lugar geométrico de los puntos del plano que equidistan de un punto fijo  que llamamos centro.
que llamamos centro.

Por lo tanto, cada punto  de la circunferencia satisface
de la circunferencia satisface

donde la distancia  se llama radio. Así, tenemos la siguiente
se llama radio. Así, tenemos la siguiente

Elevando al cuadrado la ecuación anterior, obtenemos:

La ecuación anterior se conoce como ecuación ordinaria de la circunferencia. Para obtener la ecuación general debemos desarrollar los binomios al cuadrado:

Luego reagrupamos los términos de la siguiente manera:

Consideramos los siguientes cambios:

Por tanto, la ecuación de la circunferencia se puede escribir de la siguiente manera:

la cual se conoce como la ecuación general de la circunferencia. Aquí, el centro está dado por:

y el radio satisface que:

Es importante notar que la ecuación

debe satisfacer lo siguiente para que describa una circunferencia:
1 Se cumple la siguiente desigualdad

2 No hay ningún término  (es decir,
(es decir,  y
y  no se multiplican).
no se multiplican).
3  y
y  tienen coeficiente 1.
tienen coeficiente 1.
Nota: que en caso de que  y
y  tengan coeficiente distinto a 1, entonces ambos deben tener el mismo coeficiente. De esta forma, podemos dividir la ecuación por este coeficiente para obtener la ecuación general de la circunferencia.
tengan coeficiente distinto a 1, entonces ambos deben tener el mismo coeficiente. De esta forma, podemos dividir la ecuación por este coeficiente para obtener la ecuación general de la circunferencia.
Nota: si el centro de la circunferencia coincide con el origen de las coordenadas, entonces la ecuación de la circunferencia (ya sea ordinaria o general) queda reducida a

la cual se conoce como ecuación canónica de la circunferencia.
Ejercicios de ecuación reducida de la circunferencia
1 Escribe la ecuación de la circunferencia con centro en  y radio 2.
y radio 2.
La ecuación ordinaria de la circunferencia es:

mientras que la ecuación general de la circunferencia la obtenemos al desarrollar los binomios al cuadradado:

que al agrupar las constantes, obtenemos

2 Dada la circunferencia cuya ecuación es  , encuentra su centro y radio.
, encuentra su centro y radio.
Tenemos que el centro está dado por

Por otro lado, el radio satisface:

por lo tanto, el radio es  .
.
3 Encontrar la ecuación de la circunferencia que pasa por los puntos  ,
,  y
y  .
.
Para encontrar la circunferencia que pasa por tres puntos, siempre debemos utilizar la ecuación general de la circunferencia, puesto que esto nos hará más sencillo el trabajo.
Así, sustituimos los valores de  e
e  en la ecuación:
en la ecuación:

Al sustituir  (es decir,
(es decir,  y
y  ), obtenemos
), obtenemos  , es decir,
, es decir,

Similarmente, al sustituir  obtenemos
obtenemos  ; y al sustituir
; y al sustituir  tenemos
tenemos  . Por lo tanto, tenemos el siguiente sistema de ecuaciones:
. Por lo tanto, tenemos el siguiente sistema de ecuaciones:

Resolvemos este sistema de cualquier forma que deseemos (es más sencillo si comenzamos restando la tercera ecuación de la segunda ecuación); una vez resuelto el sistema obtenemos:

De este modo, la ecuación general de la circunferencia es

4 Indicar si la ecuación  corresponde a una circunferencia. En caso afirmativo, determina el centro y el radio.
corresponde a una circunferencia. En caso afirmativo, determina el centro y el radio.
1 Notemos que los coeficientes de  and
and  son iguales (aunque no son 1); por lo tanto, dividimos toda la ecuación por 4:
son iguales (aunque no son 1); por lo tanto, dividimos toda la ecuación por 4:

2 Asimismo, notemos que no tiene ningún término  .
.
3 Por último, verifiquemos que se cumpla la desiguadad con los términos  ,
,  y
y  :
:

Por lo tanto, debido a que se cumplen las tres condiciones, entonces la ecuación sí describe a una circunferencia.
Para encontrar el centro, tenemos:

Asimismo, el radio satisface:

por lo que  .
.
5 Calcular la ecuación de la circunferencia que tiene su centro en  y es tangente al eje de las abscisas.
y es tangente al eje de las abscisas.
Se nos pide encontrar una circunferencia que es tangente a una recta. Cuando se nos pide esto, el radio siempre será la distancia que hay entre el punto y la recta (a la que deseamos que la circunferencia sea tangente). Por lo tanto, debemos encontrar la distancia entre la recta y el centro.
Primero, recordemos que el eje de abscisas es la recta  . Asimismo, la distancia entre un punto
. Asimismo, la distancia entre un punto  y una recta
y una recta  está dada por la fórmula:
está dada por la fórmula:

Por lo tanto, la distancia entre  y la recta
y la recta  es
es

Por lo tanto, la ecuación ordinaria de la circunferencia es:

La gráfica de la circunferencia se muestra en la siguiente gráfica:

6 Calcula la ecuación de la circunferencia con centro en  y que es tangente al eje de ordenadas.
y que es tangente al eje de ordenadas.
Similar al ejercicio anterior, debemos encontrar la distancia entre el punto y el eje de ordenadas. Recordemos que el eje de ordenadas está dado por la ecuación $s \equiv x = 0$. Así, la distancia es
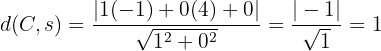
Por tanto, la ecuación de la circunferencia es

La gráfica de la circunferencia puede verse en la siguiente gráfica:

7 Calcula la ecuación de la circunferencia que tiene su centro en el punto de intersección de las rectas  $ y
$ y  , y que su radio es igual a 5.
, y que su radio es igual a 5.
Para encontrar la ecuación de la circunferencia solo debemos encontrar la intersección de las dos rectas (el radio ya lo tenemos). Para hacerlo, igualamos las ecuaciones:

de donde se sigue que  ; es decir,
; es decir,  . Sustituyendo en cualquier ecuación, obtenemos
. Sustituyendo en cualquier ecuación, obtenemos  . Por lo tanto, el centro es
. Por lo tanto, el centro es  y la ecuación de la circunferencia es
y la ecuación de la circunferencia es

o, en su forma general,

La gráfica se muestra en la siguiente figura:

8 Hallar la ecuación de la circunferencia que pasa por el punto  y que es concéntrica a la circunferencia
y que es concéntrica a la circunferencia 
Este problema puede resolver de dos maneras distintas:
La más sencilla es darnos cuenta que todas las circunferencias concéntricas a  tendrán una ecuación de la forma:
tendrán una ecuación de la forma:

Por lo tanto, debemos sustituir el punto  para poder encontrar el valor de
para poder encontrar el valor de  , lo cual nos da
, lo cual nos da

es decir,  . Por lo tanto,
. Por lo tanto,  . De esta forma, la ecuación de la circunferencia sería
. De esta forma, la ecuación de la circunferencia sería

Nota: La otra manera es determinar el centro de  y utilizar la ecuación ordinaria para poder determinar el radio.
y utilizar la ecuación ordinaria para poder determinar el radio.
La gráfica de la circunferencia se muestra en la siguiente figura:

¿Conoces nuestras clases particulares matematicas Valencia?
9 Los extremos del diámetro de una circunferencia son los puntos  y
y  . ¿Cuál es la ecuación de esta circunferencia?
. ¿Cuál es la ecuación de esta circunferencia?
Para resolver este problema debemos encontrar el radio y el centro.
El radio es la mitad del diámetro, por lo tanto, será la mitad de la distancia entre  y
y  :
:

Por otro lado, el centro es el punto medio entre  y
y  :
:

De este modo, la ecuación ordinaria de la circunferencia es:
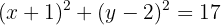
mientras que la ecuación general es:

La gráfica se muestra a continuación:

10 Hallar la ecuación de la circunferencia concéntrica a la circunferencia  y que sea tangente a la recta
y que sea tangente a la recta  .
.
Para resolver esta ecuación necesitamos encontrar el centro de la circunferencia. Por lo tanto, trabajaremos con la forma ordinaria. El centro está dado por:

una vez que encontramos el centro, debemos encontrar la distancia entre el centro y la recta dada; esta distancia será el radio:

Por lo tanto, la ecuación de la circunferencia es:

La gráfica se puede observar en la siguiente figura:

11 Hallar la ecuación de la circunferencia que pasa por los puntos  y
y  , y que tiene su centro sobre la recta
, y que tiene su centro sobre la recta  .
.
Como necesitamos utilizar el centro, entonces debemos utilizar la ecuación ordinaria (y no la general) de la circunferencia. Sea  el centro de la circunferencia y
el centro de la circunferencia y  su radio, entonces sabemos que el centro satisface
su radio, entonces sabemos que el centro satisface

Por otro lado, la ecuación de la circunferencia es

si sustituimos el punto  , tenemos
, tenemos

similarmente, si sustituimos  , entonces tenemos:
, entonces tenemos:
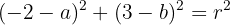
De esta forma, tenemos el siguiente sistema de ecuaciones (no lineal):

Para resolverlo, igualaremos las primeras dos ecuaciones (ya que ambas son igual a  ):
):

Si desarrollamos los binomios y cancelamos términos apropiados, obtenemos:

Luego, de la tercera ecuación despejamos  para obtener
para obtener  . Al sustituirlo en la ecuación anterior nos da
. Al sustituirlo en la ecuación anterior nos da

De aquí se sigue que 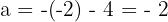 . Por último, sustituyendo
. Por último, sustituyendo  y
y  en la primera ecuación del sistema de ecuaciones obtenemos
en la primera ecuación del sistema de ecuaciones obtenemos  . Por lo tanto, la ecuación ordinaria de la circunferencia es
. Por lo tanto, la ecuación ordinaria de la circunferencia es

La gráfica se aprecia en la siguiente figura:

12 Calcula la ecuación de la circunferencia que pasa por el punto  , cuyo radio
, cuyo radio  y cuyo centro se halla en la bisectriz del primer y tercer cuadrantes.
y cuyo centro se halla en la bisectriz del primer y tercer cuadrantes.
Primero debemos notar que la bisectriz del primer y tercer cuadrantes es la recta  o
o  . Esto es, el centro
. Esto es, el centro  debe cumplir que
debe cumplir que  por lo tanto, escribimos el centro de la forma
por lo tanto, escribimos el centro de la forma  .
.
Sabemos que pasa por el punto  y que el radio es
y que el radio es  , sustituyendo en la forma ordinaria de la circunferencia obtenemos
, sustituyendo en la forma ordinaria de la circunferencia obtenemos

Sólo tenemos a  como incógnita, por lo que esa ecuación es sucificente. Desarrollamos los binomios:
como incógnita, por lo que esa ecuación es sucificente. Desarrollamos los binomios:

Por lo que tenemos una ecuación cuadrática. Utilizando la fórmula general (o cualquier otro método), llegamos a que 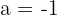 y
y  .
.
Por lo tanto, hay dos circunferencias que cumplen con las condiciones del problema. La primera tiene el centro en  , por lo que su ecuación es (primero en forma ordinaria y luego en forma general):
, por lo que su ecuación es (primero en forma ordinaria y luego en forma general):

y la segunda circunferencia tiene el centro en  , por lo que su ecuación es:
, por lo que su ecuación es:

La gráfica de la primera circunferencia se muestra a continuación:

Encuentra a tu profesor de matematicas online en Superprof.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el ejercicio número 7 hay un error. El las coordenadas de los focos aparece una “a” cuando debería ser “c”.
Una disculpa ya se corrigió.
encuentra en las coordenadas de los vértices y de los focos las longitudes de los ejes mayor y menor la distancia focal la longitud de cada uno de los lados rectos y la excentricidad de cada una de las elipses cuyas ecuaciones se dan a continuacion x^2/ 25+y^2/9=1
Halla la ecuacion de la parabola ordinaria general con elementos si su vertice está en (4,5) y su foco (7,5)
Dada la ecuación de la parábola. X2-8x-10y-4. Transformala en su forma ordinaria y comprueba su grafica con la de la figura
Determine si la gráfica de cada uno de las siguientes ecuaciones es una circunferencia,un punto o el conjunto vacío; si es la gráfica de una circunferencia dé el centro y el radio .
6×2+6y2-14x+7y-20=0
X2+y2+4x-2y+10=0
X2+y2+18x-20y+100=0
3×2+3y2-x-2y-1=
¿Cómo los puedo citar?
Puedes citar al grupo Superprof directamente 🙂
Una parábola horizontal con vértice en el origen pasa por el punto A(2,6)
Hallar la ecuación y elaborar la grafica
Qué condiciones debe cumplir “A” para que la ecuación: x2 + y2 + Ax – Ay – A2 = 0 tenga como gráfica una circunferencia? Dé las coordenadas del centro y el valor del radio.