El teorema de Rolle obtiene su nombre de Michel Rolle (1652 - 1719), un matemático francés. Rolle fue uno de los primeros matemáticos en trabajar en el desarrollo del cálculo, a pesar de que fue uno de los críticos de las bases de esta área. Asimismo, es uno de los inventores del procedimiento conocido como eliminación gausiana.

Enunciado del teorema
El teorema de Rolle nos permite afirmar si una función  tiene un punto crítico en un intervalo dado. Este teorema se enuncia como sigue:
tiene un punto crítico en un intervalo dado. Este teorema se enuncia como sigue:
Teorema: Sea  una función que
una función que
1 es continua en  ,
,
2 es derivable en  ,
,
3 y cumple que  .
.
Entonces existe algún punto 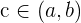 tal que
tal que 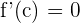 .
.
Gráficamente el teorema se interpreta como que existe un punto 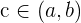 en el que la recta tangente es parallela al eje-x (siempre que se cumplan las hipótesis del teorema). Justo como se observa la siguiente figura:
en el que la recta tangente es parallela al eje-x (siempre que se cumplan las hipótesis del teorema). Justo como se observa la siguiente figura:

Si alguna de las hipótesis falla, entonces no podemos concluir que no existe punto tal que 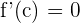 . Es decir, es posible que
. Es decir, es posible que 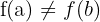 y que todavía exista un punto
y que todavía exista un punto 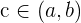 tal que
tal que  .
.
Ejemplos y ejercicios
1 Verifica si se cumplen las hipótesis del teorema de Rolle para la siguiente función
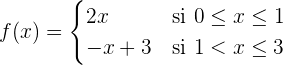
en el intervalo 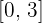 .
.
Debemos verificar las tres hipótesis del teorema de Rolle:
\begin{enumerate}
\item Primero debemos comprobar que la función sea continua. Cada "trozo" de la función ya sabemos que sí es continua porque son polinomios. Por lo tanto, sólo debemos verificar la continuidad en el punto  . Calculamos primero el límite por la izquierda:
. Calculamos primero el límite por la izquierda:

y ahora calculamos el límite por la derecha:
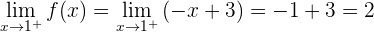
Como los límites son iguales (y la función también vale 2 cuando  ), entonces concluímos que la función es continua.
), entonces concluímos que la función es continua.
\item Ahora debemos verificar que la función sea diferenciable en todo el intervalo  . Para empezar, la función es diferenciable en los intervalos
. Para empezar, la función es diferenciable en los intervalos  y
y  ya que en esos trozos, la función está definida por polinomios.
ya que en esos trozos, la función está definida por polinomios.
Por lo tanto, debemos comprobar que la función sea diferenciable en  , para ello, calculamos las "derivadas laterales". Primero, encontramos la derivada de la función. Para el intervalo
, para ello, calculamos las "derivadas laterales". Primero, encontramos la derivada de la función. Para el intervalo  , tenemos:
, tenemos:

mientras que para  , la derivada es
, la derivada es
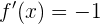
De aquí se sigue que  . Por lo tanto, la derivada no está definida en
. Por lo tanto, la derivada no está definida en  y la función no es diferenciable en todo el intervalo.
y la función no es diferenciable en todo el intervalo.
\end{enumerate}
Por tanto, una de las hipótesis falla. Así, no podemos utilizar el teorema de Rolle para asegurar la existencia de un valor 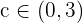 tal que
tal que 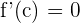 (de hecho, no existe ese valor).
(de hecho, no existe ese valor).
2 ¿Se puede utilizar el teorema de Rolle en la función 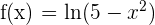 para el intervalo
para el intervalo 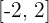 ?
?
De nuevo, verificamos las hipótesis una por una:
1 Sabemos que la función 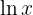 es continua para todo
es continua para todo 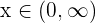 . Por lo tanto, si el argumento de la función es mayor a cero (y contínuo), entonces sabremos que
. Por lo tanto, si el argumento de la función es mayor a cero (y contínuo), entonces sabremos que  también es continua.
también es continua.
Como 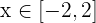 , entonces
, entonces 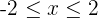 . De aquí se sigue que
. De aquí se sigue que
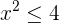
Que, al restar  a ambos lados, obtenemos
a ambos lados, obtenemos
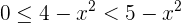
Por tanto, concluimos que  . Además,
. Además, 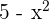 es un polinomio (es decir, continuo y derivable). Así,
es un polinomio (es decir, continuo y derivable). Así,

es también continua.
2 La comprobación de la diferenciabilidad es igual que la comprobación de la continuidad. Sabemos que 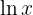 es diferenciable en
es diferenciable en 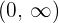 . Por lo tanto, mientras el argumento satisfaga que es mayor a 0 y sea diferenciable, entonces
. Por lo tanto, mientras el argumento satisfaga que es mayor a 0 y sea diferenciable, entonces  también lo será.
también lo será.
Como  y
y 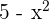 es diferenciable, entonces
es diferenciable, entonces  es diferenciable también.
es diferenciable también.
3 Por último, debemos verificar que  :
:

mientraas que
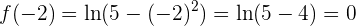
por tanto, sí se cumple que  .
.
Por tanto, concluímos que sí se cumplen todas las hipótesis del teorema de Rollo. Así, debe existir algún  tal que
tal que 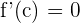 . De hecho, el valor de c es
. De hecho, el valor de c es 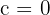 , el cual podemos obtener al calcular la derivada de
, el cual podemos obtener al calcular la derivada de  .
.
3 Utiliza el teorema de Rolla para comprobar que 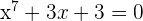 tiene una única raíz.
tiene una única raíz.
Pista: utiliza el teorema de Rolle.
El polinomio 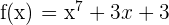 es impar, por lo tanto sabemos que debe tener al menos una raíz. Es decir, existe un valor
es impar, por lo tanto sabemos que debe tener al menos una raíz. Es decir, existe un valor  tal que
tal que 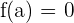 .
.
Por reducción al absudo, supongamos que el polinomio tiene dos o más raíces diferentes. Sean estas raíces 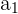 y
y  , donde
, donde  .
.
Sabemos que  es un polinomio. Por lo tanto, es continuo y diferenciable en toda
es un polinomio. Por lo tanto, es continuo y diferenciable en toda  .
.
Además, como 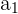 y
y  son raíces, entonces
son raíces, entonces 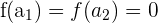 .
.
Por tanto, las hipótesis del teorema de Rolle se cumplen para el intervalo  . Así, por el teorema de Rolle, debe existir
. Así, por el teorema de Rolle, debe existir  tal que
tal que 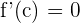 .
.
Sin embargo, la derivada de  es
es
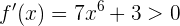
la cual siempre es mayor a 0. Es decir, no existe  tal que
tal que 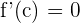 .
.
Así, tenemos una contradicción (decimos que  existe y que no existe). Como esta contradicción surge de asumir que
existe y que no existe). Como esta contradicción surge de asumir que  tiene dos o más raíces diferentes, entonces podemos concluir que
tiene dos o más raíces diferentes, entonces podemos concluir que  tiene exactamente una raíz real.
tiene exactamente una raíz real.
4 ¿La función 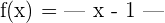 satisface las hipótesis del teorema de Rolle en el intervalo
satisface las hipótesis del teorema de Rolle en el intervalo  ?
?
Comprobamos las hipótesis una por una:
1 Sabemos que la función  (valor absoluto) es continua para todo
(valor absoluto) es continua para todo  . Por tanto,
. Por tanto,  es continua.
es continua.
2 Para comprobar que  es diferenciable, notemos que:
es diferenciable, notemos que:
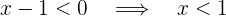
por lo tanto, la función se puede escribir como
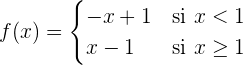
Luego calculamos las derivadas laterales en  :
:
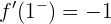
y
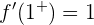
de donde se sigue que 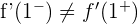 . Así,
. Así,  no es diferenciable en todo el intervalo
no es diferenciable en todo el intervalo  .
.
En consecuencia, no se cumplen las hipótesis del teorema de Rolle.
5 Verifica que la función 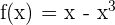 satisfaga las hipótesis del teorema de Rolle en los intervalos
satisfaga las hipótesis del teorema de Rolle en los intervalos  y
y  . En caso afirmativo, encuentra los valores
. En caso afirmativo, encuentra los valores  tales que
tales que 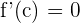 .
.
Como  es un polinomio, entonces es continua y diferenciable en todo
es un polinomio, entonces es continua y diferenciable en todo  . Por lo tanto, sólo debemos verificar que
. Por lo tanto, sólo debemos verificar que
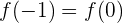
y que

Así, para  :
:
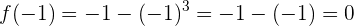
para  :
:
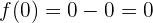
y para  :
:
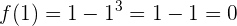
Por lo tanto, las hipótesis del teorema de Rolle se cumplen para el intervalo  y
y  .
.
Ahora encontramos los valores de  tales que
tales que 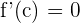 . Para hacerlo, primero encontramos la derivada de
. Para hacerlo, primero encontramos la derivada de  :
:
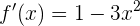
Ahora igualamos a 0:

de donde se sigue que

Así,
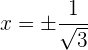
Notemos que  y que
y que 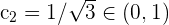 . Con lo que encontramos los valores de
. Con lo que encontramos los valores de  tales que
tales que 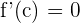 .
.
6 Verifica que la función  satisface las hipótesis del teorema de Rolle en el intervalo
satisface las hipótesis del teorema de Rolle en el intervalo  .
.
Debemos verificar las hipótesis una por una. Sin embargo, la continuidad y la diferenciabilidad son muy sencillas ya que  es un polinomio (y por tanto, diferenciable y continuo).
es un polinomio (y por tanto, diferenciable y continuo).
Así, sólo debemmos verificar que 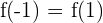 :
:

y

Por lo tanto 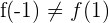 .
.
Podemos concluir, entonces, que no se cumplen las hipótesis del teorema de Rolle.
7 Demuestra que la ecuación 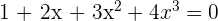 tiene una única solución.
tiene una única solución.
Pista: utiliza el teorema de Rolle.
Al igual que en algún ejercicio anterior, procedemos por reducción al absurdo.
En primer lugar, sabemos que 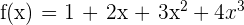 tiene al menos una raíz al ser un polinomio impar.
tiene al menos una raíz al ser un polinomio impar.
Por reducción al absurdo, suponemos que existe más de una raíz real (diferente). Es decir, existen 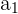 y
y  , tales que
, tales que 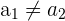 ,
,  y
y

Como  es un polinomio, entonces es continuo y diferenciable. Por lo tanto, se cumplen todas las hipótesis del teorema de Rolle en el intervalo
es un polinomio, entonces es continuo y diferenciable. Por lo tanto, se cumplen todas las hipótesis del teorema de Rolle en el intervalo  .
.
Así, debe existir  tal que
tal que 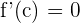 .
.
Sin embargo, la derivada de  es
es

cuyo discriminate es
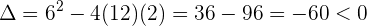
lo que significa que  no tiene raíces, es decir, no existen
no tiene raíces, es decir, no existen  tales que
tales que 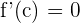 . Así, tenemos una contradicción.
. Así, tenemos una contradicción.
Por tanto, concluimos que  tiene, a lo más, una única raíz.
tiene, a lo más, una única raíz.
8 ¿Cuántas raíces tiene la ecuación 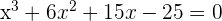 ?
?
Este ejercicio es muy similar al anterior.
En primer lugar, sabemos que 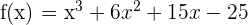 tiene al menos una raíz, debido a que es un polinomio de grado impar.
tiene al menos una raíz, debido a que es un polinomio de grado impar.
Ahora suponemos que existe más de una raíz real (diferente). Es decir, que existen 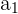 y
y  , tales que
, tales que 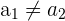 ,
,  y
y

De nuevo, como  es un polinomio, entonces es continuo y diferenciable. Por lo tanto, se cumplen todas las hipótesis del teorema de Rolle en el intervalo
es un polinomio, entonces es continuo y diferenciable. Por lo tanto, se cumplen todas las hipótesis del teorema de Rolle en el intervalo  .
.
Así, debe existir  tal que
tal que 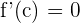 .
.
Sin embargo, la derivada de  es
es

cuyo discriminate es

lo que significa que  no tiene raíces, es decir, no existen
no tiene raíces, es decir, no existen  tales que
tales que 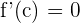 . Así, tenemos una contradicción.
. Así, tenemos una contradicción.
Por tanto, concluimos que  tiene, a lo más, una única raíz (diferente). Notemos que es todavía posible que hayan más raíces iguales (es decir, que la raíz tenga multiplicidad diferente a 1).
tiene, a lo más, una única raíz (diferente). Notemos que es todavía posible que hayan más raíces iguales (es decir, que la raíz tenga multiplicidad diferente a 1).
9 Demuestra que la ecuación 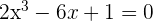 tiene una única solución real en el intervalo
tiene una única solución real en el intervalo  .
.
De nuevo, procedemos por reducción al absurdo. No obstante, el procedimiento ahora será ligeramente diferente.
En primer lugar, sabemos que  tiene al menos una raíz al ser un polinomio impar. Pero no podemos asegurar con esto que la raíz está en el intervalo
tiene al menos una raíz al ser un polinomio impar. Pero no podemos asegurar con esto que la raíz está en el intervalo  . Para ello, evaluamos la función en los extremos del intervalo:
. Para ello, evaluamos la función en los extremos del intervalo:
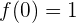
y
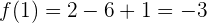
Así, 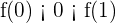 . Luego, como
. Luego, como  es continua, entonces por el teorema del valor intermedio, existe
es continua, entonces por el teorema del valor intermedio, existe 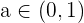 tal que
tal que 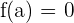 . Nota: no debemos confundir el teorema del valor intermedio con el teorema de Rolle.
. Nota: no debemos confundir el teorema del valor intermedio con el teorema de Rolle.
Por reducción al absurdo, suponemos que existe más de una raíz real (diferente) en el intervalo  . Es decir, existen
. Es decir, existen 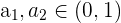 , tales que
, tales que 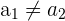 ,
,  y
y

Como  es un polinomio, entonces es continuo y diferenciable. Por lo tanto, se cumplen todas las hipótesis del teorema de Rolle en el intervalo
es un polinomio, entonces es continuo y diferenciable. Por lo tanto, se cumplen todas las hipótesis del teorema de Rolle en el intervalo  .
.
Así, debe existir 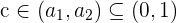 tal que
tal que 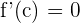 . Notemos que se debe cumplir que
. Notemos que se debe cumplir que 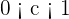 .
.
Luego, la derivada de  es
es
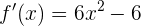
que al igualar a 0, tenemos

es decir 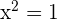 . Por tanto, las raíces son
. Por tanto, las raíces son  y
y  . Sin embargo, ninguna de esta raíces pertenece al intervalo
. Sin embargo, ninguna de esta raíces pertenece al intervalo  , lo cual contradice el teorema de Rolle.
, lo cual contradice el teorema de Rolle.
Por tanto, concluimos que  tiene una única raíz en el intervalo
tiene una única raíz en el intervalo  .
.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3
4(x+h)-4x/h =4x+4h-4x/h= 4h/h= 4