¡Bienvenido a nuestra página dedicada a ejercicios de máximos y mínimos! En este espacio, exploraremos el apasionante campo de la optimización matemática y te brindaremos los conocimientos y las estrategias necesarias para resolver problemas que involucran encontrar los valores máximos y mínimos de funciones.
Los problemas de máximos y mínimos se encuentran en diversas áreas, como la física, la economía, la ingeniería y muchas otras. Estos desafíos nos invitan a encontrar los puntos críticos de una función, donde la pendiente es cero, y determinar si esos puntos corresponden a máximos o mínimos locales.
Aquí, aprenderás a identificar las características clave de una función que te permitirán determinar sus máximos y mínimos. Haremos esto presentándote una amplia variedad de ejercicios, los cuáles resolveremos utilizando el criterio de la segunda derivada.
Nuestro objetivo es ayudarte a desarrollar tu capacidad para encontrar soluciones óptimas, fortalecer tu razonamiento analítico y promover tu confianza en las matemáticas. Disfruta y aprende con los distintos ejercicios, junto con las explicaciones claras y detalladas que hemos creado para ti. ¡Vuélvete todo un experto en calcular máximos y mínimos de funciones!
Utilizar el criterio de la segunda derivada para calcular los máximos y mínimos locales de las siguientes funciones:
1 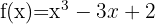
Comenzamos por encontrar la primera y la segunda derivada de la función dada:
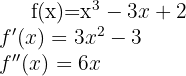
Ahora encontremos los puntos críticos  a través de la solución (o soluciones) de la ecuación
a través de la solución (o soluciones) de la ecuación  , es decir
, es decir 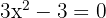 . Las soluciones de esta ecuación son
. Las soluciones de esta ecuación son 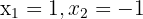 .
.
Finalmente se evalúa  en los puntos críticos
en los puntos críticos  y determinar si
y determinar si  o
o  .
.
Tenemos entonces que
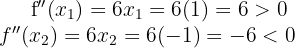
Entonces por el criterio de la segunda derivada, la función  tiene un mínimo local en
tiene un mínimo local en  y un máximo local en
y un máximo local en  . Los valores correspondientes de la función son:
. Los valores correspondientes de la función son:

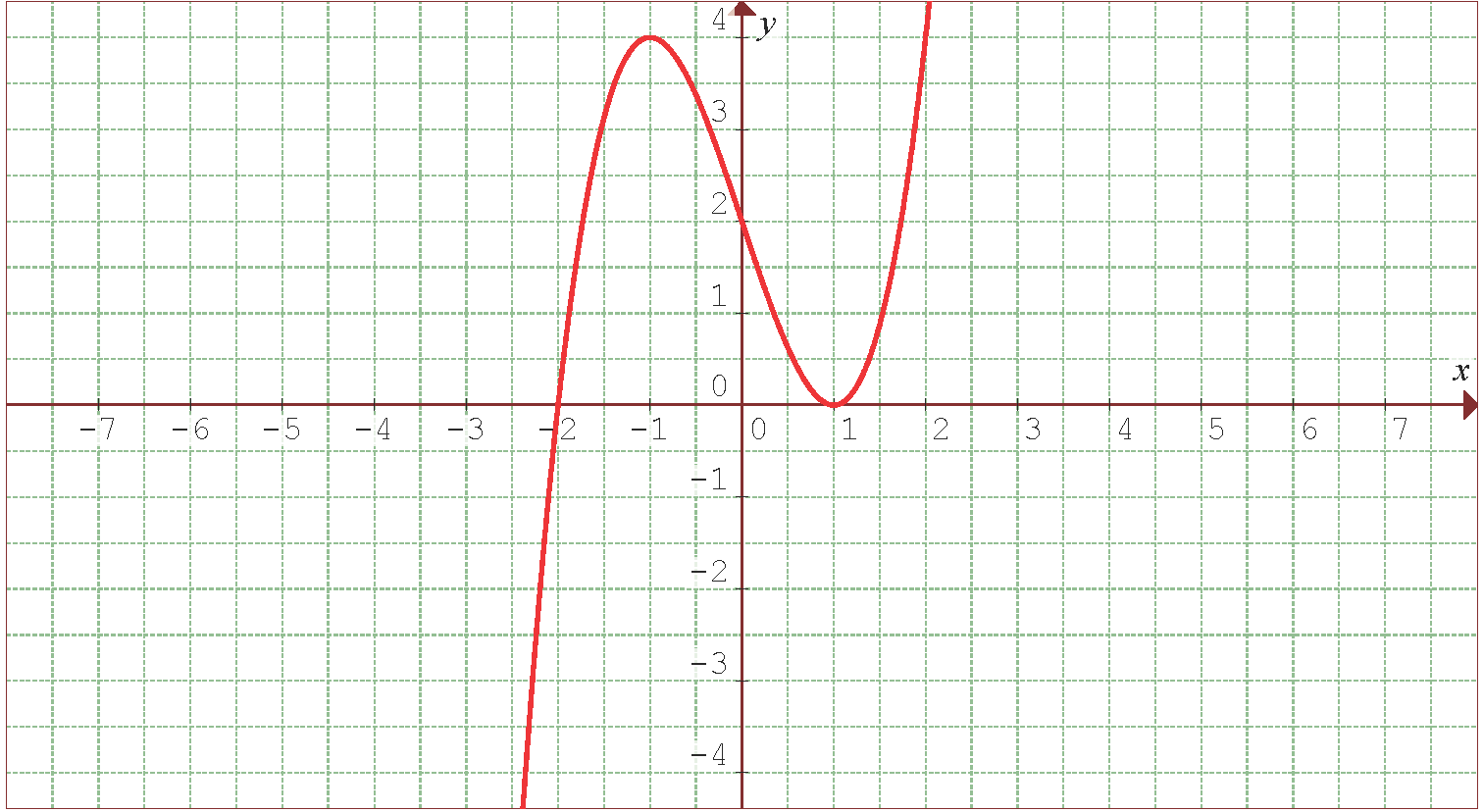
La siguiente Figura muestra la gráfica de la función  propuesta.
propuesta.
2 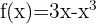
Comenzamos por encontrar la primera y la segunda derivada de la función dada:
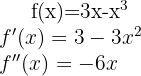
Ahora encontremos los puntos críticos  a través de la solución (o soluciones) de la ecuación
a través de la solución (o soluciones) de la ecuación  , es decir
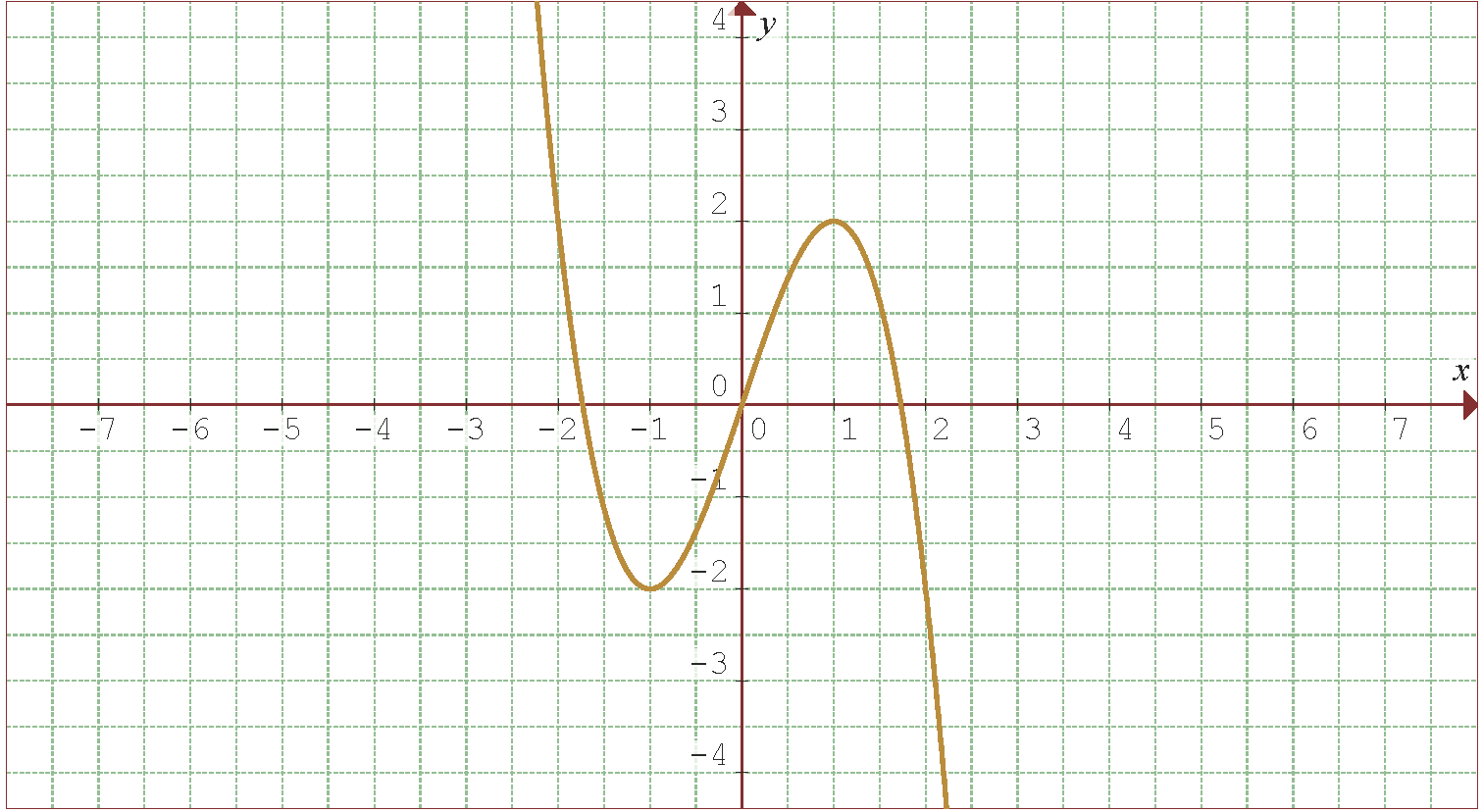
, es decir 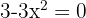 . Las soluciones de esta ecuación son
. Las soluciones de esta ecuación son  .
.
Finalmente se evalúa  en los puntos críticos
en los puntos críticos  y determinar si
y determinar si  o
o  . Tenemos entonces que
. Tenemos entonces que

Entonces por el criterio de la segunda derivada, la función  tiene un máximo local en
tiene un máximo local en  y un mínimo local en
y un mínimo local en  . Los valores correspondientes de la función son:
. Los valores correspondientes de la función son:

La siguiente Figura muestra la gráfica de la función  propuesta.
propuesta.
3 
Comenzamos por encontrar la primera y la segunda derivada de la función dada:
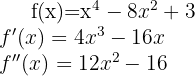
Ahora encontremos los puntos críticos  a través de la solución (o soluciones) de la ecuación
a través de la solución (o soluciones) de la ecuación  , es decir
, es decir 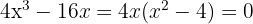 . Las soluciones de esta ecuación son
. Las soluciones de esta ecuación son  .
.
Finalmente se evalúa  en los puntos críticos
en los puntos críticos  y determinar si
y determinar si  o
o  . Tenemos entonces que
. Tenemos entonces que
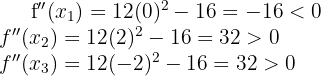
Entonces por el criterio de la segunda derivada, la función  tiene un máximo local en
tiene un máximo local en  y dos mínimos locales en
y dos mínimos locales en  y
y  . Los valores correspondientes de la función son:
. Los valores correspondientes de la función son:

La siguiente Figura muestra la gráfica de la función  propuesta.
propuesta.

4
Comenzamos por encontrar la primera y la segunda derivada de la función dada:
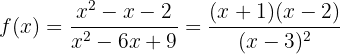
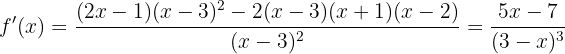
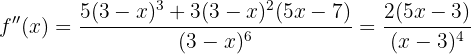
Ahora encontremos el punto crítico  a través de la solución de la ecuación
a través de la solución de la ecuación  , es decir
, es decir 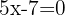 , cuya solución es
, cuya solución es 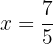 .
.
Finalmente se evalúa  en el punto crítico
en el punto crítico  y determinar si
y determinar si  o
o  . Tenemos entonces que
. Tenemos entonces que

Entonces por el criterio de la segunda derivada, la función  tiene un mínimo local en
tiene un mínimo local en 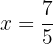 . El valor correspondiente de la función es:
. El valor correspondiente de la función es:
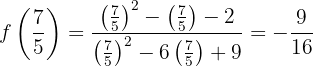
La siguiente Figura muestra la gráfica de la función  propuesta.
propuesta.

5 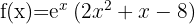
Comenzamos por encontrar la primera y la segunda derivada de la función dada:
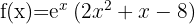
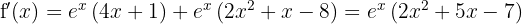

Ahora encontremos los puntos críticos  a través de la solución (o soluciones) de la ecuación
a través de la solución (o soluciones) de la ecuación  , es decir
, es decir  . Las soluciones de esta ecuación son
. Las soluciones de esta ecuación son 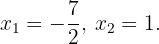 .
.
Finalmente se evalúa 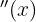 en los puntos críticos
en los puntos críticos  y determinar si
y determinar si  o
o  . Tenemos entonces que
. Tenemos entonces que
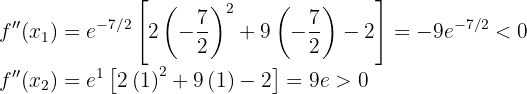
Entonces por el criterio de la segunda derivada, la función  tiene un máximo local en
tiene un máximo local en 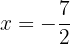 y un mínimo local en
y un mínimo local en  . Los valores correspondientes de la función son:
. Los valores correspondientes de la función son:
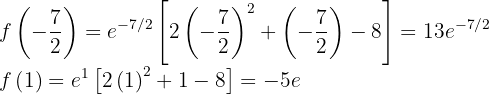
La siguiente Figura muestra la gráfica de la función  propuesta.
propuesta.
6 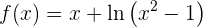
Comenzamos por encontrar la primera y la segunda derivada de la función dada:
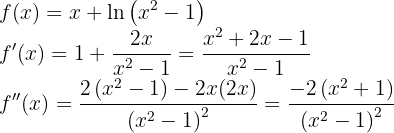
Ahora encontremos los puntos críticos  a través de la solución (o soluciones) de la ecuación
a través de la solución (o soluciones) de la ecuación 
, es decir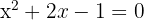 . Las soluciones de esta ecuación son
. Las soluciones de esta ecuación son 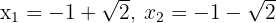 , sin embargo, dado que el dominio de la función es
, sin embargo, dado que el dominio de la función es  , es claro que
, es claro que 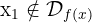
(esto debido a que 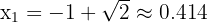 ). Por lo tanto, el único punto crítico a considerar es
). Por lo tanto, el único punto crítico a considerar es 
.
Finalmente se evalúa  en el punto crítico
en el punto crítico  y determinar si
y determinar si  o
o  . Tenemos entonces que
. Tenemos entonces que

Entonces por el criterio de la segunda derivada, la función  tiene un máximo local en
tiene un máximo local en 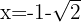 . El valor correspondiente de la función es:
. El valor correspondiente de la función es:

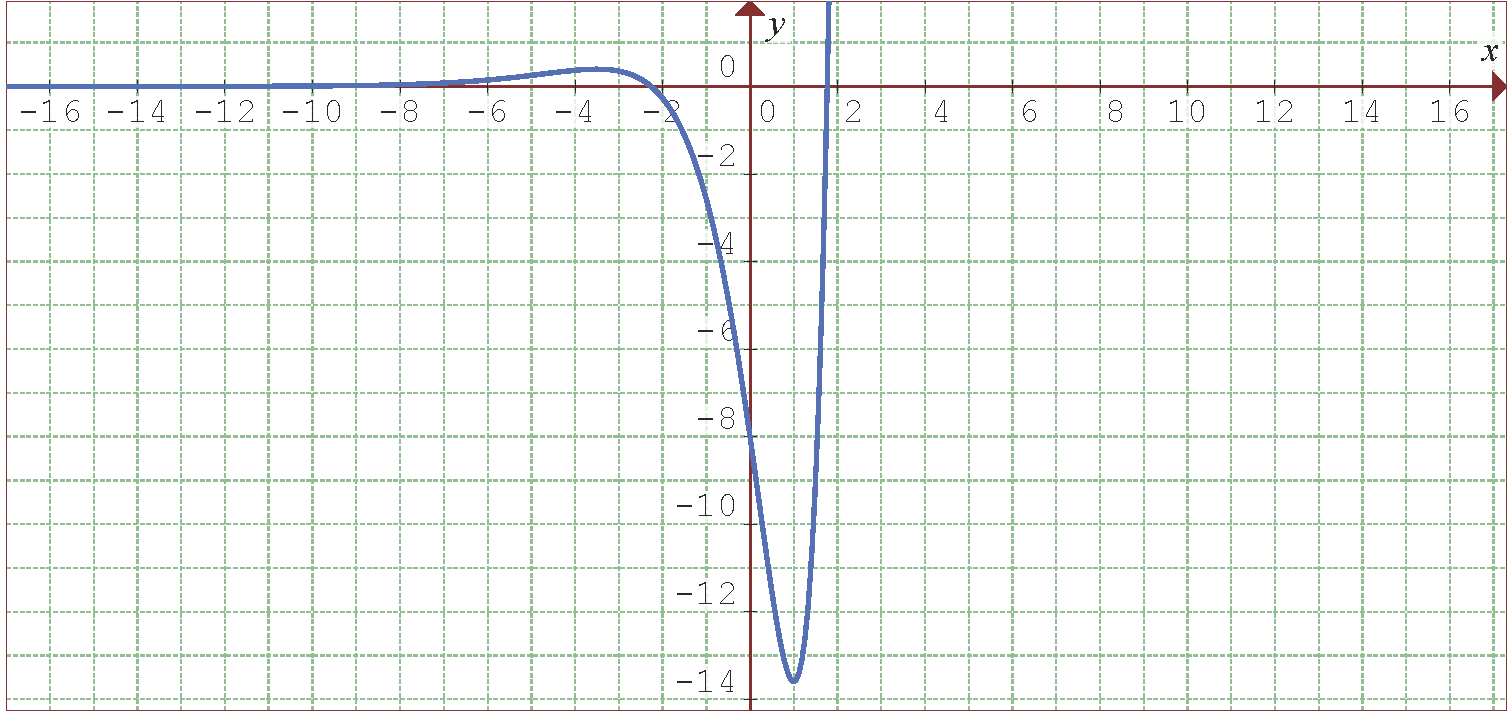
La siguiente Figura muestra la gráfica de la función  propuesta.
propuesta.
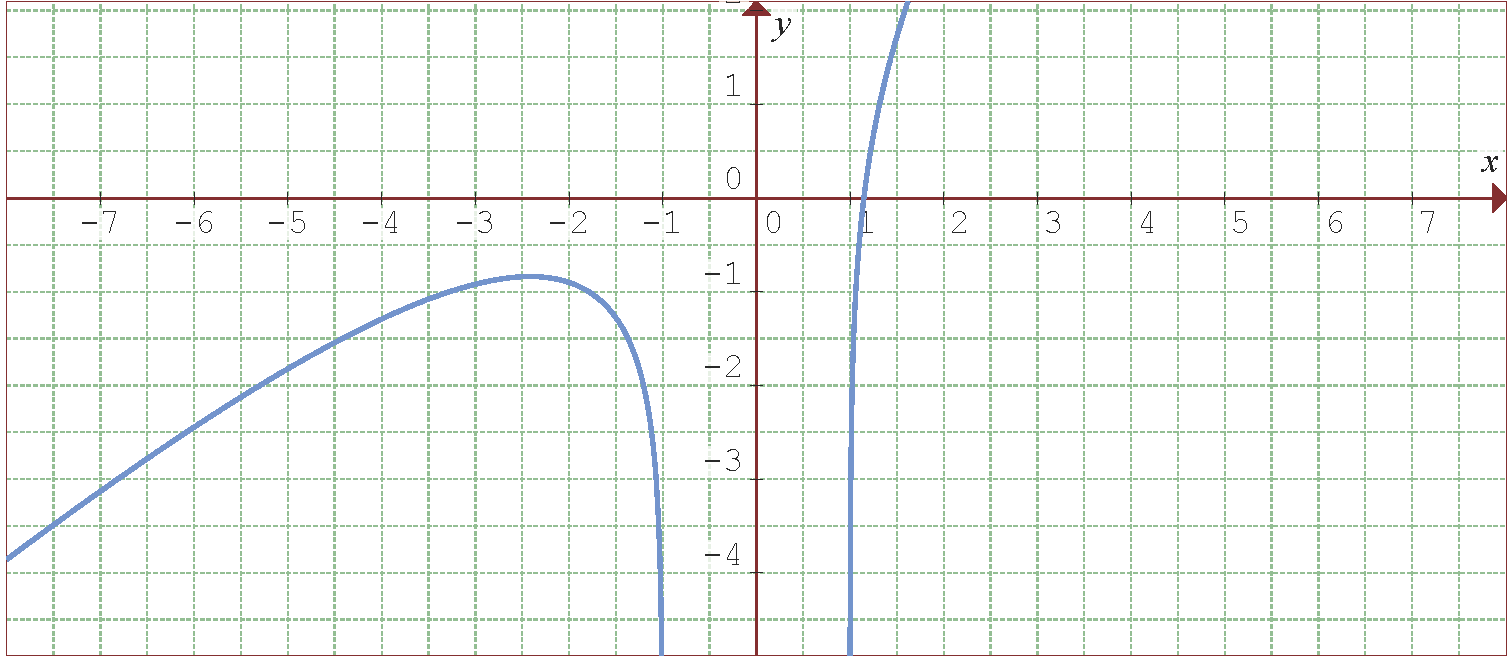
7 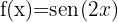
Comenzamos por encontrar la primera y la segunda derivada de la función dada:
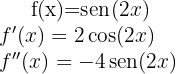
Ahora encontremos los puntos críticos  a través de la solución (o soluciones) de la ecuación
a través de la solución (o soluciones) de la ecuación 
, es decir  . Para esto, sea
. Para esto, sea  , entonces tenemos
, entonces tenemos 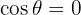 , cuyas soluciones están dadas por:
, cuyas soluciones están dadas por:
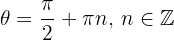
Luego, regresando a la variable original tenemos que los puntos críticos están dados por:
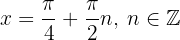
Ahora se evalúa  en los puntos críticos
en los puntos críticos  y determinar si
y determinar si  o
o  . Para esto, consideremos dos casos:
. Para esto, consideremos dos casos:
Si 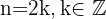 (par), entonces
(par), entonces 
, por lo que
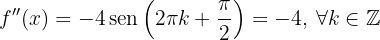
Si  (impar), entonces
(impar), entonces 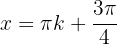
, por lo que
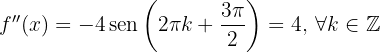
Por lo tanto, por el criterio de la segunda derivada, la función  tiene sus máximos locales en
tiene sus máximos locales en 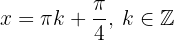 y los mínimos locales en
y los mínimos locales en 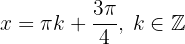 .
.
Además los valores correspondientes para la función son:

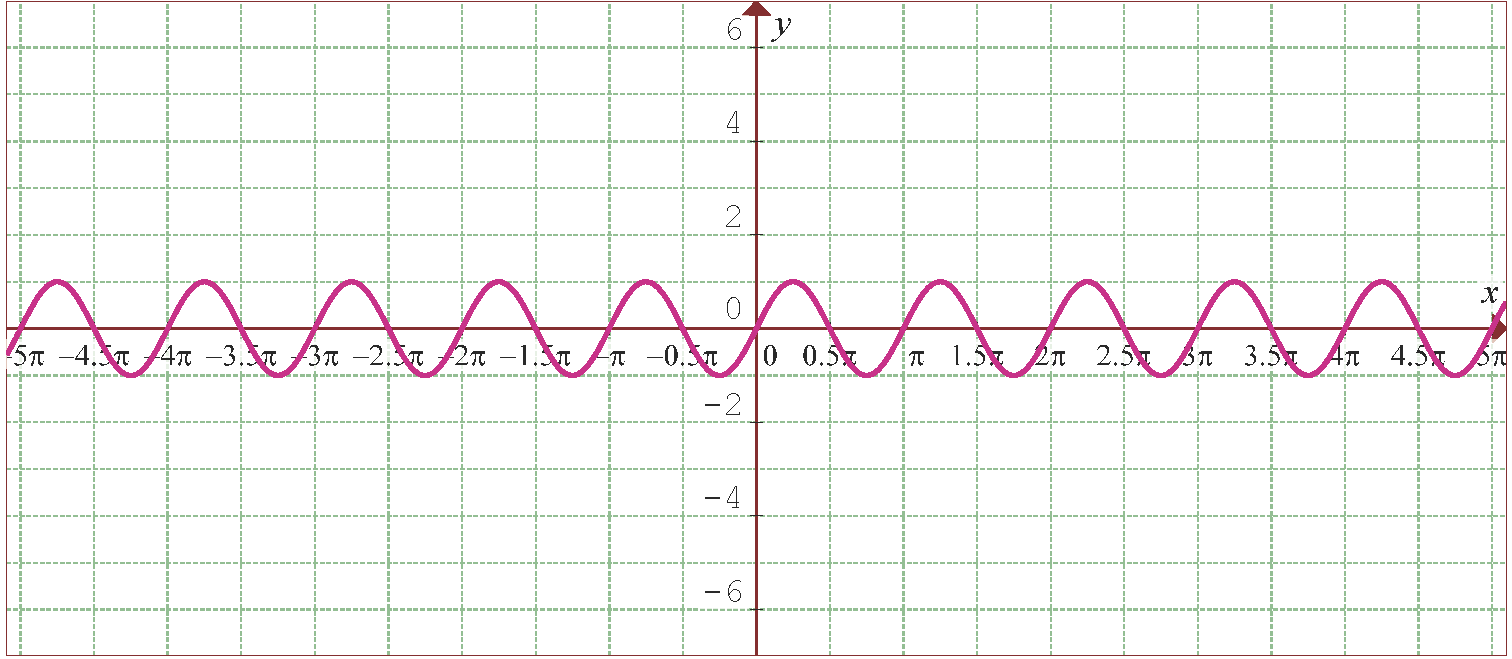
La siguiente Figura muestra la gráfica de la función  propuesta.
propuesta.
8 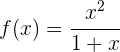
Comenzamos por encontrar la primera y la segunda derivada de la función dada:
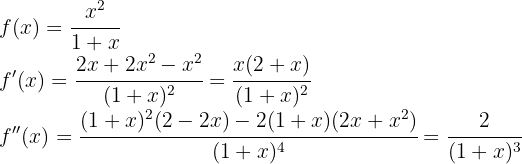
Ahora encontramos los puntos críticos  a través de la solución (o soluciones) de la ecuación
a través de la solución (o soluciones) de la ecuación 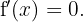
Tenemos entonces que

Las soluciones a esta ecuación son 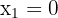 y
y 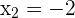 . Así, solo tenemos dos puntos críticos
. Así, solo tenemos dos puntos críticos
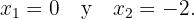
Finalmente, se evalúa  en el punto crítico
en el punto crítico  y determinar si
y determinar si  o
o  .
.
Tenemos entonces que

Entonces por el criterio de la segunda derivada, la función  tiene un mínimo local en
tiene un mínimo local en 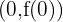 , es decir, en el punto
, es decir, en el punto

Ahora evaluamos en el segundo punto crítico:
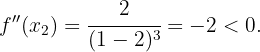
Entonces por el criterio de la segunda derivada, la función  tiene un máximo local en
tiene un máximo local en 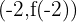 , es decir, en el punto
, es decir, en el punto 
La siguiente figura muestra la gráfica de la función  propuesta.
propuesta.

9 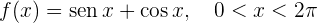
Comenzamos por encontrar la primera y la segunda derivada de la función dada:
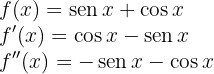
Ahora encontramos los puntos críticos  a través de la solución (o soluciones) de la ecuación
a través de la solución (o soluciones) de la ecuación 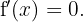
Tenemos entonces que
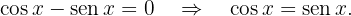
Las soluciones a esta ecuación, para 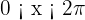 , son
, son 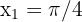 y
y 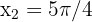 . Así, solo tenemos dos puntos críticos
. Así, solo tenemos dos puntos críticos
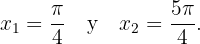
Finalmente, se evalúa  en el punto crítico
en el punto crítico  y determinar si
y determinar si  o
o  .
.
Tenemos entonces que
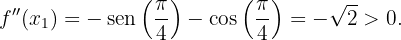
Entonces por el criterio de la segunda derivada, la función  tiene un máximo local en
tiene un máximo local en  , es decir, en el punto
, es decir, en el punto
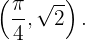
Ahora evaluamos en el segundo punto crítico:
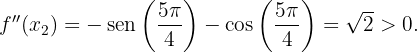
Entonces por el criterio de la segunda derivada, la función  tiene un mínimo local en
tiene un mínimo local en  , es decir, en el punto
, es decir, en el punto

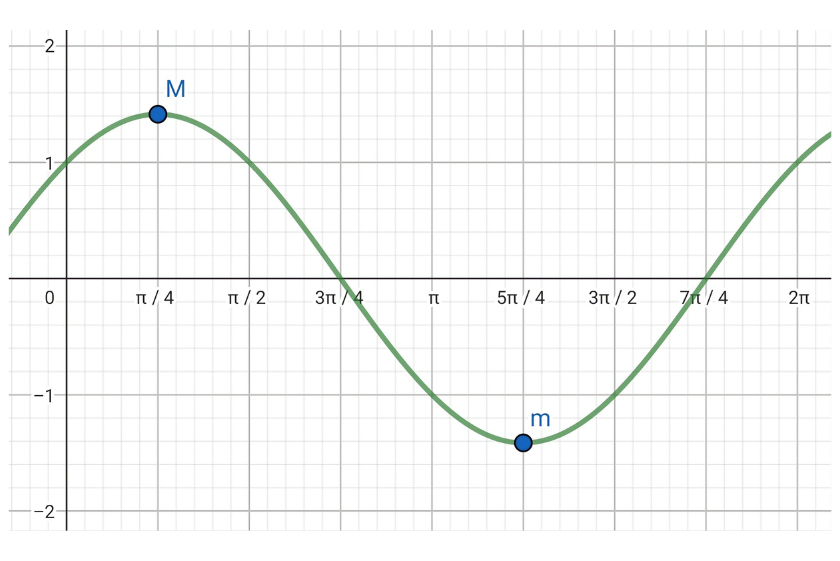
La siguiente figura muestra la gráfica de la función  propuesta.
propuesta.
10 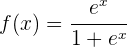
Comenzamos por encontrar la primera y la segunda derivada de la función dada:
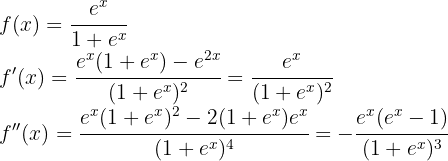
Ahora encontramos los puntos críticos  a través de la solución (o soluciones) de la ecuación
a través de la solución (o soluciones) de la ecuación 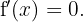
Tenemos entonces que
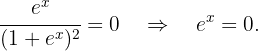
La solución a esta ecuación es 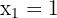 . Así, solo tenemos un punto crítico
. Así, solo tenemos un punto crítico
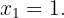
Finalmente, se evalúa  en el punto crítico
en el punto crítico  y determinar si
y determinar si  o
o  .
.
Tenemos entonces que
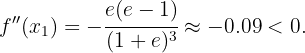
Entonces por el criterio de la segunda derivada, la función  tiene un máximo local en
tiene un máximo local en 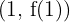 , es decir, en el punto
, es decir, en el punto

La siguiente figura muestra la gráfica de la función  propuesta.
propuesta.

Recuerda que si necesitas ayuda adicional, podrás encontrar el profesor de mates ideal para tu nivel en Superprof.



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Está mal la solución de la función inversa de f(x) = (2x+3)/x-1
Ya lo revise y no encuentro el error, podrías señalar en que está mal.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)