1 La cotización de las sesiones de una determinada sociedad, suponiendo que la Bolsa funciona todos los días de un mes de  días, responde a la siguiente ley:
días, responde a la siguiente ley:
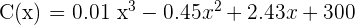
1 Determinar las cotizaciones máxima y mínima, así como los días en que ocurrieron, en días distintos del primero y del último.
2 Determinar los períodos de tiempo en el que las acciones subieron o bajaron.
1 Determinar las cotizaciones máxima y mínima, así como los días en que ocurrieron, en días distintos del primero y del último.
Derivamos
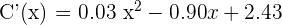
Igulamos la derivada a cero y hallamos las raíces de la ecuación
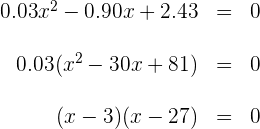
Las raíces son  y
y 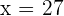
Calculamos la segunda derivada

Calculamos el signo que toman la raíces de la derivada primera
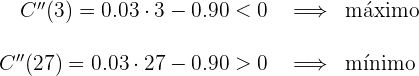
2 Determinar los períodos de tiempo en el que las acciones subieron o bajaron.
Formamos intervalos con los ceros de la derivada primera
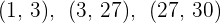
Tomamos un valor de cada intervalo, y hallamos el signo que tiene en la derivada primera:
Si el resultado es positivo, la función es creciente en ese intervalo.
Si el resultado es negativo, la función es decreciente en ese intervalo.

Del  al
al  , y del
, y del  al
al  las acciones subieron, y del
las acciones subieron, y del  al
al  bajaron.
bajaron.
¿Buscas clases particulares matematicas en Valencia?
2 Supongamos que el rendimiento  en
en 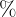 de un alumno en un examen de una hora viene dado por:
de un alumno en un examen de una hora viene dado por:
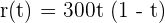 .
.
Donde 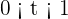 es el tiempo en horas. Se pide:
es el tiempo en horas. Se pide:
1 ¿En qué momentos aumenta o disminuye el rendimiento?
2 ¿En qué momentos el rendimiento es nulo?
3 ¿Cuando se obtiene el mayor rendimiento y cuál es?
1 ¿En qué momentos aumenta o disminuye el rendimiento?
Derivamos

Igulamos la derivada a cero y hallamos las raíces de la ecuación
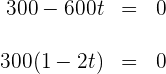
La raíz es 
Formamos intervalos con los ceros de la derivada primera

Tomamos un valor de cada intervalo, y hallamos el signo que tiene en la derivada primera:
Si el resultado es positivo, la función es creciente en ese intervalo.
Si el resultado es negativo, la función es decreciente en ese intervalo.

Así la función es creciente en 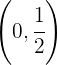 y decreciente en
y decreciente en 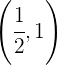 .
.
2 ¿En qué momentos el rendimiento es nulo?
El rendimiento es nulo cuando 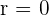 .
.
 .
.
Las raíces son 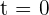 y
y 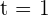 .
.
así el rendimiento es nulo al inicio y al final de la prueba.
3 ¿Cuando se obtiene el mayor rendimiento y cuál es?
Calculamos la segunda derivada
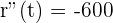
La segunda derivada siempre es negativa, por lo que  y se tiene un máximo
y se tiene un máximo
Calculamos la segunda coordenada del máximo
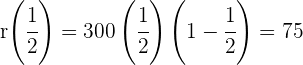
Así el mayor rendimiento se obtiene a la mitad de la prueba y es de 
¿Necesitas un profesor matematicas Madrid?
3Obtener la ecuación de la tangente a la gráfica de 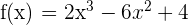 en su punto de inflexión.
en su punto de inflexión.
1 Calculamos la derivada
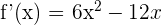
2 Calculamos la segunda derivada
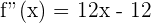
3 Igualamos la segunda derivada a cero para obtener el punto de inflexión
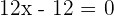
de donde obtenemos 
Calculamos la tercera derivada y evaluamos 
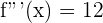

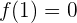
Así la función tiene un punto de inflexión en  .
.
4 Calculamos la recta tangente en el punto de inflexión, para lo cual requerimos la pendiente

Aplicando la fórmula punto pendiente se obtiene
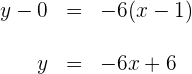
La recta tangente que pasa por el punto de inflexión es 
4 Determinar  y
y  para que la función
para que la función 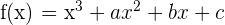 tenga un máximo para
tenga un máximo para 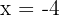 , un mínimo para
, un mínimo para  y tome el valor
y tome el valor  para
para  .
.
1 Calculamos la derivada
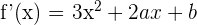
2 Como la función tiene un máximo en 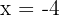 y un mínimo en
y un mínimo en  , entoces la derivada es cero en estos puntos. Sustituimos y obtenemos dos ecuaciones
, entoces la derivada es cero en estos puntos. Sustituimos y obtenemos dos ecuaciones
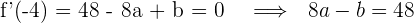

Sustituimos el valor de  en la primera ecuación y se obtiene
en la primera ecuación y se obtiene 
3 Como la función toma el valor  para
para 
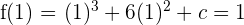
de donde obtenemos 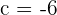 . Luego la función es
. Luego la función es
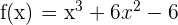
4 Calculamos la segunda y evaluamos los puntos críticos
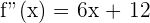
 , entonces tiene un máximo
, entonces tiene un máximo
 , entonces tiene un mínimo
, entonces tiene un mínimo
5 Determinar el valor de  y
y  para que la función
para que la función 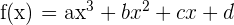 tenga un máximo en
tenga un máximo en  y un mínimo en
y un mínimo en  .
.
1 Calculamos la derivada
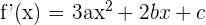
2 Como la función tiene un máximo en  y un mínimo en
y un mínimo en  , entonces la derivada es cero en estos puntos. Sustituimos y obtenemos dos ecuaciones
, entonces la derivada es cero en estos puntos. Sustituimos y obtenemos dos ecuaciones

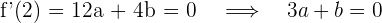
3 Como 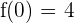 y
y 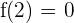 , se obtienen las ecuaciones
, se obtienen las ecuaciones

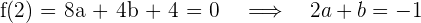
4 Resolvemos el sistema 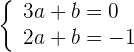
Obtenemos 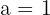 y
y  . Luego la función es
. Luego la función es

5 Calculamos la segunda y evaluamos los puntos críticos

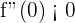 , entonces tiene un máximo
, entonces tiene un máximo
 , entonces tiene un mínimo
, entonces tiene un mínimo
6 Determinar el valor de 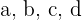 y
y  de modo que la curva
de modo que la curva 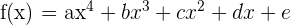 tenga un punto crítico en
tenga un punto crítico en  y un punto de inflexión con tangente de ecuación
y un punto de inflexión con tangente de ecuación  en
en  .
.
1 Calculamos la derivada
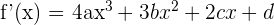
2 Como la función tiene un punto crítico en  , entonces la derivada es cero en este punto. Sustituimos y obtenemos la ecuación
, entonces la derivada es cero en este punto. Sustituimos y obtenemos la ecuación
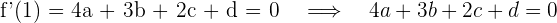
3 Como  y
y 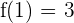 , se obtienen las ecuaciones
, se obtienen las ecuaciones

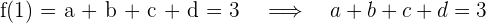
4 Calculamos la segunda derivada y evaluamos el punto de inflexión en ella

5 La derivada evaluada en cero coincide con la pendoente de la recta tangente en 

6 Resolvemos el sistema 
Obtenemos  y
y  . Luego la función es
. Luego la función es
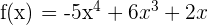
7 La curva 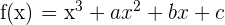 corta al eje de abscisas en
corta al eje de abscisas en  y tiene un punto de inflexión en
y tiene un punto de inflexión en 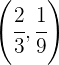 . Hallar
. Hallar  y
y  .
.
1 Calculamos la segunda derivada y evaluamos el punto de inflexión
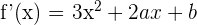
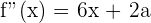
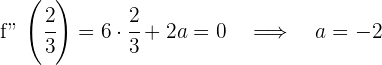
2 Evaluamos la función en el punto de inflexión y se obtiene

3 Como  , se obtiene la ecuación
, se obtiene la ecuación

4 Resolvemos el sistema 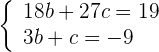
Obtenemos  y
y 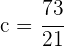 . Luego la función es
. Luego la función es

8 Dada la función:
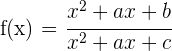
Calcula  y
y  , de modo que
, de modo que  tenga en
tenga en  un extremo local y que la curva pase por el origen de coordenadas.
un extremo local y que la curva pase por el origen de coordenadas.
1 Calculamos la derivada
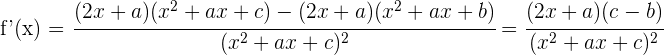
2 La derivada es cero en 
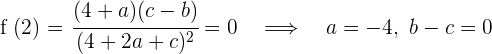
pero no se puede cumplir que 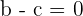 ya que la función sería
ya que la función sería 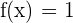 y no se cumple la condición de que la función pasa por el origen
y no se cumple la condición de que la función pasa por el origen
3 Como  y
y 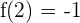 , se obtienen las ecuaciones
, se obtienen las ecuaciones

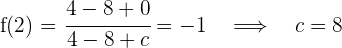
Luego la función es

9 Hallar  y
y  para qué la función:
para qué la función: 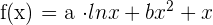 tenga extremos en los puntos
tenga extremos en los puntos  y
y  . Para esos valores de
. Para esos valores de  y
y  , ¿qué tipo de extremos tienen la función en
, ¿qué tipo de extremos tienen la función en  y en
y en  ?
?
1 Calculamos la derivada y evaluamos  y
y  , en estos puntos la derivada es cero ya que son puntos extremos
, en estos puntos la derivada es cero ya que son puntos extremos

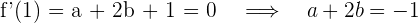
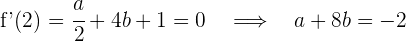
4 Resolvemos el sistema 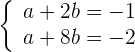
Obtenemos 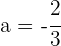 y
y 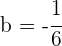 . Luego la función es
. Luego la función es
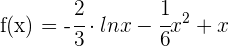
5 Calculamos la segunda derivada y evaluamos  y
y 
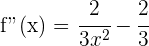
 , entonces se tiene un mínimo en
, entonces se tiene un mínimo en 
 , entonces se tiene un máximo en
, entonces se tiene un máximo en 
10 Determina las ecuaciones de la tangente y normal en su punto de inflexión a la curva: 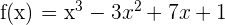 .
.
1 Calculamos la derivada
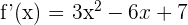
2 Calculamos la segunda derivada

3 Igualamos la segunda derivada a cero para obtener el punto de inflexión
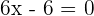
de donde obtenemos 
Calculamos la tercera derivada y evaluamos 
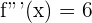
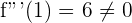
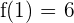
Así la función tiene un punto de inflexión en 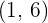 .
.
4 Calculamos la recta tangente en el punto de inflexión, para lo cual requerimos la pendiente
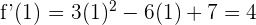
Aplicando la fórmula punto pendiente se obtiene
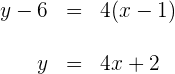
La recta tangente que pasa por el punto de inflexión es 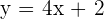
Aplicando la fórmula punto pendiente para la pendiente  de la recta normal, se obtiene
de la recta normal, se obtiene
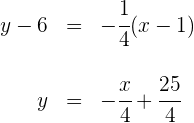
La recta normal que pasa por el punto de inflexión es 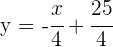
11 La cantidad  de manera acumulada en una máquina tragaperras durante un día es una ley del tipo:
de manera acumulada en una máquina tragaperras durante un día es una ley del tipo:
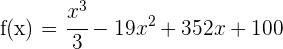
donde la variable  representa el tiempo en horas (de 0 a 24). Responde a las siguientes preguntas:
representa el tiempo en horas (de 0 a 24). Responde a las siguientes preguntas:
1 ¿Se queda alguna vez vacía de dinero la máquina?
2 Si se realiza la "caja" a las 24 horas. ¿Arroja ganancias para los dueños de la máquina?
3 ¿A qué hora la recaudación es máxima y a qué hora es mínima?
4 ¿Cuándo entrega el mayor premio?
1 Entre 0 y 24 la función es distinta de cero, por lo cual la máquina siempre tiene monedas.
Hay un mínimo absoluto en 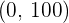 .
.
2 Si se realiza la "caja" a las 24 horas. ¿Arroja ganancias para los dueños de la máquina?
Ganancia: 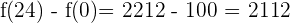
3 ¿A qué hora la recaudación es máxima y a qué hora es mínima?
Calculamos la derivada

Igualamos la derivada a cero
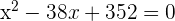
se obtiene  y
y 
4 Calculamos la segunda derivada y evaluamos  y
y 

 es un mínimo
es un mínimo
así, la recaudación es máxima a las 16 horas y es mínima a las 22 horas
5 ¿Cuándo entrega el mayor premio?
El mayor premio será igual al punto de inflexión
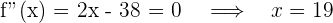

así, el mayor premio se entrega a las 19 horas
12 Sea 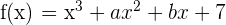 . Hallar
. Hallar  y
y  de manera que la gráfica de la función
de manera que la gráfica de la función  tenga para
tenga para  una inflexión, y cuya recta tangente en ese punto forme un ángulo de
una inflexión, y cuya recta tangente en ese punto forme un ángulo de  con el eje
con el eje  .
.
1 Calculamos la primera y segunda derivada
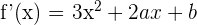
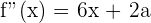
2 Como la función tiene un punto de inflexión en  , entonces la derivada es cero en este punto. Sustituimos y obtenemos
, entonces la derivada es cero en este punto. Sustituimos y obtenemos

3 Como la recta tangente en  forma un ángulo de
forma un ángulo de  y su pendiente es igual a la tangente de este ángulo, se tiene
y su pendiente es igual a la tangente de este ángulo, se tiene

Luego la función es

¿Buscas un profesor matematicas en Barcelona?



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3