Representar las siguientes funciones, estudiando los puntos siguientes
- Dominio
- Simetría
- Puntos de corte con los ejes
- Asíntotas
- Crecimiento y decrecimiento
- Máximos y mínimos
- Concavidad y convexidad
- Puntos de inflexión
1 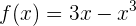
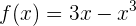 , es una función polinomial, entonces su dominio son todos los números reales, es decir,
, es una función polinomial, entonces su dominio son todos los números reales, es decir, 
Simetría
Para revisar la simetría comenzamos por evaluar la función en 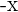 , y tendremos 3 posibles casos,
, y tendremos 3 posibles casos,
1 Una función par si  ,
,
2 Una función impar si  ,
,
3 o no aplica si no regresamos a la función original.
En este caso
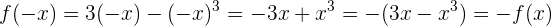
Por tanto, tenemos simetría respecto al origen, es decir, función impar
Puntos de corte con los ejes
Puntos de corte con  :
:
Tenemos corte en este eje si 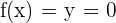 , entonces, comenzamos igualando a cero
, entonces, comenzamos igualando a cero
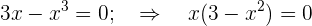
Por tanto obtenemos cero si
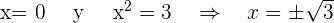
De aquí tendremos que los puntos de corte del eje  son:
son:

Punto de corte con  :
:
Tenemos puntos de corte en este eje si  , entonces:
, entonces:
 .
.
Por lo tanto el punto de corte con el eje  es:
es:
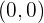
Asíntotas
Para encontrar las asíntotas, tendríamos que encontrar un punto  tal que
tal que  ,
,
En este caso tenemos una función polinomial la cuál no tiene asíntotas.
Crecimiento y decrecimiento
Para saber si una función es creciente o decreciente en un punto, debemos de encontrar los puntos críticos, es decir, donde la derivada se hace cero. Calculamos la derivada 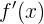
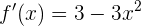
Vamos a calcular los puntos críticos

Ahora vamos a revisar que signo tiene la función al segmentar el dominio en  y
y  :
:

Entonces la función es creciente en el intervalo 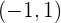 y decreciente en
y decreciente en 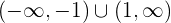
Para encontrar los mínimos y máximos, evaluamos los puntos críticos encontrados anteriormente en la segunda derivada. Si es positiva, entonces tenemos un mínimo, si es negativa entonces tenemos un máximo.
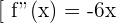
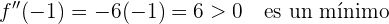

Entonces tenemos un mínimo en 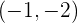 , y un máximo en
, y un máximo en 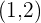
Concavidad y convexidad
Para revisar la concavidad y conexidad usamos la segunda derivada cuando se hace cero y revisamos los intervalos donde la función es positiva y negativa, si es positiva entonces es convexa y si es negativa, entonces es cóncava.
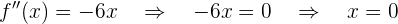
y en los intervalos

Entonces la función es convexa en el intervalo 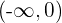 y cóncava en
y cóncava en 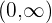
Puntos de inflexión
Se tiene un punto de inflexión si en un punto  ,
,

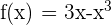
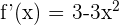

Ahora evaluamos el único punto donde la segunda derivada se hace cero
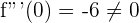
Cómo el resultado es diferente de cero entonces tenemos un punto de inflexión en 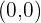 .
.
Representación gráfica

2 

Simetría
Observemos que
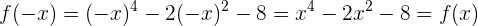
Por tanto, tenemos simetría respecto al eje  , es decir, la función es par.
, es decir, la función es par.
Puntos de corte con los ejes
Puntos de corte con  :
:
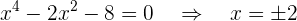
Entonces, los puntos de corte son

Puntos de corte con  :
:
Notemos que
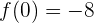
entonces el punto de corte es

Asíntotas
No tiene asíntotas.
Crecimiento y decrecimiento
Calculamos los puntos critimos:
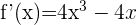
igualamos a cero
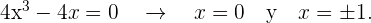
Ahora revisamos el signo al segmentar el dominio:




por lo tanto es creciente en  y decreciente en
y decreciente en 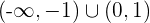
Evaluando los puntos críticos encontrados en la segunda derivada  obtenemos que
obtenemos que
Los puntos mínimos son
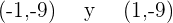
Como punto máximo tenemos a
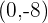
Concavidad y convexidad
Buscamos los puntos donde la segunda derivada se hace cero
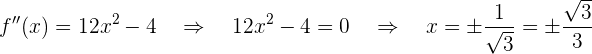
Notemos que
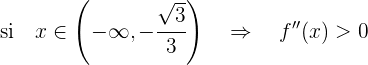


por lo tanto es convexa en 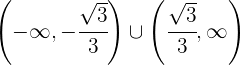 y concava en
y concava en 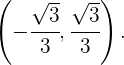
Puntos de inflexión
Calculando la tercera derivada concluimos que los puntos de inflexion son
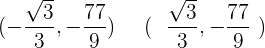
Representación gráfica

3 
Eliminamos el punto donde se hace cero el denominador
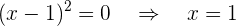
por tanto
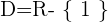
Simetría
Notemos que

es decir, no presenta simetría.
Puntos de corte con los ejes
Puntos de corte con 
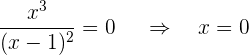
Entonces, el punto de corte es 
Punto de corte con 
Tenemos que
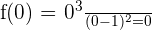
entonces el punto de corte es
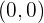
Asíntotas
Asíntota horizontal:
Las asíntotas horizontales son rectas horizontales a las cuales la función se va acercando indefinidamente. Las asíntotas horizontales son rectas de ecuación: 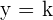 .
.

Notemos que

Entonces no tiene asíntota horizontal.
Asíntotas verticales:
Las asíntotas verticales son rectas verticales a las cuales la función se va acercando indefinidamente sin llegar nunca a cortarlas. Las asíntotas verticales son rectas de ecuación: 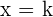 .
.

Notemos que

entonces

Asíntota oblicua:
Las asíntotas oblicuas son rectas de ecuación:

donde

Sólo hallaremos las asíntotas oblicuas cuando no haya asíntotas horizontales.
En este caso:


Entonces la asíntota oblicua tiene ecuación :
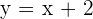
Crecimiento y decrecimiento
Primero encontramos los puntos críticos
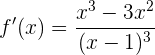
igualando a cero

tendremos que los puntos críticos son

Revisamos los signos al segmentar el dominio




entonces
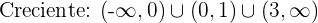
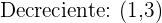
Evaluando los puntos críticos encontrados en la segunda derivada obtenemos que
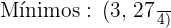
Concavidad y convexidad
Calculando la segunda derivada y encontrando donde se hace cero

Evaluando en los intervalos cercanos

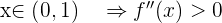
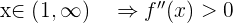
por lo tanto es convexa en  y concava en
y concava en 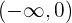
Puntos de inflexión
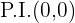
Representación gráfica
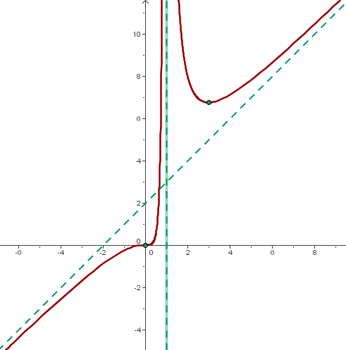
4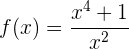
Eliminamos el punto donde el denominador se hace cero

Simetría
Notemos que
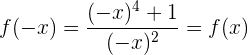
Entonces tenemos simetría respecto al eje  , es decir, se trata de una función par.
, es decir, se trata de una función par.
Puntos de corte con los ejes
Puntos de corte con  :
:
Igualamos a cero y obtenemos
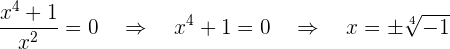
Por tanto, no hay puntos de corte con el eje 
Punto de corte con  :
:
Similarmente
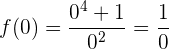
Por tanto, no hay puntos de corte con el eje 
Asíntotas
Asíntota horizontal:

Es decir, no hay asíntota horizontal
Asíntotas verticales:

Asíntota oblicua:
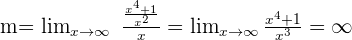
Es decir, no tiene.
Crecimiento y decrecimiento
Observemos que

de aqui



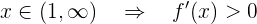
Por lo tanto la función será creciente en  y decreciente en
y decreciente en 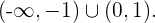
Ademas, los puntos mínimos estan dado por  y
y 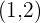
Concavidad y convexidad
Observemos que

entonces
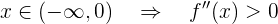
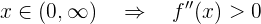
De aqui concluimos que la función es convexa en 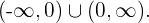
Puntos de inflexión
No hay punto de inflexión.
Representación gráfica

5 
Eliminamos el mundo donde el denominador se anula

Simetría
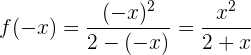
No presenta simetría
Puntos de corte con los ejes
Puntos de corte con  :
:
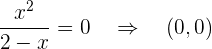
Punto de corte con  :
:

Asíntotas
Asíntota horizontal:
Notemos que
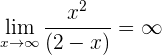
Entonces, no tiene.
Asíntotas verticales:

Asíntota oblicua


entonces

Crecimiento y decrecimiento
Encontramos puntos críticos

Evaluando en los intervalos

Es decir, tendremos que es creciente en 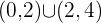 y decreciente en
y decreciente en  .
.
Evaluamos los puntos críticos encontrados en la segunda derivada, para encontrar los mínimos y máximos.
Tendremos que  es un minimo y
es un minimo y 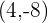 un máximo.
un máximo.
Concavidad y convexidad
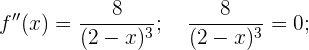
Puesto que no tenemos solución, dividiremos los intervalos del dominio a partir del 2 que no pertenece al dominio.
Obteniendo

Por tanto, tenemos que de 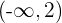 convexa y de
convexa y de 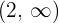 concava.
concava.
Puntos de inflexión
No hay punto de inflexión.
Representación gráfica

¿Buscas clases particulares matematicas? ¡Encuéntralas en Superprof!
6 

Simetría
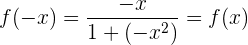
Tenemos simetría respecto al origen, es decir, se trata de una función impar.
Puntos de corte con los ejes
Punto de corte con  :
:
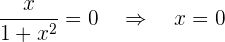
entonces el punto de corte es 
Punto de corte con  :
:
Tenemos
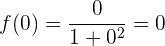
entonces el punto de corte es
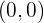
Asíntotas
Asíntota horizontal:

No tiene asíntotas verticales ni oblicuas.
Crecimiento y decrecimiento
Encontramos los puntos críticos

Revisamos el signo tiene la función al segmentar el dominio

De donde tenemos que la función es creciente de  y decreciente en
y decreciente en  .
.
Y evaluando los puntos criticos en la segunda derivada, tendremos que
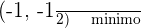
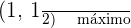
Concavidad y convexidad
Calculamos los puntos donde se hace cero la segunda derivada
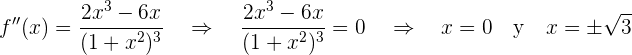
Revisamos el signo en los intervalos

Por tanto, tenemos que la función es convexa en  y es cóncava en
y es cóncava en 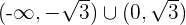 .
.
Puntos de inflexión
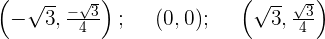
Representación gráfica
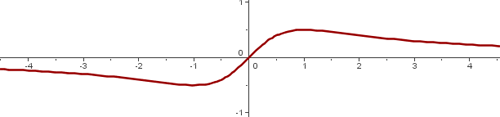
7 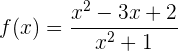

Simetría
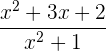
No presenta simetría
Puntos de corte con los ejes
Puntos de corte con  :
:
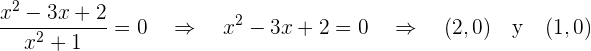
Punto de corte con  :
:

Asíntotas
Asíntota horizontal:

No hay asíntotas verticales ni oblicuas.
Crecimiento y decrecimiento
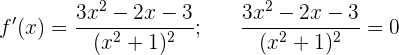
entonces

Revisamos el signo al segmentar el dominio de la función

Por tanto tenemos que es creciente de 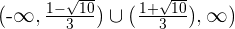 y decreciente de
y decreciente de 
Evaluando los puntos críticos en la segunda derivada encontramos que


Con los datos obtenidos representamos:

Si buscas un profesor de matematicas online, ¡está en Superprof!
8 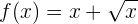
Puesto que se esta calculando la raiz de " " en la funcion tendremos que
" en la funcion tendremos que

Simetría
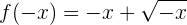
No presenta simetría.
Puntos de corte con los ejes
Puntos de corte con  :
:
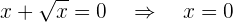
por lo que el punto de corte es
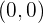
Punto de corte con  :
:

por lo que el punto de corte es

Asíntotas
No tiene asíntotas.
Crecimiento y decrecimiento
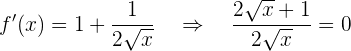
Por lo tanto, los puntos críticos son
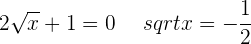
Puesto que no tiene solución, solo consideramos el intervalo del dominio

Es decir, es una función creciente.
Máximo y mínimos
No existen extremos locales.
Concavidad y convexidad
Calculamos la segunda derivada y la igualamos a cero
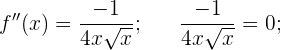
Al no tener solución, tomamos el intervalo del dominio, obteniendo

Por lo que es una funcion concava.
Puntos de inflexión
No hay punto de inflexión.
Representación gráfica

9 
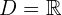
Simetría
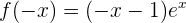
No presenta simetría.
Puntos de corte con los ejes
Puntos de corte con  :
:
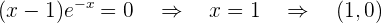
Punto de corte con  :
:
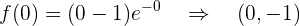
Asíntotas
Asíntota horizontal:

No hay asíntotas verticales ni oblicuas.
Crecimiento y decrecimiento

verificando el signo

De donde deducimos que la función es creciente de 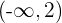 y decreciente de
y decreciente de 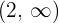
Evaluando los puntos críticos en la segunda derivada, encontramos que
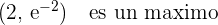
Concavidad y convexidad
Calculamos la segunda derivada y encontramos los puntos que la anulan

Se segmenta el dominio en  y observando el signo de la segunda derivada en estos intervalos
y observando el signo de la segunda derivada en estos intervalos

Por tanto, la función em el intervalo  es convexa y en el intervalo
es convexa y en el intervalo  es concava.
es concava.
Puntos de inflexión
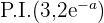
Representación gráfica
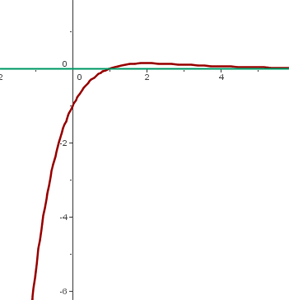
10 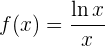
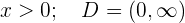
Simetría

No presenta simetría.
Puntos de corte con los ejes
Puntos de corte con  :
:

es decir,  y el punto de corte sería
y el punto de corte sería
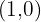
Punto de corte con  :
:

No corta con el eje 
Asíntotas
Asíntota horizontal:
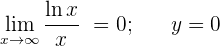
Asíntotas verticales
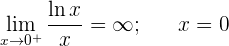
Crecimiento y decrecimiento
Calculamos puntos criticos

obteniendo como punto critico  . Entonces
. Entonces

por tanto la función es creciente de 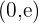 y decreciente de
y decreciente de  . Encontramos un máximo en
. Encontramos un máximo en  .
.
Concavidad y convexidad
Igualando la segunda derivada a cero
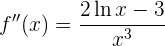

Segmentando el dominio y observando el signo de la segunda derivada concluimos que la función es convexa de  y cóncava de
y cóncava de  .
.
Representación gráfica
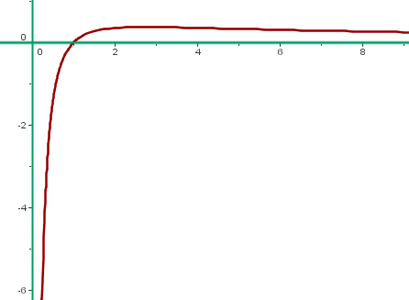
¿Quieres aprender a tu ritmo con un profesor particular? Encuentra el curso matematicas que mejor te convenga en Superprof.



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Está mal la solución de la función inversa de f(x) = (2x+3)/x-1
Ya lo revise y no encuentro el error, podrías señalar en que está mal.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Cuántas fórmulas tiene la tabla de valor