
Gráfica de una función
La gráfica de una función está formada por el conjunto de puntos 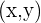 cuando
cuando  varía en el dominio
varía en el dominio  .
.
Gráfica </p >
</p >
Para representarla calcularemos aquellos puntos o intervalos donde la función tiene un comportamiento especial, que determinaremos mediante el estudio de los siguientes apartados:
1. Dominio de la función.
2. Simetría
3. Periodicidad
4. Puntos de corte con los ejes.
5. Asíntotas
6. Ramas parabólicas
7. Crecimiento y Decrecimiento
8. Máximos y mínimos
9. Concavidad y convexidad
10. Puntos de inflexión
¿Cómo representar funciones?
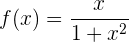
Dominio
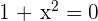
No tiene solución

Simetría
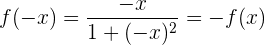
Simetría respecto al origen, es decir, la función es impar.
Puntos de corte
Punto de corte con  :
:

Punto de corte con  :
:
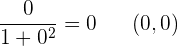
Asíntotas
Asíntota horizontal

No tiene asíntotas verticales ni oblicuas.
Crecimiento y decrecimiento

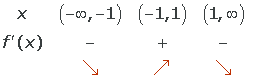
Creciente 
Decreciente 
Máximos y mínimos
Candidatos a extremos:  y
y 
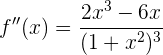
 hay un mínimo en
hay un mínimo en  </p >
</p >
Mínimo 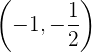
 hay un máximo en
hay un máximo en 
Máximo 
Concavidad y convexidad

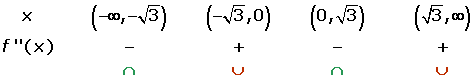
Convexa 
Cóncava 
Puntos de inflexión
 </p >
</p >
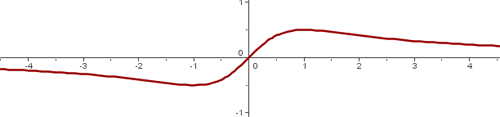
Representación gráfica













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3