Temas

Optimizacion en figuras geométricas
1 Obtener el triángulo isósceles de área máxima inscrito en un círculo de radio 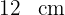 .
.
1 Representamos graficamente los datos
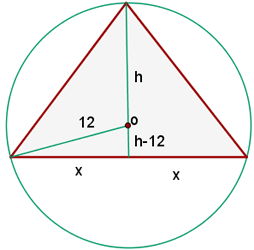
2Función a optimizar es la que representa el área del triángulo isósceles:
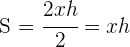
3Relacionamos las variables:
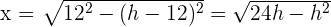
4Sustituimos en la función:

5Derivamos, igualamos a cero y calculamos las raíces

Igualamos a cero (en este caso basta solo el numerador) y calculamos las raíces

Sustituimos en la relación de  y
y  para obtener
para obtener
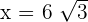
Luego la base es 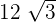
y el lado es
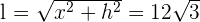
6Realizamos la derivada segunda para comprobar el resultado obtenido
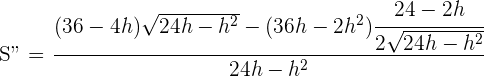
Al evaluar  se obtiene
se obtiene 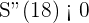
De este modo, el criterio de la segunda derivada afirma que "si la segunda derivada es menor que cero (negativa), entonces la función tiene un máximo relativo. En conclusión, para la altura máxima de  , existe un máximo relativo
, existe un máximo relativo
2 Un triángulo isósceles de perímetro 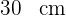 , gira alrededor de su altura
, gira alrededor de su altura
engendrando un cono.
¿Qué valor debe darse a la base para que el volumen del cono sea máximo?
1 Representamos graficamente los datos

2Función a optimizar es la que representa el área del triángulo isósceles:

3Relacionamos las variables:
Aplicamos el teorema de Pitágoras
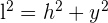
Aplicamos el perímetro

Igualamos ambas expresiones y obtenemos

4Sustituimos en la función:
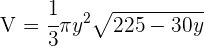
5Derivamos, igualamos a cero y calculamos las raíces
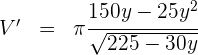
Igualamos a cero (en este caso basta solo el numerador) y calculamos las raíces
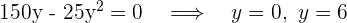
Luego la base es 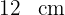
6Realizamos la derivada segunda para comprobar el resultado obtenido
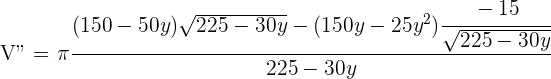
Al evaluar 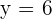 se obtiene
se obtiene 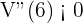
De este modo, el criterio de la segunda derivada afirma que "si la segunda derivada es menor que cero (negativa), entonces la función tiene un máximo relativo. En conclusión, para el radio máximo de  , existe un máximo relativo
, existe un máximo relativo
3 Hallar las dimensiones del mayor rectángulo inscrito en un triángulo isósceles que tiene por base 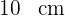 y por altura
y por altura 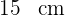 .
.
1 Representamos graficamente los datos
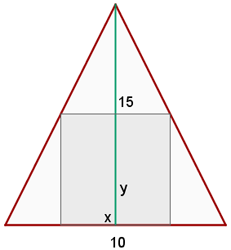
2Función a optimizar

3Relacionamos las variables: al tener dos triángulos semejantes se obtiene

Aplicamos el perímetro

4Sustituimos en la función:
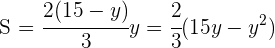
5Derivamos, igualamos a cero y calculamos las raíces
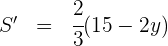
Igualamos a cero y calculamos las raíces
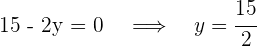
Luego la base es 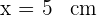
6Realizamos la derivada segunda para comprobar el resultado obtenido

Al evaluar  se obtiene
se obtiene 
De este modo, el criterio de la segunda derivada afirma que "si la segunda derivada es menor que cero (negativa), entonces la función tiene un máximo relativo. En conclusión, para 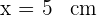 y
y  , existe un máximo relativo
, existe un máximo relativo
4 Un sector circular tiene un perímetro de  .
.
Calcular el radio y la amplitud del sector de mayor área.
1 Representamos graficamente los datos
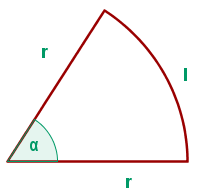
2Función a optimizar
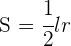
3Relacionamos las variables:

4Sustituimos en la función:
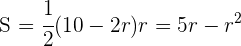
5Derivamos, igualamos a cero y calculamos las raíces
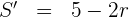
Igualamos a cero y calculamos las raíces

Luego 
6Realizamos la derivada segunda para comprobar el resultado obtenido
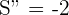
Al evaluar 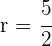 se obtiene
se obtiene 
De este modo, el criterio de la segunda derivada afirma que "si la segunda derivada es menor que cero (negativa), entonces la función tiene un máximo relativo. En conclusión, para 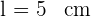 ,
, 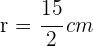 y
y  , existe un máximo relativo
, existe un máximo relativo
Optimización para el ahorro de material
1 Se pretende fabricar una lata de conserva cilíndrica (con tapa) de  litro de capacidad.
litro de capacidad.
¿Cuáles deben ser sus dimensiones para que se utilice el mínimo posible de metal?
1Función a optimizar

2Relacionamos las variables:
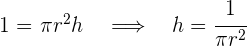
3Sustituimos en la función:

4Derivamos, igualamos a cero y calculamos las raíces

Igualamos a cero y calculamos las raíces
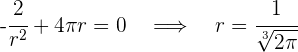
Luego 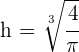
5Realizamos la derivada segunda para comprobar el resultado obtenido

Al evaluar 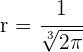 se obtiene
se obtiene 
De este modo, el criterio de la segunda derivada afirma que "si la segunda derivada es mayor que cero (positiva), entonces la función tiene un mínimo relativo. En conclusión, para 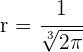 y
y 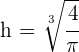 , existe un mínimo relativo
, existe un mínimo relativo
2 Se tiene un alambre de 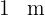 de longitud y se desea dividirlo en dos trozos para formar con uno de ellos un círculo y con el otro un cuadrado.
de longitud y se desea dividirlo en dos trozos para formar con uno de ellos un círculo y con el otro un cuadrado.
Determinar la longitud que se ha de dar a cada uno de los trozos para que la suma de las áreas del círculo y del cuadrado sea mínima.
1Función a optimizar

2Relacionamos las variables:
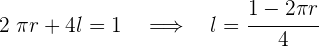
3Sustituimos en la función:
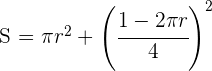
4Derivamos, igualamos a cero y calculamos las raíces
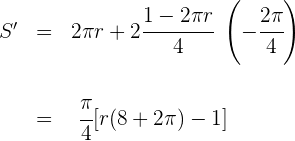
Igualamos a cero y calculamos las raíces
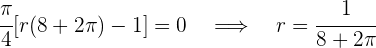
Luego el trozo del círculo es 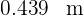 y el trozo del cuadrado es
y el trozo del cuadrado es 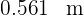
5Realizamos la derivada segunda para comprobar el resultado obtenido
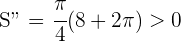
De este modo, el criterio de la segunda derivada afirma que "si la segunda derivada es mayor que cero (positiva), entonces la función tiene un mínimo relativo.
3 Hallar las dimensiones que hacen mínimo el coste de un contenedor que tiene forma de paralelepípedo rectangular sabiendo que su volumen ha de ser 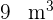 , su altura
, su altura 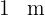 y el coste de su construcción por
y el coste de su construcción por  es de
es de  € para la base;
€ para la base;  para la tapa y
para la tapa y  para cada pared lateral.
para cada pared lateral.
1 Representamos graficamente los datos

2Función a optimizar

3Relacionamos las variables
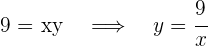
4Sustituimos en la función:
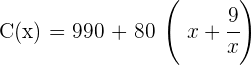
5Derivamos, igualamos a cero y calculamos las raíces
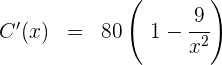
Igualamos a cero y calculamos las raíces

Luego 
6Realizamos la derivada segunda para comprobar el resultado obtenido
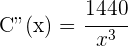
Al evaluar  se obtiene
se obtiene 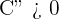
De este modo, el criterio de la segunda derivada afirma que "si la segunda derivada es mayor que cero, entonces la función tiene un mínimo relativo.
Diversos ejercicios sobre optimización
1 Descomponer el número  en dos sumandos tales que el quíntuplo del cuadrado del primero más el séxtuplo del cuadrado del segundo sea un mínimo.
en dos sumandos tales que el quíntuplo del cuadrado del primero más el séxtuplo del cuadrado del segundo sea un mínimo.
1Función a optimizar

2Relacionamos las variables:

3Sustituimos en la función:

4Derivamos, igualamos a cero y calculamos las raíces
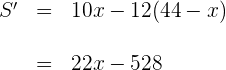
Igualamos a cero y calculamos las raíces

Luego 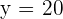
5Realizamos la derivada segunda para comprobar el resultado obtenido
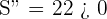
De este modo, el criterio de la segunda derivada afirma que "si la segunda derivada es mayor que cero (positiva), entonces la función tiene un mínimo relativo.
2 Recortando convenientemente en cada esquina de una lámina de cartón de dimensiones 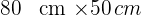 un cuadrado de lado
un cuadrado de lado  y doblando convenientemente (véase figura), se construye una caja.
y doblando convenientemente (véase figura), se construye una caja.
Calcular  para que volumen de dicha caja sea máximo.
para que volumen de dicha caja sea máximo.
1 Representamos graficamente los datos
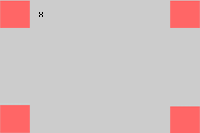
2Función a optimizar
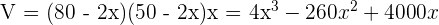
3Derivamos, igualamos a cero y calculamos las raíces
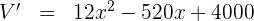
Igualamos a cero y calculamos las raíces

pero 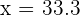 no es válida ya que
no es válida ya que 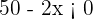
4Realizamos la derivada segunda para comprobar el resultado obtenido
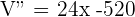
Al evaluar 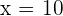 se obtiene
se obtiene 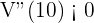
De este modo, el criterio de la segunda derivada afirma que "si la segunda derivada es menor que cero, entonces la función tiene un máximo relativo.
3 Una hoja de papel debe tener 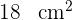 de texto impreso, márgenes superior e inferior de
de texto impreso, márgenes superior e inferior de  de altura y márgenes laterales de
de altura y márgenes laterales de 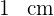 de anchura.
de anchura.
Obtener razonadamente las dimensiones que minimizan la superficie del papel.
1 Representamos graficamente los datos

2Función a optimizar

3Relacionamos las variables:
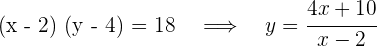
4Sustituimos en la función:
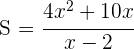
5Derivamos, igualamos a cero y calculamos las raíces

Igualamos a cero (basta solo el numerador) y calculamos las raíces
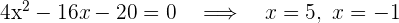
pero  no es válida
no es válida
6Realizamos la derivada segunda para comprobar el resultado obtenido
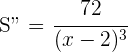
Al evaluar  se obtiene
se obtiene 
De este modo, el criterio de la segunda derivada afirma que "si la segunda derivada es mayor que cero, entonces la función tiene un mínimo relativo.
Optimización para producción y ganancias
El beneficio neto mensual, en millones de euros, de una empresa que fabrica autobuses
viene dado por la función:
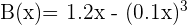
donde  es el número de autobuses fabricados en un mes.
es el número de autobuses fabricados en un mes.
1 Calcula la producción mensual que hacen máximo el beneficio.
2 El beneficio máximo correspondiente a dicha producción.
1Función a optimizar
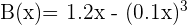
2Derivamos, igualamos a cero y calculamos las raíces

Igualamos a cero y calculamos las raíces
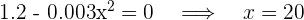
3Realizamos la derivada segunda para comprobar el resultado obtenido
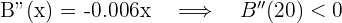
De este modo, el criterio de la segunda derivada afirma que "si la segunda derivada es menor que cero, entonces la función tiene un máximo relativo.
El beneficio máximo correspondiente a dicha producción

Problema de optimización en la huerta
Una huerta tiene actualmente  árboles, que producen
árboles, que producen  frutos cada uno.
frutos cada uno.
Se calcula que por cada árbol adicional plantado, la producción de cada árbol disminuyeen  frutos.
frutos.
Calcular:
1 La producción actual de la huerta.
2 La producción que se obtendría de cada árbol si se plantan  árboles más.
árboles más.
3 La producción a la que ascendería el total de la huerta si se plantan  árboles más.
árboles más.
4 ¿Cuál debe ser el número total de árboles que debe tener la huerta para qué la
producción sea máxima?
1 La producción actual de la huerta.
Producción actual: 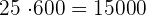 frutos.
frutos.
2 La producción que se obtendría de cada árbol si se plantan  árboles más.
árboles más.
Si se plantan  árboles más, la producción de cada árbol será:
árboles más, la producción de cada árbol será:  .
.
3 La producción a la que ascendería el total de la huerta si se plantan  árboles más.
árboles más.
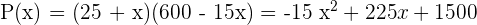
4 ¿Cuál debe ser el número total de árboles que debe tener la huerta para qué la producción sea máxima?
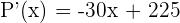
Igualamos la derivada a cero
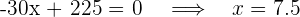
Calculamos la segunda derivada

La producción será máxima si la huerta tiene  ó
ó 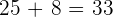 árboles
árboles













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3