
Pasos para la resolución de problemas
1 Se plantea la función que hay que maximizar o minimizar.
2 Se plantea una ecuación que relacione las distintas variables del problema, en el caso de que haya más de una variable.
3 Se despeja una variable de la ecuación y se sustituye en la función de modo que nos quede una sola variable.
4 Se deriva la función y se iguala a cero, para hallar los extremos locales.
5 Se realiza la 2ª derivada para comprobar el resultado obtenido.
Ejemplo de función optimizada
De todos los triángulos isósceles de 12 m de perímetro, hallar los lados del que tome área máxima.
1 El área del triángulo isósceles es la función a maximizar

2 Planteamos la función que tenemos que maximizar
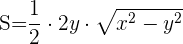
3 Dejamos una sola variable, para esto despejamos la ecuación del perímetro y la sustituimos en la del área

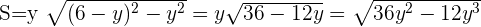
4 Derivamos, igualamos a cero y calculamos las raíces.
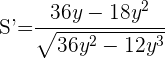
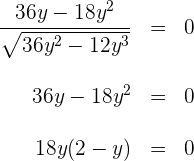
Los extremos locales son

5 Realizamos la 2ª derivada para comprobar el resultado obtenido. Sustituimos por 2, ya que la solución 0 la descartamos porque no hay un triángulo cuyo lado sea cero
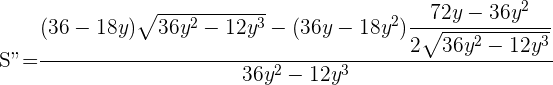
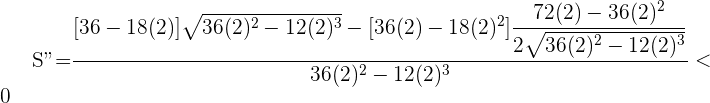
Por lo que queda probado que en 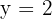 hay un máximo.
hay un máximo.
La base> mide 4 m y los lados oblicuos también miden 4 m, por lo que el triángulo de área máxima sería un triángulo equilátero.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3