Si 
y 
son derivables en 
1 
es convexa en
2
es cóncava en
Hemos tomado el criterio de que el valle tiene forma convexa y la montaña forma cóncava.
Es posible encontrar textos en los que se define la concavidad y la convexidad de manera opuesta, usando el criterio de que el valle tiene forma cóncava y la montaña forma convexa.
Pero esta definición que damos no sólo alude a un criterio visual que puede ser confuso desde el punto de vista del observador, sino que podemos dar una definición más precisa:
Una función es cóncava en un intervalo de su dominio cuando:
Dados dos puntos cualesquiera de dicho intervalo 
y 
, el segmento que une los puntos 
y 
siempre queda por debajo de la gráfica.
Una función es convexa en un intervalo de su dominio cuando:
Dados dos puntos cualesquiera de dicho intervalo y , el segmento que une los puntos y siempre queda por encima de la gráfica.
Intervalos de concavidad y convexidad
Estudiar los intervalos la concavidad y la convexidad de la función:
Para estudiar la concavidad y la convexidad, efectuaremos los siguientes pasos:
1 Hallamos la derivada segunda y calculamos sus raíces.
2 Formamos intervalos abiertos con los ceros (raíces) de la derivada segunda y los puntos de discontinuidad (si los hubiese).
3 Tomamos un valor de cada intervalo, y hallamos el signo que tiene en la derivada segunda.
Si 
, entonces 
es convexa
Si 
, entonces es cóncava
Del intervalo 
tomamos 
, por ejemplo
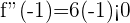es cóncava
Del intervalo 
tomamos 
, por ejemplo
es convexa
4 Escribimos los intervalos:
Convexidad:
Concavidad:
Ejemplos
1 
En primer lugar calculamos el dominio para saber donde está definida la función
Así el dominio es
Hallamos la derivada primera
Hallamos la segunda derivada
Igualamos a cero y hallamos las raíces de la ecuación
Formamos intervalos con los ceros de la derivada segunda y con los puntos de discontinuidad
Sustituimos un valor de cada intervalo en la función
Si el resultado es positivo, la función es convexa en ese intervalo
Si el resultado es negativo, la función es concava en ese intervalo
Convexa: 
Cóncava
2
Hallamos la derivada primera
Hallamos la segunda derivada
Igualamos a cero y hallamos las raíces de la ecuación
Convexa: 
Cóncava 
Punto de inflexión 
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
me pueden ayudar encontrar la derivada de : y=7 elevado a la 4 + e elevado a la x-4 – ln X + 100
Excelente contenido. Creo es posible mejorar el contenido para que sea más didáctico con más ejemplos, partiendo de lo elemental a lo complejo, para que el texto pueda ser más entendible para estudiantes de secundaria en Costa Rica.
Excelente artículo y muy dinámico.
Agradecemos tu comentario, la verdad estamos trabajando mucho para lograr tener las mejores explicaciones para que sea mas entendible al publico y para ello lo que ustedes recomienden nos ayuda en gran forma, esperamos que en un futuro seamos mejores siguiendo sus sugerencias, otra vez gracias.
Hola: El últipo ejercicio de aplicación me parece que es incorrecto ya que no está obteniendo la derivada del volumen del cono
Hola si te refieres al triángulo que gira, si se derivo el volumen, si estoy equivocado por favor indícamelo.
la pagina mas hermosa que he encontrado bien definida y completa, tendremos algo similar para integrales?
Hola que bueno que te guste la pagina, y si tenemos el tema de integrales tenemos por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/calculo/integrales/ejercicios-resueltos-de-integrales-por-sustitucion.html» esta pagina y otras mas para que las explores.
Está bien la explicación. Pero falta cuando la segunda derivada es igual a cero, que no aplicaría ese criterio.
Hola, que bueno que te gusten las explicaciones, en cuanto a la segunda derivada igualada a cero sirve para encontrar los puntos de inflexión, en cuanto el criterio podrías mencionar su nombre por favor.
Y=X ELEVADA ALA TRES -4X+5