1La relación entre la distancia recorrida en metros por un móvil y el tiempo en segundos es  . Calcular:
. Calcular:
a la velocidad media entre 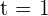 y
y  .
.
b La velocidad instantánea en 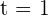 .
.
La relación entre la distancia recorrida en metros por un móvil y el tiempo en segundos es  . Calcular:
. Calcular:
a la velocidad media entre 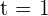 y
y  .
.

b La velocidad instantánea en 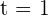 .
.

2Debido a unas pésimas condiciones ambientales, una colonia de un millón de bacterias no comienza su reproducción hasta pasados dos meses. La función que representa la población de la colonia al variar el tiempo (expresado en meses) viene dada por:

Se pide:
a Verificar que la población es función continua del tiempo.
b Calcular la tasa de variación media de la población en los intervalos  y
y  .
.
c Calcular la tasa de variación instantánea en  .
.
Debido a unas pésimas condiciones ambientales, una colonia de un millón de bacterias no comienza su reproducción hasta pasados dos meses. La función que representa la población de la colonia al variar el tiempo (expresado en meses) viene dada por:

Se pide:
a Verificar que la población es función continua del tiempo.
El único punto que debemos analizar es en 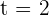 . Notemos que
. Notemos que
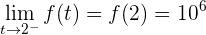 .
.
Además
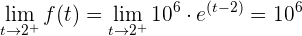 .
.
Por lo tanto es continua.
b Calcular la tasa de variación media de la población en los intervalos  y
y  .
.
Primero hagamos el cálculo para el intervalo 
 .
.
Ahora hagamos el cálculo para el intervalo 
 .
.
c Calcular la tasa de variación instantánea en  .
.
La derivada de 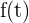 está dada por
está dada por
 ,
,
por lo tanto

3Una población bacteriana tiene un crecimiento dado por la función 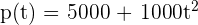 , siendo
, siendo 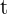 el tiempo metido en horas. Se pide:
el tiempo metido en horas. Se pide:
a La velocidad media de crecimiento.
b La velocidad instantánea de crecimiento.
c La velocidad de crecimiento instantáneo para 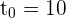 horas.
horas.
Una población bacteriana tiene un crecimiento dado por la función 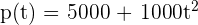 , siendo
, siendo 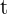 el tiempo metido en horas. Se pide:
el tiempo metido en horas. Se pide:
a La velocidad media de crecimiento.

b La velocidad instantánea de crecimiento.

c La velocidad de crecimiento instantáneo para 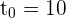 horas.
horas.
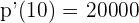
4La ecuación de un movimiento rectilíneo es:  . ¿En qué momento la velocidad en nula? Hallar la aceleración en ese instante.
. ¿En qué momento la velocidad en nula? Hallar la aceleración en ese instante.
La ecuación de movimiento rectilíneo que se nos da es:  . Recordemos que la velocidad es la primer derivada de la función de movimiento, por lo tanto, para encontrar el momento en el cual la velocidad es nula, debemos derivar
. Recordemos que la velocidad es la primer derivada de la función de movimiento, por lo tanto, para encontrar el momento en el cual la velocidad es nula, debemos derivar 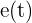 , igualar a cero y despejar
, igualar a cero y despejar 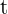 :
:
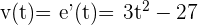 .
.
Igualando a  y despejando
y despejando 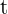

Así, cuando 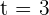 , la velocidad es nula.
, la velocidad es nula.
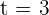 ), debemos derivar
), debemos derivar 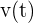 y evaluar en
y evaluar en 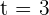 :
: 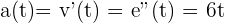 ,
,
evaluando en 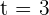 , tenemos
, tenemos
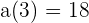 .
.
5La ecuación de un movimiento circular es: 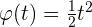 . ¿Cuál es la velocidad y la aceleración angulares al cabo de siete segundos?
. ¿Cuál es la velocidad y la aceleración angulares al cabo de siete segundos?
La ecuación de un movimiento circular es: 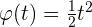 . ¿Cuál es la velocidad y la aceleración angulares al cabo de siete segundos?
. ¿Cuál es la velocidad y la aceleración angulares al cabo de siete segundos?
Tenemos que la velocidad es la primer derivada de la función de movimiento, por lo tanto, para obtener la velocidad a los siete segundos, debemos obtener la derivada de  y evaluar en
y evaluar en  .
.
 .
.
Ahora bien, la aceleración es la segunda derivada de la función de movimiento, por lo tanto, para obtener la aceleración a los siete segundos, debemos obtener la derivada de  y evaluar en
y evaluar en  .
.
 .
.
6Un observador se encuentra a  de lanzamiento de la torre de un cohete. Cuando éste despega verticalmente mide la variación del ángulo
de lanzamiento de la torre de un cohete. Cuando éste despega verticalmente mide la variación del ángulo 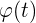 que forma la línea visual que le une con el cohete y la del suelo horizontal en función del tiempo transcurrido. Sabiendo que
que forma la línea visual que le une con el cohete y la del suelo horizontal en función del tiempo transcurrido. Sabiendo que 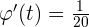 , se pide:
, se pide:
a ¿Cuál es la altura del cohete cuando 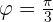 radianes?
radianes?
b ¿Cuál es la velocidad del cohete cuando 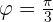 radianes?
radianes?
Un observador se encuentra a  2000 m de lanzamiento de la torre de un cohete. Cuando éste despega verticalmente mide la variación del ángulo
2000 m de lanzamiento de la torre de un cohete. Cuando éste despega verticalmente mide la variación del ángulo 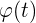 que forma la línea visual que le une con el cohete y la del suelo horizontal en función del tiempo transcurrido. Sabiendo que
que forma la línea visual que le une con el cohete y la del suelo horizontal en función del tiempo transcurrido. Sabiendo que 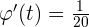 , se pide:
, se pide:
a ¿Cuál es la altura del cohete cuando 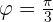 radianes?
radianes?
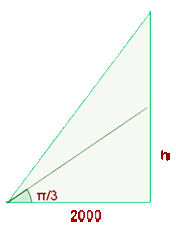

b ¿Cuál es la velocidad del cohete cuando 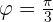 radianes?
radianes?
Debemos calcular la derivada de 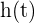 para obtener la velocidad:
para obtener la velocidad:

Por lo tanto
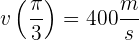
7Se bombea gas a un globo esférico a razón de  . Si la presión se mantiene constante. ¿Cuál es la velocidad con la que cambia el radio del globo cuando el diámetro mide
. Si la presión se mantiene constante. ¿Cuál es la velocidad con la que cambia el radio del globo cuando el diámetro mide 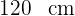 ?
?
Se bombea gas a un globo esférico a razón de  . Si la presión se mantiene constante. ¿Cuál es la velocidad con la que cambia el radio del globo cuando el diámetro mide
. Si la presión se mantiene constante. ¿Cuál es la velocidad con la que cambia el radio del globo cuando el diámetro mide 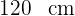 ?
?
De inicio, tenemos que 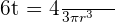 . Entonces, despejando
. Entonces, despejando 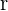 y
y 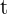 tendríamos
tendríamos

Cuando el diámetro mide 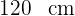 , el radio mide
, el radio mide 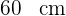 o
o 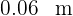 . Evaluando
. Evaluando 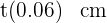 obtenemos el tiempo
obtenemos el tiempo
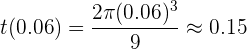
Obteniendo  y evaluando en
y evaluando en 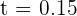 tenemos
tenemos

8¿Cuál es la velocidad que lleva un vehículo se mueve según la ecuación  en el quinto segundo de su recorrido? El espacio se mide en metros y el tiempo en segundos.
en el quinto segundo de su recorrido? El espacio se mide en metros y el tiempo en segundos.
¿Cuál es la velocidad que lleva un vehículo se mueve según la ecuación  en el quinto segundo de su recorrido? El espacio se mide en metros y el tiempo en segundos.
en el quinto segundo de su recorrido? El espacio se mide en metros y el tiempo en segundos.
La velocidad está dada por la derivada,  , entonces para saber la velocidad en el quinto segundo, debemos calcular
, entonces para saber la velocidad en el quinto segundo, debemos calcular 




Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3
4(x+h)-4x/h =4x+4h-4x/h= 4h/h= 4