1 Dada la ecuación 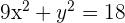 , hallar la ecuación de la recta tangente que sea paralela a la recta de ecuación
, hallar la ecuación de la recta tangente que sea paralela a la recta de ecuación  .
.
 es el punto de tangencia, además conviene saber la pendiente que tiene que tener la recta tangente a la curva. Sabemos que la recta tangente es paralela a la recta
es el punto de tangencia, además conviene saber la pendiente que tiene que tener la recta tangente a la curva. Sabemos que la recta tangente es paralela a la recta 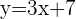 por lo tanto tendrán la misma pendiente.
por lo tanto tendrán la misma pendiente.
Ahora tenemos que encontrar en que punto de la curva dada la pendiente es igual a  , y para ello derivamos implicitamente
, y para ello derivamos implicitamente

entonces
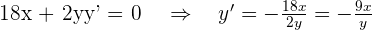
Puesto que la pendiente es tres, entonces

Sustituyendo el punto de tangencia  :
:

y se tiene que cumplir el siguiente sistema

de donde obtenemos que los posibles puntos son

Con estos puntos y la pendiente, obtenemos dos ecuaciones que cumplen con lo que buscamos
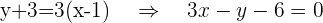
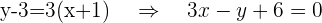
2 Hallar el área del triángulo determinado por los ejes de coordenadas y la tangente a la curva 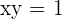 en el punto
en el punto  .
.
Si 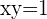 , entonces
, entonces 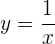
La pendiente de la recta tangente a la curva está dada por la derivada
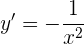
Evaluamos para obtener la pendiente en 
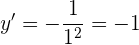
La ordenada del punto se obtiene evaluando en la función original
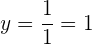
Finalmente
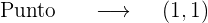
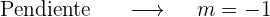
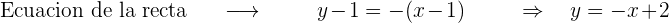
Intersección con el eje OX

Un vértice es 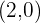
Intersección con el eje OY
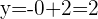
Otro vértice es 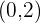
Y la figura es como a continuación
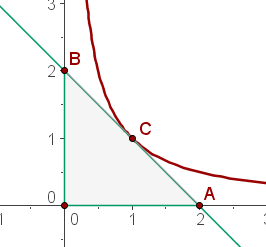
Como es un triángulo rectángulo, su base y altura están dados por los catetos, que en este caso ambos miden  . El área es
. El área es

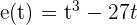 . ¿En qué momento la velocidad en nula? Hallar la aceleración en ese instante.
. ¿En qué momento la velocidad en nula? Hallar la aceleración en ese instante. La ecuación de movimiento rectilíneo que se nos da es:  . Recordemos que la velocidad es la primer derivada de la función de movimiento, por lo tanto, para encontrar el momento en el cual la velocidad es nula, debemos derivar
. Recordemos que la velocidad es la primer derivada de la función de movimiento, por lo tanto, para encontrar el momento en el cual la velocidad es nula, debemos derivar 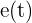 , igualar a cero y despejar
, igualar a cero y despejar 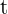 :
:
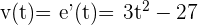 .
.
Igualando a  y despejando
y despejando 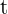

Así, cuando 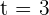 , la velocidad es nula.
, la velocidad es nula.
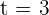 ), debemos derivar
), debemos derivar 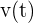 y evaluar en
y evaluar en 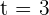 :
: 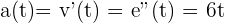 ,
,
evaluando en 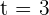 , tenemos
, tenemos
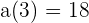 .
.
 árboles por hectárea, cada árbol producirá en promedio
árboles por hectárea, cada árbol producirá en promedio  kilos de nueces cada año. Si por cada árbol adicional que se planta por hectárea la producción promedio por árbol desciende
kilos de nueces cada año. Si por cada árbol adicional que se planta por hectárea la producción promedio por árbol desciende  kilo, ¿cuántos árboles debe plantar para maximizar la producción por hectárea? ¿Cuál es esa producción máxima?
kilo, ¿cuántos árboles debe plantar para maximizar la producción por hectárea? ¿Cuál es esa producción máxima?  : numero de arboles adicionales
: numero de arboles adicionales : Producción por hectárea
: Producción por hectárea
entonces

Derivando  y resolviendo la ecuación que proporciona la primera derivada igual a cero obtenemos los puntos críticos:
y resolviendo la ecuación que proporciona la primera derivada igual a cero obtenemos los puntos críticos:

Luego  proporciona el máximo, con un número de árboles de
proporciona el máximo, con un número de árboles de 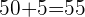 y una producción por hectárea que obtenemos sustituyendo el valor
y una producción por hectárea que obtenemos sustituyendo el valor  en
en  :
:

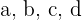 de la función
de la función  para que tenga un vértice en
para que tenga un vértice en 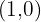 y un punto de inflexión en
y un punto de inflexión en  .
. 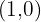 entonces:
entonces: 
Otro dato es que tenemos un punto de inflexión en  , entonces
, entonces

Con lo anterior obtenemos el siguiente sistema de ecuaciones

lo resolvemos y obtenemos
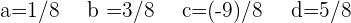
 al número que buscamos. El cual debe ser
al número que buscamos. El cual debe ser  . Para encontrar lo tenemos que minimizar la función:
. Para encontrar lo tenemos que minimizar la función:
entonces


Por tanto, el número buscado es  y el mínimo es
y el mínimo es  .
.
 cm, hallar las dimensiones de aquel cuya área es máxima.
cm, hallar las dimensiones de aquel cuya área es máxima. 
Entonces

Tenemos que maximizar la función:

Derivando

Por lo tanto, los catetos miden  cm cada uno y el área máxima es de
cm cada uno y el área máxima es de 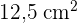 .
.
 pasa por el punto
pasa por el punto 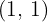 y en ese punto tiene tangente paralela a la recta
y en ese punto tiene tangente paralela a la recta 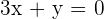 . Hallar
. Hallar  y
y 
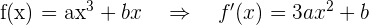
y de la información proporcionada

Resolviendo obtenemos que  y
y  .
.


Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3
4(x+h)-4x/h =4x+4h-4x/h= 4h/h= 4