La pendiente de la recta normal a una curva en un punto es la opuesta de la inversa de la pendiente de la recta tangente, por ser rectas perpendiculares entre sí.
Recordemos que la derivada en un punto 
nos da la pendiente de la recta tangente. Es decir,
Así que la opuesta de la inversa de la derivada de la función, nos da también la pendiente de la recta normal.
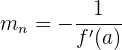
Ecuación de la recta normal
La recta normal a una curva en un punto es aquella que pasa por el punto (a, f(a)) y cuya pendiente es igual a la inversa de la opuesta de f'(a).
Por lo que la ecuación de la recta normal es
Ejemplo de ejercicio de la recta
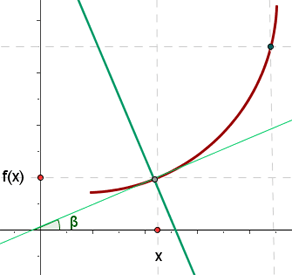
1 Hallar la ecuación de la recta tangente a la parábola y = x² + x + 1 que paralela a la bisectriz del primer cuadrante. Encuentra también la ecuación de la recta normal en dicho punto.
La bisectriz del primer cuadrante tiene de ecuación y = x, por tanto m = 1.
Derivamos la función e igualamos a 1 para calcular el valor de x en el que ocurre esto
Evaluamos x=0 en la función original
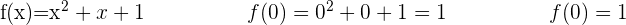
Entonces
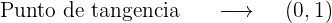
2 Recta normal
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
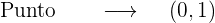
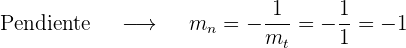
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3
4(x+h)-4x/h =4x+4h-4x/h= 4h/h= 4