1 Estudiar la continuidad y la derivabilidad de la función 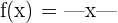 .
.
Estudiar la continuidad y la derivabilidad de la función 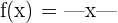 .
.

1En primer lugar estudiamos la continuidad en 

La función es continua.
2Estudiamos la derivabilidad.
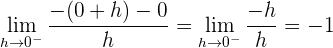
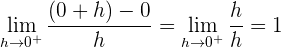
Puesto que las derivadas laterales en  son distintas, la función no es derivable en dicho punto.
son distintas, la función no es derivable en dicho punto.
2 Estudiar la continuidad y la derivabilidad de la función
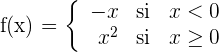
Estudiar la continuidad y la derivabilidad de la función
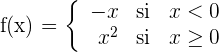
1En primer lugar estudiamos la continuidad en 

La función es continua.
2Estudiamos la derivabilidad.
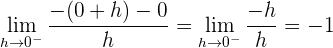
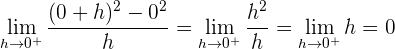
Puesto que las derivadas laterales en  son distintas, la función no es derivable en dicho punto.
son distintas, la función no es derivable en dicho punto.
3 Estudiar la continuidad y la derivabilidad de la función

Estudiar la continuidad y la derivabilidad de la función

1En primer lugar estudiamos la continuidad en 

La función no es continua, por lo tanto tampoco derivable.
4 Estudiar la continuidad y la derivabilidad de la función
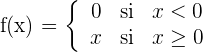
Estudiar la continuidad y la derivabilidad de la función
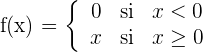
1En primer lugar estudiamos la continuidad en 
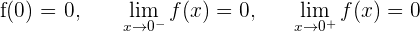
La función es continua.
2Estudiamos la derivabilidad.
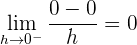
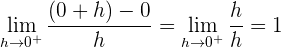
Puesto que las derivadas laterales en  son distintas, la función no es derivable en dicho punto.
son distintas, la función no es derivable en dicho punto.
5Hallar el punto en que 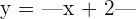 no tiene derivada. Justificar el resultado representando su gráfica.
no tiene derivada. Justificar el resultado representando su gráfica.
Hallar el punto en que 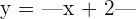 no tiene derivada. Justificar el resultado representando su gráfica.
no tiene derivada. Justificar el resultado representando su gráfica.
1Pasamos a una función a trozos
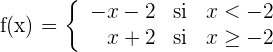
2Estudiamos la continuidad en 
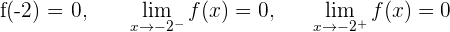
La función es continua en todo  .
.
3Estudiamos la derivabilidad.

Puesto que las derivadas laterales en 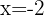 son distintas, la función no es derivable en dicho punto.
son distintas, la función no es derivable en dicho punto.

En 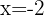 hay un pico, por lo que no es derivable en dicho punto.
hay un pico, por lo que no es derivable en dicho punto.
6Hallar los puntos en que 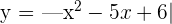 no tiene derivada. Justificar el resultado representando su gráfica.
no tiene derivada. Justificar el resultado representando su gráfica.
Hallar los puntos en que 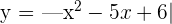 no tiene derivada. Justificar el resultado representando su gráfica.
no tiene derivada. Justificar el resultado representando su gráfica.
1Pasamos a una función a trozos
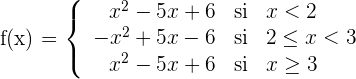
2Estudiamos la continuidad en  y
y 

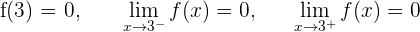
La función es continua en todo  .
.
3Estudiamos la derivabilidad.

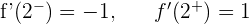
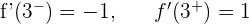
Puesto que las derivadas laterales en  y en
y en  son distintas, la función no es derivable en dichos puntos.
son distintas, la función no es derivable en dichos puntos.
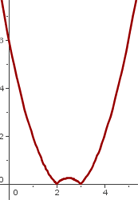
Podemos observar que en x = 2 y en x = 3 tenemos dos puntos angulosos, por lo que la función no será derivable en ellos.
7Estudiar la continuidad y derivabilidad de la función definida por:
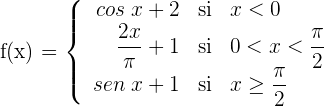
Estudiar la continuidad y derivabilidad de la función definida por:
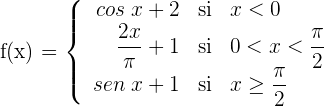
1La función no es continua en  porque no tiene imagen. Por tanto tampoco es derivable.Estudiamos la continuidad en
porque no tiene imagen. Por tanto tampoco es derivable.Estudiamos la continuidad en 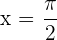
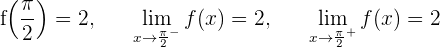
La función es continua en 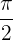 .
.
2Estudiamos la derivabilidad.
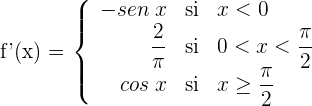
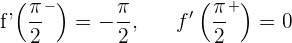
Puesto que las derivadas laterales son distintas, la función no es derivable en 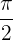 .
.
8Dada la función:
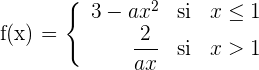
¿Para qué valores de  es derivable?
es derivable?
Dada la función:
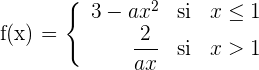
¿Para qué valores de  es derivable?
es derivable?
1Estudiamos la continuidad en 

Para que la función sea continua en  , se requiere que los límites laterales sean iguales
, se requiere que los límites laterales sean iguales

2Estudiamos la derivabilidad en 
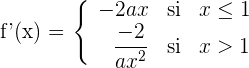
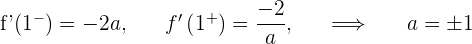
Derivable para 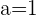 . Para
. Para 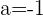 la función no es continua..
la función no es continua..
9Estudiar para qué valores de  y
y  la función es continua y derivable:
la función es continua y derivable:
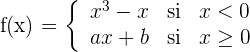
Estudiar para qué valores de  y
y  la función es continua y derivable:
la función es continua y derivable:
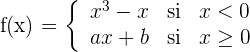
1Estudiamos la continuidad en 

Para que la función sea continua en  , se requiere que los límites laterales sean iguales, entonces
, se requiere que los límites laterales sean iguales, entonces 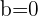
2Estudiamos la derivabilidad en 
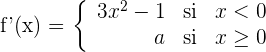
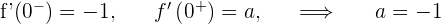
Derivable para 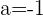 .
.
10Determinar los valores de  y
y  para quien la siguiente función sea derivable en todos sus puntos:
para quien la siguiente función sea derivable en todos sus puntos:
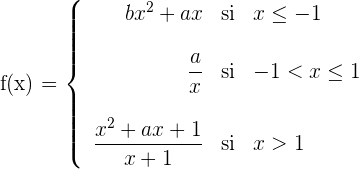
Determinar los valores de  y
y  para quien la siguiente función sea derivable en todos sus puntos:
para quien la siguiente función sea derivable en todos sus puntos:
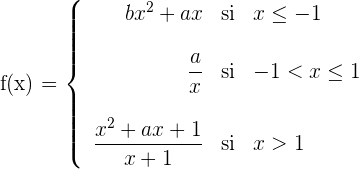
Para qué una función sea derivable en todos sus puntos tiene que ser continua en todos sus puntos. En este caso la función no es continua en  porque no tiene imagen, la función no está definida en ese punto, el resultado de
porque no tiene imagen, la función no está definida en ese punto, el resultado de  no es un número real.
no es un número real.
No existen valores de  y
y  que hagan continua la función.
que hagan continua la función.
Por tanto, no existen valores de  y
y  para los cuales la función sea derivable.
para los cuales la función sea derivable.
11Estudiar para qué valores de  y
y  la función es continua y derivable:
la función es continua y derivable:
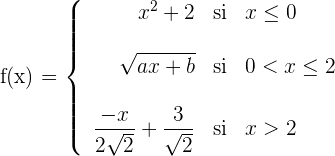
Estudiar para qué valores de  y
y  la función es continua y derivable:
la función es continua y derivable:
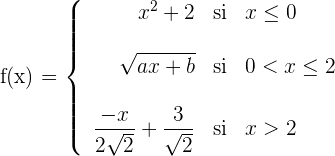
1Estudiamos la continuidad en  y
y 
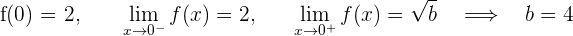
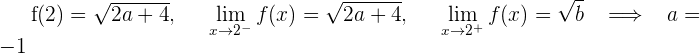
Para que la función sea continua en todo  , se requiere que
, se requiere que 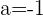 y
y 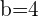
2Estudiamos la derivabilidad en  y
y 

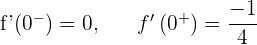
No es derivable en  .
.
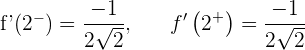
Es derivable en  .
.



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cómo derivo
y=(^5√7x^2+1)/2
Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3