Ejercicios para practicar la definición de continuidad y la de derivada
1 Calcula el valor de la derivada  en
en  .
.
Recordemos que la derivada por definición de  es la siguiente:
es la siguiente:
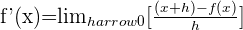
Sustituyendo los valores tenemos la siguiente expresión:

Desarrollamos, sumando la fracción superior:

Cancelamos términos:

Simplificamos la fracción:
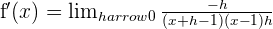

Finalmente calculamos el límite:

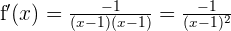
Evaluamos en 
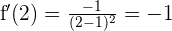
2 Una población bacteriana tiene un crecimiento dado por la función 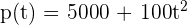 , siendo
, siendo  el tiempo medido en horas. Se pide:
el tiempo medido en horas. Se pide:
a La velocidad media de crecimiento.
b La velocidad instantánea de crecimiento.
c La velocidad de crecimiento instantáneo para 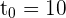 horas.
horas.
aLa velocidad media de crecimiento.
Recordemos que la ecuación para calcular la velocidad media es la siguiente:
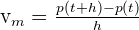
Sustituyendo obtenemos:
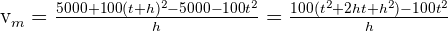
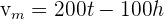
bLa velocidad instantánea de crecimiento.
Recordemos que la velocidad instantánea es la derivada de la función, en este caso necesitamos calcular 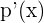 :
:
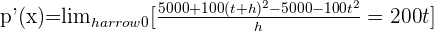
c La velocidad de crecimiento instantáneo para 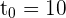 horas.
horas.
Como 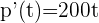 , para calcular la velocidad instantánea sustituimos:
, para calcular la velocidad instantánea sustituimos:
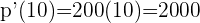
3 Hallar los puntos en que  no tiene derivada.
no tiene derivada.
Primero, transformamos la función en una función a trozos:
Calculamos para que valores de  se satisface que
se satisface que  :
:
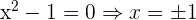
De esta manera, podemos concluir que la función se comporta por intervalos (considerando un valor para cada intervalo y observando el signo de la imagen):

Así, podemos reescribir la función de la siguiente manera:

Estudiamos la continuidad en 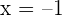 y en
y en 
Para lo anterior, calculamos el valor de  y sus límites por la derecha y la izquierda:
y sus límites por la derecha y la izquierda:

Como los valores coinciden en ambos casos, entonces la función es continua en toda  .
.
Ahora, estudiamos la derivabilidad en 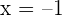 y en
y en  :
:

Calculamos el límite por la izquierda y derecha de  :
:
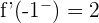

Las derivadas laterales de la función no coinciden por lo cual la función no será derivable en  .
.
Calculamos el límite por la izquierda y derecha de 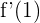 :
:
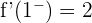
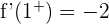
Las derivadas laterales de la función no coinciden por lo cual la función no será derivable en  .
.
4 Estudiar para qué valores de  y
y  la función es continua y derivable:
la función es continua y derivable:


Primero, analicemos la continuidad
En  tenemos:
tenemos:
Calculamos el valor de la imagen en  :
:
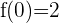
Límite lateral izquierdo:

Límite lateral derecho:
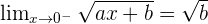
Para que la función sea continua se debe satisfacer:
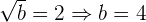
Después, analicemos la continuidad en  :
:
El valor de la imagen de la función es el siguiente:
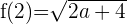
Límite lateral izquierdo:

Límite lateral derecho:

Para que la función sea continua en  se debe satisfacer:
se debe satisfacer:

Así bien, si 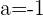 y
y  la función es continua en
la función es continua en 
Después estudiemos la derivabilidad:

En 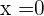
Tenemos que el límite lateral izquierdo de la derivada es  mientras que en que el límite lateral derecho de la derivada es
mientras que en que el límite lateral derecho de la derivada es 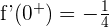 . Por lo cual, la función no es derivable en
. Por lo cual, la función no es derivable en  .
.
En 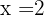 :
:
Tenemos que el límite lateral izquierdo de la derivada es 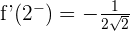 y el límite lateral derecho de la derivada es
y el límite lateral derecho de la derivada es 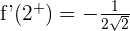 . Como los límites coinciden entonces la función es derivable en
. Como los límites coinciden entonces la función es derivable en  .
.
5Determinar los valores del parámetro  , para qué las tangentes a la curva de la función
, para qué las tangentes a la curva de la función  en los puntos de abscisas
en los puntos de abscisas  ,
,  sean paralelas.
sean paralelas.
Para que sean paralelas se tiene que cumplir que las derivadas en  y
y  sean iguales. Es decir_
sean iguales. Es decir_
 .
.
Calculamos la derivada:
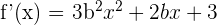
Y después, calculamos el valor de la derivada en 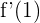 y
y  :
:
 .
.

Sustituimos en la ecuación 1 y tenemos la siguiente igualdad:

Simplificamos y resolvemos:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3
4(x+h)-4x/h =4x+4h-4x/h= 4h/h= 4