Capítulos
Calcular la derivada
1 Calcular las derivadas en los puntos que se indica:
-
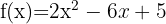en 
. -
en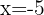 
. -
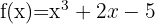en 
. -
en 
.
Recordemos que una manera de calcular la derivada es a través de su definición, esto es, calculando el siguiente límite
1 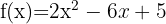en
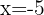
Obtener la derivada
Eliminamos paréntesis desarrollando
Cancelamos términos y factorizamos la 
en el numerador
Simplificamos y calculamos el límite
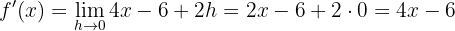
Finalmente
Evaluar
Evaluamos la derivada en el punto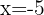
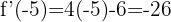
2 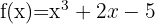en .
Obtener la derivada
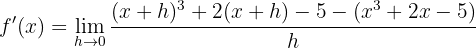
Eliminamos paréntesis desarrollando
Cancelamos términos y factorizamos la en el numerador
Simplificamos y calculamos el límite
Finalmente
Evaluar
Evaluamos la derivada en el punto
3 en
Obtener la derivada
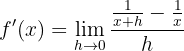
Desarrollamos
Simplificamos y calculamos el límite
Evaluar
Evaluamos la derivada en el punto
4 en .
Obtener la derivada
Mutliplicamos por el conjugado para racionalizar
Desarrollamos
Simplificamos y calculamos el límite
Evaluar
Evaluamos la derivada en el punto
2 ¿Cuál es la velocidad que lleva un vehículo se mueve según la ecuación 
en el quinto segundo de su recorrido? El espacio se mide en metros y el tiempo en segundos.
Obtener la derivada
La velocidad es igual a la derivada de la ecuación de posición, en este caso 
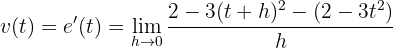
Eliminamos paréntesis desarrollando
Cancelamos términos y factorizamos la en el numerador
Simplificamos y calculamos el límite
Evaluar
Encontrar las coordenadas
3 Dada la curva de ecuación 
, halla las coordenadas de los puntos de dicha curva en los que la tangente forma con el eje OX un ángulo de 45°.
Obtener la derivada
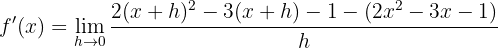
Eliminamos paréntesis desarrollando
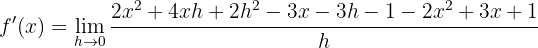
Cancelamos términos y factorizamos la en el numerador
Simplificamos y calculamos el límite
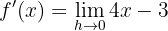
Igualar la derivada y obtener el valor de la abscisa
Queremos que la recta tangente a la curva forme un ángulo de 45° con el eje OX, es decir, queremos que su pendiente tenga de valor 
Esto es,
4x-3=1 \hspace{2cm} 4x=4 \hspace{2cm} x=1
Obtener la ordenada y encontrar el punto
Evaluamos el punto en 
y así obtenemos la ordenada del punto
Estudiar continuidad y derivabilidad
4 Debido a unas pésimas condiciones ambientales, una colonia de un millón de bacterias no comienza su reproducción hasta pasados dos meses. La función que representa la población de la colonia al variar el tiempo (expresado en meses) viene dada por:
Se pide:
-
Verificar que la población es función continua del tiempo.
-
Calcular la tasa de variación media de la población en los intervalos [0, 2] y [0, 4].
-
Calcular la tasa de variación instantánea en t = 4.
1 Continuidad
Una función constante y exponencial son continuas, por lo que claramente 
es continua en 
y 
.
Resta verificar si es continua en el punto
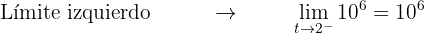
Como estos tres valores son iguales, la función es continua en 2, y con esto, es continua en todos los puntos.
2 Tasa de variación media en [0, 2] y [0, 4]
En [0, 2]
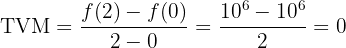
En [0, 4]
3 Tasa de variación instantánea en t = 4
La derivada está dada por la función
La derivada en t=4 es
Se ha hallado la derivada de la función exponencial mediante la fórmula inmediata.
5 Hallar el punto en que 
no tiene derivada. Justificar el resultado representando su gráfica.
La función es equivalente a la siguiente función
La función es claramente continua y derivable para los valores 
y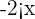 
Sólo queda verificar si lo es en el punto 
Estudiamos la continuidad en 
Podemos verificar que
Y por lo tanto la función es continua en toda 
Por otro lado, la función derivada está dada por
Estudiamos la derivabilidad en
Entonces el límite izquierdo y derecho están dados por
Como no son iguales podemos concluir que no es derivable en: .
Analizamos la gráfica
En hay un pico, por lo que no es derivable en ese punto.
6 Hallar los puntos en que 
no tiene derivada. Justificar el resultado representando su gráfica.
La función es equivalente a la siguiente función
La función es claramente continua y derivable para los valores 
, 
y 
Sólo queda verificar si lo es en los puntos y
Estudiamos la continuidad en 
y en 
Podemos verificar que
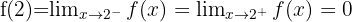
Entonces la función es continua en toda .
Estudiamos la derivabilidad en y
Podemos verificar que los límites laterales en
Y los límites laterales en son
Como no coinciden las derivadas laterales la función no será derivable en: y .
Analizamos la gráfica
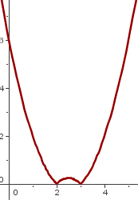
Podemos observar que en y en tenemos dos puntos angulosos, por lo que la función no será derivable en ellos.
7 Estudiar la continuidad y derivabilidad de la función definida por:
La función no es continua en x = 0 porque no tiene imagen. Por tanto tampoco es derivable.
Estudiamos la continuidad en 
El valor en la función es
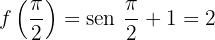
Los límites laterales son
Como estos son iguales la función tiene límite en este punto y además
Por lo tanto es continua en
Veamos si es derivable mediante las fórmulas de derivadas trigonómetricas inmediatas.
Calculamos los límites laterales de la función derivada en
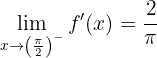
Como las derivadas laterales no coinciden no es derivable en el punto.
Hallar parámetros
8 Dada la función:
¿Para qué valores de a es derivable?
Estudiamos la continuidad en 
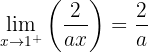
Para que sea continua los límites laterales tienen que ser iguales
Resolvemos la cuadrática
Estudiamos la derivabilidad en
Los límites laterales de la derivada son
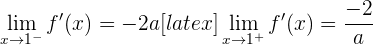
Para que sea derivable los límites laterales tienen que ser iguales
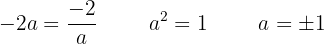
Para ser derivable también tiene que ser continua así que sólo es derivable para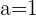 
, pues para 
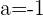no es continua
9 Estudiar para qué valores de a y b la función es continua y derivable:
Estudiamos la continuidad en x = 0
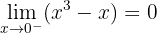
Para que sea continua los límites laterales tienen que ser iguales
Estudiamos la derivabilidad en x = 0
Para que sea derivable los límites laterales tienen que ser iguales
10 Determinar los valores de a y b para que la siguiente función sea derivable en todos sus puntos:
Para qué una función sea derivable en todos sus puntos tiene que ser continua en todos sus puntos. En este caso la función no es continua en x = 0 porque no tiene imagen, la función no está definida en ese punto, el resultado de a/0 no es un número real.
No existen valores de a y b que hagan continua la función.
Por tanto, no existen valores de a y b para los cuales la función sea derivable.
Ejercicios resueltos de cálculo de derivadas
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
me pueden ayudar encontrar la derivada de : y=7 elevado a la 4 + e elevado a la x-4 – ln X + 100
Excelente contenido. Creo es posible mejorar el contenido para que sea más didáctico con más ejemplos, partiendo de lo elemental a lo complejo, para que el texto pueda ser más entendible para estudiantes de secundaria en Costa Rica.
Excelente artículo y muy dinámico.
Agradecemos tu comentario, la verdad estamos trabajando mucho para lograr tener las mejores explicaciones para que sea mas entendible al publico y para ello lo que ustedes recomienden nos ayuda en gran forma, esperamos que en un futuro seamos mejores siguiendo sus sugerencias, otra vez gracias.
Hola: El últipo ejercicio de aplicación me parece que es incorrecto ya que no está obteniendo la derivada del volumen del cono
Hola si te refieres al triángulo que gira, si se derivo el volumen, si estoy equivocado por favor indícamelo.
la pagina mas hermosa que he encontrado bien definida y completa, tendremos algo similar para integrales?
Hola que bueno que te guste la pagina, y si tenemos el tema de integrales tenemos por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/calculo/integrales/ejercicios-resueltos-de-integrales-por-sustitucion.html» esta pagina y otras mas para que las explores.
Está bien la explicación. Pero falta cuando la segunda derivada es igual a cero, que no aplicaría ese criterio.
Hola, que bueno que te gusten las explicaciones, en cuanto a la segunda derivada igualada a cero sirve para encontrar los puntos de inflexión, en cuanto el criterio podrías mencionar su nombre por favor.
Y=X ELEVADA ALA TRES -4X+5