Consideremos una función 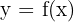 y consideremos dos puntos próximos sobre el eje de abscisas
y consideremos dos puntos próximos sobre el eje de abscisas  y
y 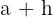 , siendo
, siendo  un número real que corresponde al incremento de
un número real que corresponde al incremento de 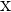 (
( ).
).
Se llama tasa de variación (TV) de la función en el intervalo 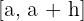 , que se representa por
, que se representa por 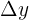 , a la diferencia entre las ordenadas correspondientes a los puntos de las abscisas
, a la diferencia entre las ordenadas correspondientes a los puntos de las abscisas  y
y  .
.



Tasa de variación media
Se llama tasa de variación media (TVM) en intervalo 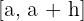 , representada por
, representada por  o
o  , al cociente entre la tasa de variación y la amplitud del intervalo considerado sobre el eje de abscisas,
, al cociente entre la tasa de variación y la amplitud del intervalo considerado sobre el eje de abscisas,  o
o 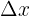 , esto es:
, esto es:
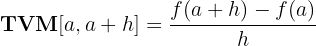
Interpretación geométrica
La expresión anterior coincide con la pendiente de la recta secante a la función 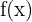 , que pasa por los puntos de abscisas
, que pasa por los puntos de abscisas  y
y  .
.
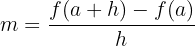
ya que en el triángulo 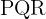 , de la imagen anterior, resulta que:
, de la imagen anterior, resulta que:
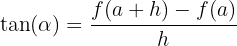
Ejemplos
1. Calcular la TVM de la función 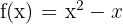 en el intervalo
en el intervalo 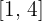 .
.
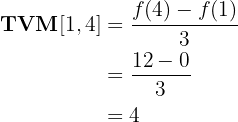
2. El índice de la bolsa de Madrid pasó cierto año de 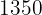 a
a 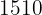 . Hallar la tasa de variación media mensual.
. Hallar la tasa de variación media mensual.














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3
4(x+h)-4x/h =4x+4h-4x/h= 4h/h= 4