Sea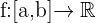 
una función continua en 
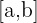con 
entonces existe un punto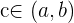 
tal que 
.
Ahora definamos la Propiedad de Darboux,
Propiedad de Darboux
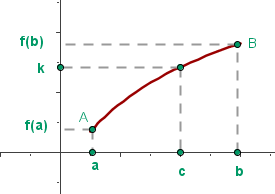
Si una función es continua en el intervalo 
y 
es un número comprendido entre los valores 
y 
, entonces existe algún 
en 
tal que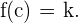 
Podemos decir que la Propiedad de Darboux es una generalización del Teorema de Bolzano, pues al tomar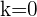 
en el enunciado de la Propiedad de Darboux obtenemos el Teorema de Bolzano.
También podemos definir la propiedad de Darboux de este otro modo:
Si una función es continua en el intervalo la función alcanza en este intervalo todos los valores comprendidos entre y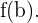 
Ejemplos
1 Probar que la función 
toma el valor 
.
La función es continua en todo 
por ser el producto de dos funciones continuas.
Tomamos el intervalo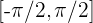 
y estudiamos el valor de las imágenes de los extremos:
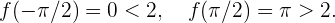
Por tanto existe un 
tal que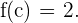 
2 Considere la función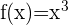 
con dominio 
.
Notemos que
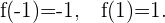
Por lo tanto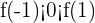 
. De la Propiedad de Darboux o del Teorema de Bolzano tenemos que existe un número 
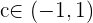tal que . Más aún sabemos que este número es cero.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3