Las hipérbolas son funciones racionales de la forma  , donde
, donde 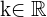 .
.
Por ejemplo, de la función racional  se pueden destacar dos aspectos:
se pueden destacar dos aspectos:
- Sus asíntotas son los ejes
- El centro de la hipérbola, el punto donde se cortan las asíntotas en este caso es el origen.

Además, es posible deducir el comportamiento de otras funciones racionales a partir de la traslación de las hipérbolas como se ilustra en las siguientes secciones.

Traslación vertical
La traslación vertical de una hipérbola consiste en el desplazamiento de una hipérbola centrada en el origen hacia arriba o abajo respecto al origen del plano de coordenadas. De tal manera, que tenemos la siguiente relación:

Donde 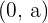 es el centro de la hipérbola, con la particularidad de que:
es el centro de la hipérbola, con la particularidad de que:
- Si
 ,
,  se desplaza hacia arriba
se desplaza hacia arriba  unidades.
unidades. - Si
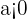 ,
,  se desplaza hacia abajo
se desplaza hacia abajo  unidades.
unidades.
Ejemplo:
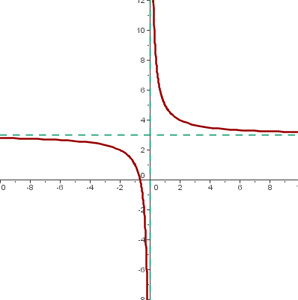
- El centro de la hipérbola es:
 .
. - Como
 ,
,  se desplaza hacia arriba
se desplaza hacia arriba  unidades.
unidades.
Ejemplo:

- El centro de la hipérbola es:
 .
. - Como
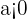 , entonces
, entonces  se desplaza hacia abajo
se desplaza hacia abajo  unidades.
unidades.
Traslación horizontal
La traslación vertical de una hipérbola consiste en el desplazamiento de una hipérbola centrada en el origen hacia la derecha o izquierda respecto al origen del plano de coordenadas. De tal manera, que tenemos la siguiente relación:

Donde 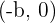 es el centro de la hipérbola, con la particularidad de que:
es el centro de la hipérbola, con la particularidad de que:
- Si
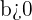 ,
,  se desplaza hacia la izquierda
se desplaza hacia la izquierda  unidades.
unidades. - Si
 ,
,  se desplaza hacia la derecha
se desplaza hacia la derecha  unidades.
unidades.
Ejemplo:

- El centro de la hipérbola es:
 .
. - Como
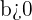 , entonces
, entonces  se desplaza hacia la izquierda
se desplaza hacia la izquierda  unidades.
unidades.
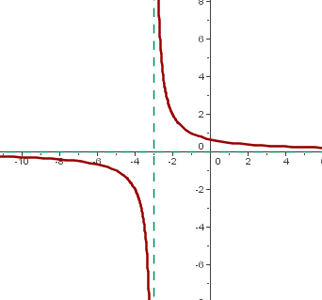
Ejemplo:

- El centro de la hipérbola es:
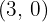 .
. - Como
 , entonces
, entonces  se desplaza hacia la derecha
se desplaza hacia la derecha  unidades.
unidades.
Traslación oblicua
La traslación oblicua de una hipérbola consiste en el desplazamiento de una hipérbola centrada en el origen tanto vertical como horizontalmente, de tal manera, que tenemos la siguiente relación:

Donde  es el centro de la hipérbola, con la particularidad de que:
es el centro de la hipérbola, con la particularidad de que:
- Si
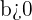 y
y  ,
,  se desplaza hacia la izquierda
se desplaza hacia la izquierda  unidades y hacia arriba
unidades y hacia arriba  unidades.
unidades. - Si
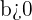 y
y 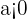 ,
,  se desplaza hacia la izquierda
se desplaza hacia la izquierda  unidades y hacia abajo
unidades y hacia abajo  unidades.
unidades. - Si
 y
y 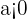 ,
,  se desplaza hacia la derecha
se desplaza hacia la derecha  unidades y hacia abajo
unidades y hacia abajo  unidades.
unidades. - Si
 y
y  ,
,  se desplaza hacia la derecha
se desplaza hacia la derecha  unidades y hacia arriba
unidades y hacia arriba  unidades.
unidades.
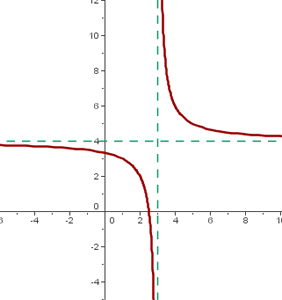
Ejemplo:

- El centro de la hipérbola es:
 .
. - Como
 y
y  , entonces
, entonces  se desplaza hacia la derecha
se desplaza hacia la derecha  unidades y hacia arriba 4 unidades.
unidades y hacia arriba 4 unidades.
Ejemplo:
 .
.
En este caso para resolver necesitamos calcular el resultado de la división, en caso de no recordar el procedimiento puedes consultar la teoría sobre división de polinomios, de tal manera que podemos reescribir la expresión de la siguiente forma:
 .
.- El centro de la hipérbola es:
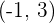 .
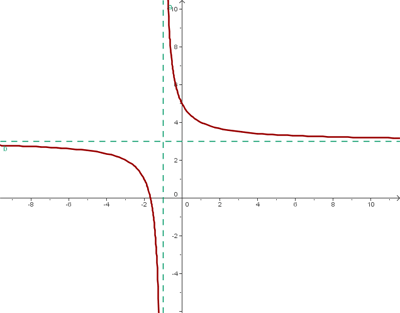
. - Además como
 y
y 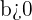 , entonces
, entonces  se desplaza hacia arriba
se desplaza hacia arriba  unidades y hacia la izquierda una unidad.
unidades y hacia la izquierda una unidad.














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3