Temas

Definición de la función inversa
Se llama función inversa o reciproca de  a otra función
a otra función  que cumple que:
que cumple que:
Si  , entonces
, entonces 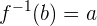
Veamos un ejemplo a partir de la función 
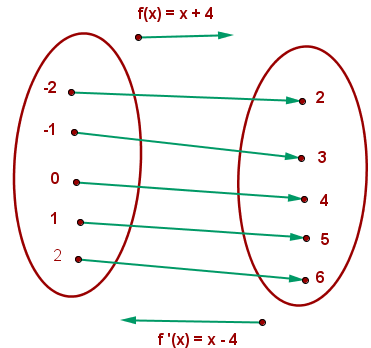
Podemos observar que:
- El dominio de
 es el recorrido de
es el recorrido de  .
. - El recorrido de
 es el dominio de
es el dominio de  .
.
Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.
Si dos funciones son inversas su composición es la función identidad.
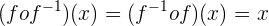
Las gráficas de  y
y  son simétricas respecto de la bisectriz del primer y tercer cuadrante.
son simétricas respecto de la bisectriz del primer y tercer cuadrante.

Hay que distinguir entre la función inversa,  , y la inversa de una función:
, y la inversa de una función: 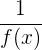 .
.
La inversa de la función  es
es
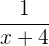 .
.
La función inversa de  es
es  porque la composición de las dos
porque la composición de las dos
funciones es la función identidad

Cálculo de la función inversa
Para construir o calcular la función inversa de una función cualquiera, se deben
seguir los siguientes pasos:
Paso 1: Se escribe la función con  e
e  .
.
Paso 2: Se despeja la variable  en función de la variable
en función de la variable  .
.
Paso 3: Se intercambian las variables.
Ejemplos con ejercicios resueltos
Calcular la función inversa de:
1 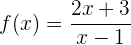
Cambiamos  por
por 

Quitamos denominadores
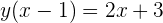
Resolvemos el paréntesis
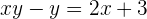
pasamos al primer miembro las 
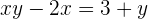
Extraemos el factor común, es decir, la 

Ahora despejamos la 
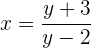
Cambiamos x por  y obtendremos la función inversa
y obtendremos la función inversa
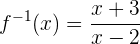
Vamos a comprobar el resultado para 
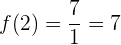
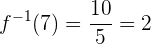
Como  nos resulta
nos resulta  y
y 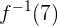 nos resulta
nos resulta 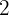 , eso significa que la función inversa es correcta
, eso significa que la función inversa es correcta
2 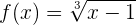
Cambiamos  por
por 
Elevamos al cubo en los dos miembros
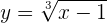

Despejamos la  y cambiamos
y cambiamos  por
por 
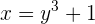

3 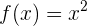
Cambiamos  por
por 
Despejamos la 

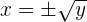
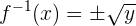
No es una función.
No existe función inversa porque cualquier elemento tiene dos imágenes y una función puede
tener a lo sumo una imagen













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Está mal la solución de la función inversa de f(x) = (2x+3)/x-1
Ya lo revise y no encuentro el error, podrías señalar en que está mal.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Cuántas fórmulas tiene la tabla de valor