
Los/las mejores profesores/as de Matemáticas que están disponibles
Respecto del eje de ordenadas. Función par
Una función f es simétrica respecto del eje de ordenadas cuando para todo x del dominio se verifica:
f(−x) = f(x)
Las funciones simétricas respecto del eje de ordenadas reciben el nombre de funciones pares.
Ejemplo
Comprobar que la siguiente función es par:

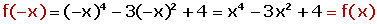

Simetría respecto al origen. Función impar
Una función f es simétrica respecto al origen cuando para todo x del dominio se verifica:
f(−x) = −f(x)
Las funciones simétricas respecto al origen reciben el nombre de funciones impares.
Ejemplo
Comprobar que la siguiente función es impar:
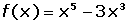














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Está mal la solución de la función inversa de f(x) = (2x+3)/x-1
Ya lo revise y no encuentro el error, podrías señalar en que está mal.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis