Indica si las siguientes relaciones son funciones:
1El coste de comprar fruta y el número de kilos comprados.
2El coste de una llamada telefónica y su duración.
3Velocidad de un vehículo y tiempo empleado en recorrer una distancia.
4Edad de una persona y su color de pelo.
5Color de un diario y número de páginas escritas.
6Cantidad de alumnos de una clase y número de aprobados.
7El sexo de una persona y la cantidad de cigarrillos diarios que fuma.
8Dinero invertido en publicidad por una marca y beneficios obtenidos.
De las funciones a las que se refieren los siguientes enunciados, separa las variables en dependientes e independientes:
9
La electricidad consumida y el importe del recibo a pagar.
La superficie de un cuadrado y la longitud del lado de dicho cuadrado.
La velocidad a la que circula un vehículo y el espacio recorrido.
El importe a pagar y el número de litros repostados en una gasolinera.
Crecimiento del IPC en los doce meses del último año.
El importe del recibo a pagar.
El número de litros repostados en una gasolinera.
Los doce meses del último año.
La electricidad consumida.
El importe a pagar
La superficie de un cuadrado.
La velocidad a la que circula un vehículo.
Crecimiento del IPC.
El espacio recorrido.
La longitud del lado de dicho cuadrado.
| Variable independiente | Variable dependiente |
| La electricidad consumida. | El importe del recibo a pagar. |
| La longitud de su lado. | La superficie de un cuadrado. |
| La velocidad a la que circula. | El espacio recorrido por un vehículo. |
| El número de litros repostados en una gasolinera. | El importe a pagar. |
| Los doce meses del último año. | Crecimiento del IPC. |
Averigua el valor de la variable dependiente en cada caso:
10y = 3x + 1
x = 0 y =
x = 5 y =
x = 0 y = 3 · 0 + 1 = 0 + 1 = 1
x = 5 y = 3 · 5 + 1 = 15 + 1 = 16
11y = 4(2 − x)
x = −3 y =
x = 2 y =
x = −3 y = 4 · [2 − (−3)] = 4 · 5 = 20
x = 2 y = 4 · (2 − 2) = 4 · 0 = 0
12y = (x + 4)²
x = −6 y =
x = 6 y =
x = −5 y = (−6 + 4)² = (−2)² = 4
x = 6 y = (6 + 4)² = 10² = 100
13f(x) = 4x − 7
f(0) =
f(2) =
f(0) = 4 · 0 − 7 = 0 − 7 = −7
f(2) = 4 · 2 − 7 = 8 − 7 = 1
14f(x) = −7x + 8
f(−3) =
f(4) =
f(−3) = −7 · (−3) + 8 = 21 + 8 = 29
f(4) = −7 · 4 + 8 = −28 + 8 = −20
15f(x) = (3x − 2)³
f(0) =
f(3) =
f(0) = (3 · 0 − 2)³ = (−2)³ = −8
f(3) = (3 · 3 − 2)³ = 7³ = 343
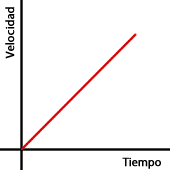
16Arrastra cada gráfica al recipiente que corresponda, sabiendo que la función debe representar la velocidad de llenado del recipiente en cuestión en función del tiempo:








 |  |  |  |  |
 |  |  |  |  |
Debemos tener en cuenta que la velocidad de llenado depende de la anchura del recipiente en cuestión.
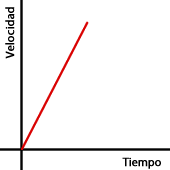
Los vasos con forma de cilindro no tienen zonas con distinto ancho, por lo que sus gráficas se corresponderán con funciones lineales. Para distinguir una de la otra debemos fijarnos en que el más pequeño, al ser más estrecho, se llenará antes, por lo que la velocidad será mayor. Así, la gráfica del vaso con forma de cilindro más estrecho será la más inclinada de las dos candidatas.
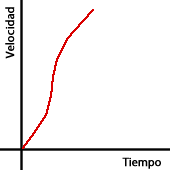
La segunda figura, es decir, el vaso con forma de cono invertido es más esrecho por debajo y más ancho por arriba, por tanto, su gráfica es una curva que muestra que la velocidad de llenado es mayor al principio y menor más adelante.
El vaso con forma de cono es más ancho por debajo y más estrecho por arriba, por tanto, su gráfica es una curva que muestra que la velocidad de llenado es menor al principio y mayor más adelante.
El último recipiente es más ancho por la parte inferior y por la superior, estrechándose en la zona intermedia. Por tanto su gráfica comienza marcando una velocidad de llenado no demasiado rápida, que va aumentando (debido a la zona estrecha) y que vuelve a disminuir (por el ensachamiento de la zona superior del recipiente)
Responde a las preguntas planteadas en cada caso:
18La gráfica muestra la temperatura media de un enfermo en cada uno de los 10 días que ha estado ingresado en el hospital.
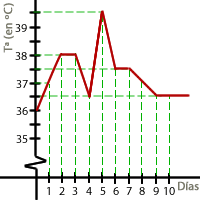
¿Qué día alcanzó la temperatura máxima?
El día
¿Cuál fue esta temperatura?
ºC
¿Entre que dos días se produce la variación máxima de temperatura?
Entre los días y
¿Cuál es esta variación?
ºC
La temperatura máxima se alcanzó el día 5.
Esta temperatura fue de 39.5 ºC.
La variación máxima de temperatura se produce entre el día 4 y el día 5.
Dicha variación es de 3 ºC, en efecto 39.5 − 36.5 = 3 ºC
19Juan sale de casa con el objetivo de hacer un poco de deporte. Empieza caminando a un ritmo normal y después va a diferentes ritmos alternando carrera y paseo.
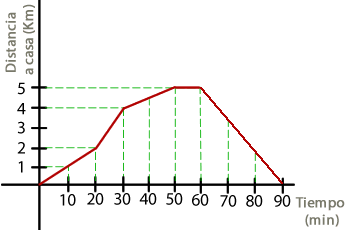
¿Cuánto tiempo pasa fuera de casa?
min
¿Durante cuánto tiempo está en movimiento?
min
¿Qué distancia ha recorrido a la media hora de salir de casa?
Km
¿Se para en algún momento?
¿Cuál es el máximo tiempo que pasa Juan sin descansar?
min
Pasa fuera de casa 90 min.
Está en movimiento durtante 80 min, puesto que tras estar 50 minutos en actividad podemos observar que hace una parada de 10 minutos.
A la media hora de salir de casa ha recorrido 4 Km.
Sí, se para entre el minuto 50 y el 60. Es decir, hace una parada de 10 minutos.
El máximo tiempo que pasa Juan sin desansar son 50 min.
20La gráfica muestra la variación de temperatura durante algunas horas de un día de primavera en Cracovia.
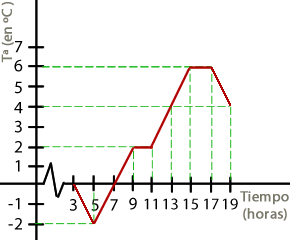
¿De cuántas horas se nos da información en dicha gráfica?
¿Qué temperatura había a las 7 de la mañana?
ºC
¿Qué temperatura había a las 10 de la mañana?
ºC
¿Cuál es la temperatura máxima que se ha alcanzado?
ºC
Se nos da información de 16 horas.
A las 7 de la mañana había una temperatura de 0 ºC.
A las 10 de la mañana había una temperatura de 2 ºC.
La temperatura máxima que se ha alcanzado es de 6 ºC.
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Está mal la solución de la función inversa de f(x) = (2x+3)/x-1
Ya lo revise y no encuentro el error, podrías señalar en que está mal.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Cuántas fórmulas tiene la tabla de valor