Temas
La inferencia estadística estudia los métodos para sacar conclusiones generales de toda una población a partir del análisis de una muestra. Además, estudia el grado de fiabilidad o confianza de los resultados obtenidos. Aquí te damos un resumen de los métodos más comunes que se utilizan en la inferencia estadística.
Tipos de muestreo
El muestreo consiste en tomar un subconjunto de una población. La muestra se suele denotar como 
y la población como 
. Se distinguen los siguientes tipos de muestreo:
Muestreo aleatorio simple
En el muestreo aleatorio se enumeran todos los elementos de la población. Luego, se eligen al azar 
individuos de la población.
1 Si después de escoger al individuo 
, este ya no puede volver escogerse, entonces el muestreo se conoce como sin repetición.
2 Por el otro lado, si el individuo puede ser elegido más de una vez, entonces el muestreo se conoce como con repetición.
Muestreo aleatorio sistemático
En el muestreo sistemático se elige un punto inicial aleatorio . A partir de él se toman los demás elementos en intervalos constantes hasta completar la muestra. Es decir, 
donde es aleatorio.
Muestreo aleatorio estratificado
En el muestreo aleatorio estratificado la población se divide naturalmente en distintas clases o estratos (que deben ser mutuamente excluyentes); luego para cada uno de los estratos se hace un muestreo aleatorio simple.
Si el tamaño de cada sub-población es proporcional al tamaño del estrato respecto a la población, entonces se dice que tenemos muestreo estratificado con asignación proporcional.
Muestreo aleatorio por conglomerados
Aquí, la población también se divide en clases (aunque no necesariamente son excluyentes). Para realizar el muestreo por conglomerados, tomamos un muestra de clases en lugar de individuos.
Por ejemplo, en lugar de considerar todos los alumnos de una universidad, tomamos una muestra de los salones: así, entrevistamos a todos los alumnos de estos salones y el muestreo se simplifica.
Distribución de las medias muestrales
El teorema central del límite nos da información sobre la distribución de la media de una muestra. Es muy importante para la inferencia estadística.
Teorema central del límite
Teorema central del límite. Sea una población con media 
y desviación estándar 
. Si tomamos muestra de tamaño 
, entonces las medidas 
de estas muestras siguen aproximadamente una distribución normal con media y desviación estándar 
. Esto es,
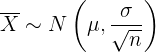
La condición de que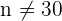 
no es necesaria cuando la población original sigue una distribución normal.
Consecuencias del teorema central del límite
Las siguientes son unas consecuencias importantes del teorema central del límite:
1 Nos permite determinar la probabilidad de que la media de una muestre concreta se encuentre en un intervalo determinado.
2 Permite calcular la probabilidad de que la suma de los elementos de una muestra esté, en principio, en un intervalo dado. Esto debido a que
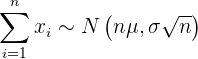
3 Nos ayuda a inferir la media de la población a partir de una muestra.
Estimación de parámetros muestrales
Existen dos maneras para estimar un parámetro o propiedad de una población: estimación puntual y estimación por intervalo.
Estimación puntual
La estimación puntual se hace mediante el cálculo de un sólo número, el cual es la estimación del parámetro. Así, dada una muestra 
, se calcula un número 
el cual se considera como el valor del parámetro poblacional.
Se tienen las siguientes estimaciones puntuales:
1 La media de una población con distribución normal se estima con el promedio
2 La desviación estándar de una población con distribución normal se estima con la desviación muestral
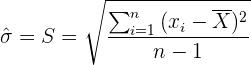
3 La proporción 
de una población con distribución binomial se hace con la la proporción muestral
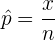
donde 
es el número de elementos en que cumplen con la propiedad deseada.
Esto parece un lío hasta que te lo explican en nuestras clases particulares de matematicas.
Intervalos de confianza
Un intervalo de confianza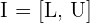 
es un intervalo en donde sabemos que se encuentra el parámetro con un nivel de confianza específico.
El nivel de confianza se refiere a la probabilidad de que el parámetro a estimar se encuentre en nuestro intervalo de confianza. Se suele denotar con 
.
El error de estimación admisible se refiere a la probabilidad que se permite de cometer error. Esta se denota con 
.
El valor crítico de la distribución normal se escribe como 
. El valor crítico satisface que
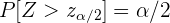
por lo que también se cumple que
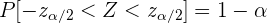
Intervalos característicos
Para la distribución normal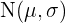 
, los intervalos de confianza tienen la forma
Estos intervalos se conocen también como intervalos característicos.
En la siguiente tabla se encuentran los intervalos característicos para los valores de significación más comunes:
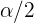|  | | Intervalos característicos |
|---|---|---|---|
| 0.90 | 0.05 | 1.645 |  |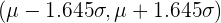
| 0.95 | 0.025 | 1.96 |  |
| 0.99 | 0.005 | 2.575 |  |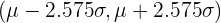
Estimación de la media con intervalo de confianza
Para estimar la media de una población a partir de la muestra , se utiliza el siguiente intervalo de confianza
donde es el promedio de , es la desviación estándar de y es el tamaño de . Además, es el nivel de confianza deseado.
En este caso, el error máximo de estimación es
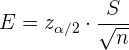
Además, el tamaño de muestra necesario para tener una precisión deseada se calcula mediante
Notemos que para calcular el tamaño de muestra necesario necesitamos conocer la desviación estándar de la población. Esta se puede estimar con una muestra pequeña y luego realizar una segunda muestra con el tamaño de muestra necesario.
Estimación de la proporción con intervalo de confianza
Supongamos que tenemos una población donde una proporción de esta población satisface una característica determinada. Entonces, la proporción de individuos 
que satisface esta propiedad en las muestra de tamaño sigue aproximadamente una distribución normal:
De aquí, se sigue que la estimación de la proporción a partir de la proporción de una muestra se hace mediante el siguiente intervalo:
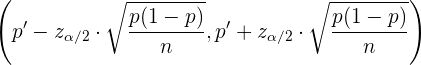
Aquí, el error máximo de estimación está dado por
Hipótesis estadísticas y tipos de contraste
Una prueba estadística (o test estadístico) es un procedimiento para concluir la validez de una hipótesis sobre algún parámetro la población a partir de una muestra.
La hipótesis que se tiene de la población se denota como 
y se llama hipótesis nula. La hipótesis nula siempre debe ser de la forma "es igual a", "es menor o igual" o "es mayor o igual".
La hipótesis contraria a la que se tiene se la población se denota mediante 
y se llama hipótesis alternativa. Esta hipótesis es de la forma "es diferente a", "es mayor a" o "es menor a".
Pasos para realizar una prueba de hipótesis
En general, el procedimiento para realizar una prueba de hipótesis (para la media o la proporción ) es el siguiente:
1 Se hacen enuncian la hipótesis nula y la hipótesis alternativa 
.
2 Determinar el nivel de confianza o de significación .
3 Con esto se calcula el valor (para contraste bilateral) o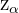 
(para contraste unilateral).
4 Luego, se construye la zona de aceptación del parámetro muestral (mayor detalle en la siguiente sección).
5 Se extrae una muestra de la población con 
para poder utilizar la distribución normal.
6 Se calcula o a partir de la muestra.
7 Si el valor del parámetro muestral está dentro de la zona de aceptación, entonces se acepta la hipótesis nula con un nivel de significación . En caso contrario, se rechaza .
Tipos de contrastes de hipótesis
Supongamos que tenemos una población con un parámetro 
desconocido (que puede ser la media, proporción o desviación estándar). Entonces los contrastes se clasifican como bilateral o unilateral. Estos contrastes se resumen en la siguiente tabla:
| Bilateral |  |  |
|---|---|---|
| Unilateral |  |  |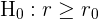
 |  |
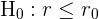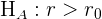Contraste bilateral
El contraste bilateral se da cuando la hipótesis nula es de la forma . En este caso, la hipótesis alternativa tiene la forma .
Para los contrastes bilaterales, el nivel de significación se concentra en dos colas respecto a la media. Si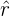 
es el valor del parámetro en la muestra, esto significa que la hipótesis nula se rechaza si 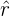es muy grande (cola superior) o muy pequeño (cola inferior) en comparación con .
Para el caso en el que deseamos probar la media de la población, el intervalo de confianza se construye de la siguiente manera:
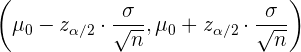
mientras que para el caso de la proporción , el intervalo de confianza es
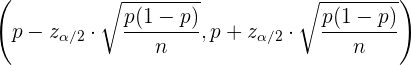
Contraste unilateral
En el contraste unilateral tenemos dos casos. El primer caso es cuando la hipótesis nula es del tipo
por lo que la hipótesis alternativa es del tipo
En este caso, la región de aceptación cuando estamos haciendo una prueba para la media es
mientras que la región de aceptación para la proporción es
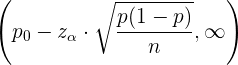
El segundo caso es cuando la hipótesis nula es del tipo
por lo que la hipótesis alternativa es del tipo
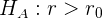
recordemos que puede ser o .
Así, la región de aceptación cuando estamos haciendo una prueba para la media es
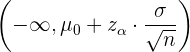
mientras que la región de aceptación para la proporción es
Por último, notemos que en las hipótesis unilaterales tenemos los siguientes valores críticos más comunes:
| | |
|---|---|---|
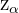| 0.90 | 0.10 | 1.28 |
| 0.95 | 0.05 | 1.645 |
| 0.99 | 0.01 | 2.33 |
Tipos de error
Cuando realizamos pruebas de hipótesis, siempre existe la posibilidad de cometer errores. Los errores se clasifican como error de tipo I y error de tipo II.
El error de tipo I ocurre cuando rechazamos la hipótesis nula siendo verdadera.
El error de tipo II, en cambio, sucede cuando aceptamos la hipótesis nula y esta es verdadera.
Los tipos de error se resumen en la siguiente tabla:
| Verdadera | Falsa |
|---|---|---|
| Aceptar | Decisión correcta Probabilidad de | Decisión incorrecta: Error tipo II |
| Rechazar | Decisión incorrecta Error tipo I Probabilidad de | Decisión correcta |
La probabilidad de cometer el error de tipo I se el nivel de significación .
Por otro lado, la probabilidad de cometer el error de tipo II se suele denotar con 
. En este caso,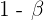 
se conoce como potencia de la prueba. La mejor manera de reducir es aumentando el tamaño de muestra tanto como sea posible.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En la siguiente tabla se presentan las cantidades promedio de jugo de frutas que empacan, en bolsas de litro, tres máquinas empacadas de una agroindustria.
-MAQUINAS
A
B
C
-PROMEDIO EMPACADO POR BOLSA
1.039 LTS
0.989 LTS
1.090 LTS
-DESVIACIÓN ESTANDAR
0.332 LTS
0.350 LTS
0.371 LTS
¿Cuál de las 3 máquinas tiene la cantidad promedio de empacado por bolsa más confiable? ¿Por qué?
ejercicio. En una ciudad de 100.000 habitantes, se quiere estimar la proporción de personas que utilizan bicicleta como medio de transporte. ¿Cuántas personas deben incluirse en la muestra para obtener un margen de error del 5% con un nivel de confianza del 95%?
10.- Las estaturas de cierta población se distribuyen N(168,8). Calcula la probabilidad de que en una muestra de 36 personas la altura media no difiera de la de la población en más de 1 cm.
28 28 28 28 24 24 20 20 20 20 20 25 25 25 27 27 27 26 22 22 22
En una escuela de 150 estudiantes se requiere realizar una investigación sobre las preferencias de las áreas de los estudiantes y se debe calcular su muestra para conocer cuántos estudiantes se le debe aplicar la encuesta, determinando que el grado de confianza es del 95%, la probabilidad de éxito de 98% y el error de calculo del 6%.
Caso de estudio: En el Perú, el Ministerio de Salud (MINSA) está interesado en conocer la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. Para ello, el MINSA decide realizar una encuesta a una muestra de adolescentes de esta población.
Objetivo:
El objetivo del caso de estudio es que los estudiantes apliquen la fórmula para estimar una proporción poblacional para estimar la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. También, debe indicar el tipo de muestreo probabilístico que deberá emplear.
¿Cuál debe ser el tamaño de muestra para estimar la prevalencia de la depresión, con un nivel de confianza del 95%, margen de error de 4%, e indica el método de selección de la muestra
La experiencia con los trabajado indica que el tiempo requerido para que un trabajador cualquiera termine un trabajo, es una variable con distribución aproximada a la normal con una media de 145 minutos y una desviación estándar de 12 minutos. Se lleva a cabo un programa de capacitación con el propósito de mejorar la destreza de los trabajadores y disminuir así el tiempo medio. Para verificar los resultados de dicho programa se toma al azar una muestra de 16 trabajadores y si esta muestra arroja un tiempo medio mayor que 139 minutos se aceptará la hipótesis de que el tiempo medio sigue siendo de 145 minutos. Pruebe la hipótesis con un nivel de significancia del 5%.
Una empresa de seguros ha estado aplicando diferentes técnicas para incrementar sus ventas durante los últi mos 6 meses. El promedio de ventas por semestre es de 54 ventas diarias, con una muestra aleatoria de 60 días de los últimos 6 meses, se obtiene que en promedio hay 60 ventas diarias con una desviación estándar de 28 Con un nivel de significación de 5%, es posible asegu rar que el promedio de ventas aumento?
A una muestra aleatoria de 150 alumnos de la universidad, se le preguntó si había estudiado el idioma inglés. 75 respondieron Sí, 55 respondieron No y 20 no opinaron. a. ¿Cuál es el valor de la estimación puntual de la proporción de la población que responde Sí?. b. ¿Cuál es el valor de la estimación puntual de la proporción de la población que respondió No?. c. Encuentre el intervalo de confianza del 90% para la proporción poblacional que respondieron Sí. Fuente de ingresos Frecuencia Propina sólo domingos 149 Quehaceres, dádivas y domingos 219 Quehaceres y dádivas, no domingos 251 Nada 165 T o t a l 784
Se quiere hacer un estudio para conocer el número de mujeres casadas que van a consulta ginecológicas en una población, por estudios anteriores se sabe que la desviación estándar de 1 mujeres, el investigador considera que el margen de error es de 9% y el coeficiente de confianza es de 91%.