Temas
Bienvenidos a esta serie de ejercicios de inferencia estadística. La inferencia estadística es una herramienta fundamental en el análisis de datos, que nos permite sacar conclusiones y tomar decisiones sobre poblaciones o fenómenos en base a muestras limitadas de información. A través de estos ejercicios, exploraremos cómo utilizar métodos estadísticos para hacer estimaciones, tomar decisiones y evaluar la confiabilidad de nuestros resultados.
Durante esta serie de ejercicios, trabajaremos con conceptos clave como intervalos de confianza, pruebas de hipótesis y análisis de significancia, que nos permitirán sacar conclusiones respaldadas por la evidencia de nuestros datos. A medida que avancemos, aprenderemos a interpretar los resultados obtenidos y a comunicar de manera efectiva las conclusiones que derivamos de ellos.

Muestreo
1 En una fábrica que consta de 600 trabajadores queremos tomar una muestra de 20. Sabemos que hay 200 trabajadores en la sección A, 150 en la B, 150 en la C y 100 en la D.
Si se decide utilizar un muestreo estratificado con asignación proporcional, ¿qué tamaño tendrá cada estrato?
Denotemos como  al tamaño de la población y
al tamaño de la población y  al tamaño de la muestra. Similarmente, denotamos como
al tamaño de la muestra. Similarmente, denotamos como 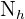 al tamaño del estrato
al tamaño del estrato  y
y  al tamaño de muestra que tomamos de
al tamaño de muestra que tomamos de  . De este modo, cuando tenemos asignación proporcional, se cumple
. De este modo, cuando tenemos asignación proporcional, se cumple
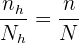
El problema se trata únicamente de encontrar los valores  para cada estrato. Observemos que ya conocemos el tamaño de la población
para cada estrato. Observemos que ya conocemos el tamaño de la población 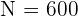 ; los tamaños de cada estrato
; los tamaños de cada estrato 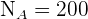 ,
, 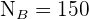 ,
, 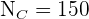 y
y 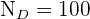 .
.
Además, sabemos que  , por lo que ya tenemos todos los datos para calcular el tamaño de muestra para cada estrato. Primero despejamos
, por lo que ya tenemos todos los datos para calcular el tamaño de muestra para cada estrato. Primero despejamos  :
:
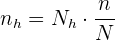
Así, para la sección A debemos tomar:

Para la sección B:
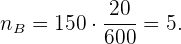
Para la sección C:
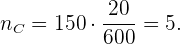
Por último, para la sección D:

Por último, verificamos que

2 En cierta cadena de centros comerciales trabajan 150 personas en el departamento de personal, 450 en el departamento de ventas, 200 en el departamento de contabilidad y 100 en el departamento de atención al cliente. Con objeto de realizar una encuesta laboral, se quiere seleccionar una muestra de 180 trabajadores.
a ¿Qué tipo de muestreo deberíamos utilizar para la selección de la muestra si queremos que incluya a trabajadores de los cuatro departamentos mencionados?
b ¿Qué número de trabajadores tendríamos que seleccionar en cada departamento si utilizamos asignación proporcional?
a El muestreo estratificado (con o sin asignación proporcional) es el único que nos garantiza que tomaríamos trabajadores de los cuatro departamentos.
b El procedimiento es similar al de los ejercicios anteriores. Primero, el tamaño de la población es
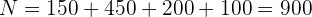
y el tamaño de muestra es 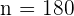 . Así, el número de trabajadores del departamento de personal que debemos escoger es
. Así, el número de trabajadores del departamento de personal que debemos escoger es
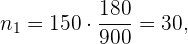
el número del departamento de ventas es
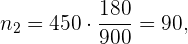
el número del departamento de contabilidad es

y el número de trabajadores que debemos tomar del departamento de atención al cliente es

3 En cierta institución educativa se tienen 100 docentes, 95 administrativos y 505 alumnos. Se realiza muestra de 30 personas. ¿Qué número de personas tendríamos que seleccionar en cada grupo si utilizamos asignación proporcional?
El tamaño de la población es
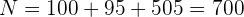
y el tamaño de muestra es 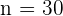 . Así, el número de personas del grupo de docentes que debemos escoger es
. Así, el número de personas del grupo de docentes que debemos escoger es

el número de administrativos es
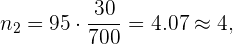
el número de alumnos es
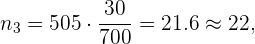
Probabilidad de las muestras
Si estás buscando un profesor de algebra lineal seguro que encuentras al tuyo en Superprof.
4 Considera la siguiente población:  .
.
a Escriba todas las muestras posibles de tamaño dos, escogidas mediante muestreo aleatorio simple y sin reemplazo.
b Calcule la varianza de la población.
c Calcula la varianza de las medias muestrales de las muestras de tamaño dos.
a Las posible muestras son todos los posibles subconjuntos de la población. Es decir,

b Para calcular la varianza necesitamos calcular primero la media de la población, que es

Así, la varianza es

c Recordemos que las medias posibles pueden verse como otra población. Debido a que las posibles muestras son  y
y  , entonces tenemos tres posibles medias muestrales:
, entonces tenemos tres posibles medias muestrales:
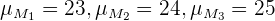
es decir, la población de medias muestrales (para muestras de tamaño dos) es

Debemos calcular la varianza de  . Para ello, primero calculamos su media:
. Para ello, primero calculamos su media:

Por lo que la varianza es

Observemos que la varianza de las medias es menor que la varianza de la población original.
5 Considera la siguiente población:  .
.
a Escriba todas las muestras posibles de tamaño dos, escogidas mediante muestreo aleatorio simple y con reemplazo.
b Calcule la varianza de la población.
c Calcula la varianza de las medias muestrales de las muestras de tamaño dos.
a Las posible muestras son todos los posibles subconjuntos de la población. Es decir,
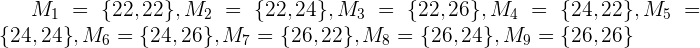
b Para calcular la varianza necesitamos calcular primero la media de la población, que es

Así, la varianza es

c Recordemos que las medias posibles pueden verse como otra población. Debido a que las posibles muestras son 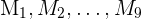 , entonces tenemos nueve posibles medias muestrales:
, entonces tenemos nueve posibles medias muestrales:
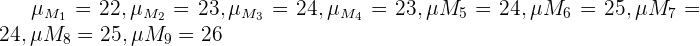
es decir, la población de medias muestrales (para muestras de tamaño dos) es
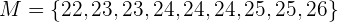
Debemos calcular la varianza de  . Para ello, primero calculamos su media:
. Para ello, primero calculamos su media:
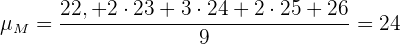
Por lo que la varianza es

Observemos que la varianza de las medias es menor que la varianza de la población original.
6 La variable altura de las alumnas que estudian en una escuela de idiomas sigue una distribución normal de media 1,62 m y la desviación típica 0,12 m. ¿Cuál es la probabilidad de que la media de una muestra aleatoria de 100 alumnas sea mayor que 1.60 m?
Este ejercicio se resuelve similar al problema anterior. Tenemos una variable aleatoria  que sigue una distribución normal, es decir,
que sigue una distribución normal, es decir,
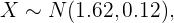
entonces el promedio sigue también una distribución normal
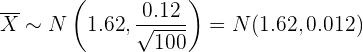
Así, la probabilidad se calcula utilizando

En este caso, si utilizamos una tabla de distribución normal, el resultado sería

mientras que si utilizamos un programa de computadora, el resultado que nos da es
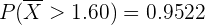
De nuevo, el resultado con programas de computadoras siempre es más preciso. Sin embargo, no importa el método que utilices, el resultado siempre es bastante cercano al real (notemos que los resultados son iguales en 2 cifras después del punto decimal).
7 Las bolsas de sal envasadas por una máquina tienen un peso promedio de  con una desviación estándar de
con una desviación estándar de 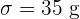 . Las bolsas se empaquetaron en cajas de 100 unidades.
. Las bolsas se empaquetaron en cajas de 100 unidades.
a Calcular la probabilidad de que la media de los pesos de las bolsas de un paquete sea menor que 495 g.
b Calcular la probabilidad de que una caja de 100 bolsas pese más de 51 kg.
a Para responder la primera pregunta, debemos recordar que el promedio de una muestra de tamaño  sigue aproximadamente una distribución normal (debido al teorema central del límite), es decir,
sigue aproximadamente una distribución normal (debido al teorema central del límite), es decir,
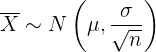
Por tanto, el promedio de las bolsas en cada caja seguirá una distribución
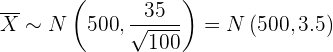
Así, para calcular la probabilidad utilizamos
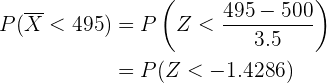
donde  es una variable aleatoria con distribución normal estándar.
es una variable aleatoria con distribución normal estándar.
Esta probabilidad se puede calcular de varias maneras, por ejemplo, utilizar Excel o un lenguaje de programación como R.
Otra forma de calcular esta probabilidad, es utilizando una tabla de probabilidades de la distribución normal, para ello necesitamos escribir la probabilidad de la siguiente manera:

y ya podemos buscar 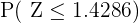 en una tabla distribución normal, donde tenemos que
en una tabla distribución normal, donde tenemos que 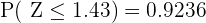 (es el valor más cercano, pues sólo tiene precisión de 2 cifras). Así,
(es el valor más cercano, pues sólo tiene precisión de 2 cifras). Así,
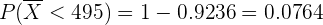
Si utilizamos un lenguaje de programación, el resultado es
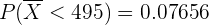
que es bastante similar.
b Este inciso es similar al anterior. La única diferencia es que ahora la variable aleatoria es la suma de los 100 elementos de la muestra. En este caso, por el teorema central del límite, tenemos
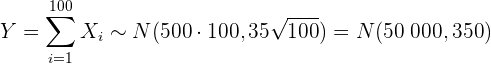
donde  es el peso de la caja en gramos. De este modo, la probabilidad que buscamos es
es el peso de la caja en gramos. De este modo, la probabilidad que buscamos es 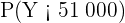 , pues 51 kg es igual a 51 000 g.
, pues 51 kg es igual a 51 000 g.
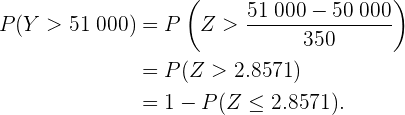
Así, si utilizamos una tabla de distribución normal, el resultado es
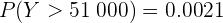
mientras que si utilizamos una Excel o un lenguaje de programación, el resultado da

Recordemos que el resultado obtenido con computadora es más preciso.
Pruebas de hipótesis con estadístico de prueba
Si quieres un profesor en linea algebra ¡encuéntralo en Superprof!
8 En una fábrica de componentes electrónicos, la proporción de componentes finales defectuosos era del 20%. Tras una serie de operaciones e inversiones destinadas a mejorar el rendimiento se analizó una muestra aleatoria de 500 componentes, encontrándose que 90 de ellos eran defectuosos. ¿Qué nivel de confianza debe adoptarse para aceptar que el rendimiento no ha sufrido variaciones?
Para determinar el nivel de confianza, primero debemos observar que se trata de una prueba de hipótesis sobre comparación de proporciones.
Así, la hipótesis nula es (donde 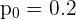 )
)
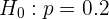
mientras que la hipótesis alternativa es
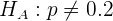
Al realizar el muestreo, obtuvimos que  ,
,  y
y
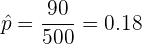
En este caso, el estadístico de prueba es
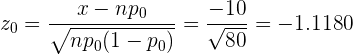
donde 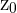 sigue una distribución normal estándar. De este modo, para aceptar la hipótesis nula (esto es, aceptar que no ha habido variación en el rendimiento), basta con que
sigue una distribución normal estándar. De este modo, para aceptar la hipótesis nula (esto es, aceptar que no ha habido variación en el rendimiento), basta con que  donde
donde  es el nivel de confianza.
es el nivel de confianza.
Así, es suficiente con tomar 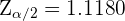 para aceptar la hipótesis nula. Luego,
para aceptar la hipótesis nula. Luego,
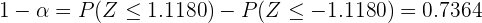
Esto quiere decir que si tomamos un nivel de confianza tan bajo como 73.64%, ya es suficiente para aceptar que el rendimiento no ha sufrido variaciones. Aunque la confianza puede ser del 80% o hasta el 99%.
Recordemos que aceptar la hipótesis nula, simplemente estamos diciendo que no hay evidencia suficiente para rechazarla.
Nota: Otra forma de probar la hipótesis es crear un intervalo de confianza a partir de 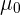 . Al ser la hipótesis bilateral, entonces el intervalo de confianza se calcula utilizando
. Al ser la hipótesis bilateral, entonces el intervalo de confianza se calcula utilizando
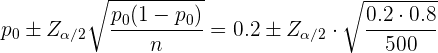
modo que el intervalo de confianza es
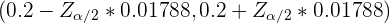
para aceptar la hipótesis, se suficiente con que
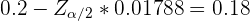
que al despejar  obtenemos
obtenemos
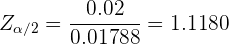
que era justo lo que habíamos obtenido antes. De aquí se sigue que la confianza es de 73.64%.
9 Un sociólogo ha pronosticado, que en una determinada ciudad, el nivel de abstención en las próximas elecciones será del 40% como mínimo. Se elige al azar una muestra aleatoria de 200 individuos, con derecho a voto, 75 de los cuales estarían dispuestos a votar. Determinar con un nivel de significación del 1%, si se puede admitir el pronóstico.
En este caso, se trata de una prueba de hipótesis para la proporción. Sin embargo, ahora se trata de un contraste unilateral, pues hipótesis nula es
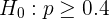
mientras que la hipótesis alternativa es

donde  es la proporción de los individuos que se abstendrán en las próximas elecciones y
es la proporción de los individuos que se abstendrán en las próximas elecciones y 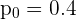 es la proporción hipotética.
es la proporción hipotética.
Así, el estadístico de prueba es

donde 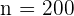 ,
, 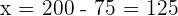 . Con esto, el estadístico toma el valor de
. Con esto, el estadístico toma el valor de
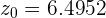
Luego, debido a que se trata de un contraste unilateral, la hipótesis se rechaza si  . Luego, a
. Luego, a 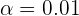 le corresponde el valor crítico
le corresponde el valor crítico  . Así, como
. Así, como

entonces aceptamos  .
.
Por tanto, podemos afirmar, con un nivel de significancia del 1% que la abstención será como mínimo del 40%.
Nota: si creamos un intervalo de confianza alrededor de 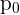 (unilateral), el límite inferior sería
(unilateral), el límite inferior sería

que, al sustituir, obtenemos
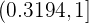
y como  está en el intervalo de confianza, entonces aceptamos la hipótesis nula. Esta es una forma equivalente de realizar la prueba de hipótesis.
está en el intervalo de confianza, entonces aceptamos la hipótesis nula. Esta es una forma equivalente de realizar la prueba de hipótesis.
10 Un informe indica que el precio medio del billete de avión entre Canarias y Madrid es, como máximo, de 120 € con una desviación típica de 40 €. Se toma una muestra de 100 viajeros y se obtiene que la media de los precios de sus billetes es de 128 €.
¿Se puede aceptar, con un nivel de significación igual a 0,1, la afirmación de partida?
En esta prueba de hipótesis estamos probando si la media es menor o igual a cierto valor. Por tanto, la hipótesis nula es
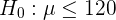
y la hipótesis alternativa es
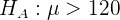
donde 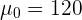 es el valor hipotético. Al realizar el muestreo, obtuvimos
es el valor hipotético. Al realizar el muestreo, obtuvimos  ,
, 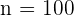 y
y 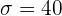 . Por tanto, nuestro estadístico de prueba es
. Por tanto, nuestro estadístico de prueba es

que toma el valor de 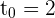 .
.
Como se trata de un contraste unilateral, el criterio de rechazo de la hipótesis nula es  . En este caso, a
. En este caso, a 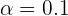 le corresponde un valor crítico de
le corresponde un valor crítico de 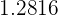 .
.
Luego, como
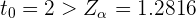
entonces rechazamos la hipótesis nula.
De este modo, concluimos que la media de los precios de los boletos de avión no es de 120 € como máximo. Tenemos evidencia para confirmar que la media es mayor a 120 euros.
11 Un agrónomo informa que la producción media de las plantas de jitomate es, como mínimo, de 5 kg con una desviación típica de 1.3 kg. Se toma una muestra de 90 plantas y se obtiene que la media de de la producción por planta es de 4.5 kg.
¿Se puede aceptar, con un nivel de significación igual a 0,1, la afirmación de partida?
En esta prueba de hipótesis estamos probando si la media es mayor o igual a cierto valor. Por tanto, la hipótesis nula es
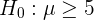
y la hipótesis alternativa es

donde 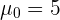 es el valor hipotético. Al realizar el muestreo, obtuvimos
es el valor hipotético. Al realizar el muestreo, obtuvimos 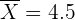 ,
, 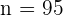 y
y 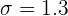 . Por tanto, nuestro estadístico de prueba es
. Por tanto, nuestro estadístico de prueba es

que toma el valor de  .
.
Como se trata de un contraste unilateral, el criterio de rechazo de la hipótesis nula es  . En este caso, a
. En este caso, a 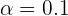 le corresponde un valor crítico de
le corresponde un valor crítico de  .
.
Luego, como

entonces rechazamos la hipótesis nula.
De este modo, concluimos que la media de los kilogramos producidos por las plantas de jitomate no es de 5 kg como mínimo. Tenemos evidencia para confirmar que la media es menor a 5 kilogramos.
Pruebas de hipótesis con intervalos de confianza
12 Un fabricante de lámparas eléctricas está ensayando un nuevo método de producción que se considerará aceptable si las lámparas obtenidas por este método dan lugar a una población normal de duración media 2400 horas, con una desviación típica igual a 300. Se toma una muestra de 100 lámparas producidas por este método y esta muestra tiene una duración media de 2320 horas. ¿Se puede aceptar la hipótesis de validez del nuevo proceso de fabricación con un riesgo igual o menor al 5%?
En este caso se trata de una prueba de hipótesis donde queremos verificar que la media sea igual a cierto valor. Por tanto, la hipótesis nula es
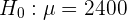
y la hipótesis alternativa es
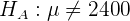
donde 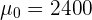 es el valor hipotético.
es el valor hipotético.
Como estamos probando la media de la población, entonces el intervalo de confianza se construye mediante
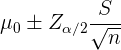
ya que el contraste es bilateral. Así, en el muestreo obtuvimos que 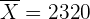 ,
, 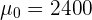 ,
,  y
y 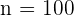 . Luego, a la significancia de
. Luego, a la significancia de  le corresponde un valor crítico de
le corresponde un valor crítico de 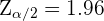 . Así, se tiene que el intervalo de confianza es
. Así, se tiene que el intervalo de confianza es
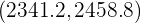
y como 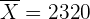 se encuentra fuera del intervalo de confianza, entonces rechazamos la hipótesis nula.
se encuentra fuera del intervalo de confianza, entonces rechazamos la hipótesis nula.
En consecuencia, concluimos que el nuevo proceso de fabricación no es aceptable.
13 El control de calidad una fábrica de pilas y baterías sospecha que hubo defectos en la producción de un modelo de batería para teléfonos móviles, bajando su tiempo de duración. Hasta ahora el tiempo de duración en conversación seguía una distribución normal con media 300 minutos y desviación típica 30 minutos. Sin embargo, en la inspección del último lote producido, antes de enviarlo al mercado, se obtuvo que de una muestra de 60 baterías el tiempo medio de duración en conversación fue de 290 minutos. Suponiendo que ese tiempo sigue siendo Normal con la misma desviación típica:
¿Se puede concluir que las sospechas del control de calidad son ciertas a un nivel de significación del 2%?
Como suponemos que el tiempo de vida se redujo, entonces se trata de una prueba de hipótesis donde queremos verificar que la media es menor a cierto valor. Así, la hipótesis nula es
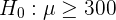
y la hipótesis alternativa es

donde  es la media hipotética.
es la media hipotética.
El intervalo de confianza para la media es
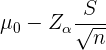
y para esta muestra tenemos que  ,
,  ,
,  y
y  . Al tratarse de un contraste unilateral, entonces sólo consideramos el límite inferior (ya que el superior será
. Al tratarse de un contraste unilateral, entonces sólo consideramos el límite inferior (ya que el superior será  ). Además, para una significancia de
). Además, para una significancia de  el valor crítico asociado es
el valor crítico asociado es 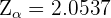 . Luego, tenemos que el intervalo de confianza es
. Luego, tenemos que el intervalo de confianza es
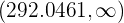
Y como  no está dentro del intervalo de confianza, entonces el criterio de rechazo de cumple.
no está dentro del intervalo de confianza, entonces el criterio de rechazo de cumple.
En consecuencia, rechazamos la hipótesis nula. Por tanto, aceptamos las sospechas del control de calidad de que el tiempo de duración de las baterías es menor a 300 minutos (con una confianza del 2%).
14 Se cree que el nivel medio de protombina en una población normal es de 20 mg/100 ml de plasma con una desviación típica de 4 miligramos/100 ml. Para comprobarlo, se toma una muestra de 40 individuos en los que la media es de 18.5 mg/100 ml. ¿Se puede aceptar la hipótesis, con un nivel de significación del 5%?
En este caso se trata de una prueba de hipótesis donde buscamos verificar que la media sea igual a cierto valor. De este modo, la hipótesis nula es
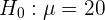
mientras que la hipótesis alternativa es
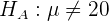
donde el valor hipotético es 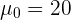
Debido a que estamos haciendo una prueba para la media y siendo un contraste bilateral, el intervalo de confianza se calcula utilizando
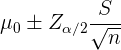
donde 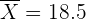 ,
, 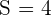 ,
,  y
y 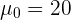 . Para la significancia de
. Para la significancia de  tenemos que
tenemos que 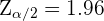 . Por lo que el intervalo de confianza es
. Por lo que el intervalo de confianza es

Luego, como 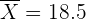 no está dentro del intervalo de confianza, entonces rechazamos la hipótesis nula.
no está dentro del intervalo de confianza, entonces rechazamos la hipótesis nula.
Por tanto, concluimos que el nivel medio de protombina no es de 20 mg / 100 ml plasma.
15 Un productor de manzanas vende su cosecha en cajas de 25 kg con una desviación típica de 1 kg. Para comprobarlo, se toma una muestra de 30 cajas los que la media es de 24.5 kg. ¿Se puede aceptar la hipótesis, con un nivel de significación del 2%?
En este caso se trata de una prueba de hipótesis donde buscamos verificar que la media sea igual a cierto valor. De este modo, la hipótesis nula es
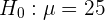
mientras que la hipótesis alternativa es

donde el valor hipotético es 
Debido a que estamos haciendo una prueba para la media y siendo un contraste bilateral, el intervalo de confianza se calcula utilizando
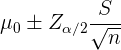
donde  ,
, 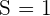 ,
, 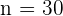 y
y  . Para la significancia de
. Para la significancia de  tenemos que
tenemos que  . Por lo que el intervalo de confianza es
. Por lo que el intervalo de confianza es
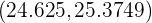
Luego, como  no está dentro del intervalo de confianza, entonces rechazamos la hipótesis nula.
no está dentro del intervalo de confianza, entonces rechazamos la hipótesis nula.
Por tanto, concluimos que el peso medio de cada caja de manzana no es de 25 kilogramos.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En la siguiente tabla se presentan las cantidades promedio de jugo de frutas que empacan, en bolsas de litro, tres máquinas empacadas de una agroindustria.
-MAQUINAS
A
B
C
-PROMEDIO EMPACADO POR BOLSA
1.039 LTS
0.989 LTS
1.090 LTS
-DESVIACIÓN ESTANDAR
0.332 LTS
0.350 LTS
0.371 LTS
¿Cuál de las 3 máquinas tiene la cantidad promedio de empacado por bolsa más confiable? ¿Por qué?
ejercicio. En una ciudad de 100.000 habitantes, se quiere estimar la proporción de personas que utilizan bicicleta como medio de transporte. ¿Cuántas personas deben incluirse en la muestra para obtener un margen de error del 5% con un nivel de confianza del 95%?
10.- Las estaturas de cierta población se distribuyen N(168,8). Calcula la probabilidad de que en una muestra de 36 personas la altura media no difiera de la de la población en más de 1 cm.
28 28 28 28 24 24 20 20 20 20 20 25 25 25 27 27 27 26 22 22 22
En una escuela de 150 estudiantes se requiere realizar una investigación sobre las preferencias de las áreas de los estudiantes y se debe calcular su muestra para conocer cuántos estudiantes se le debe aplicar la encuesta, determinando que el grado de confianza es del 95%, la probabilidad de éxito de 98% y el error de calculo del 6%.
Caso de estudio: En el Perú, el Ministerio de Salud (MINSA) está interesado en conocer la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. Para ello, el MINSA decide realizar una encuesta a una muestra de adolescentes de esta población.
Objetivo:
El objetivo del caso de estudio es que los estudiantes apliquen la fórmula para estimar una proporción poblacional para estimar la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. También, debe indicar el tipo de muestreo probabilístico que deberá emplear.
¿Cuál debe ser el tamaño de muestra para estimar la prevalencia de la depresión, con un nivel de confianza del 95%, margen de error de 4%, e indica el método de selección de la muestra
La experiencia con los trabajado indica que el tiempo requerido para que un trabajador cualquiera termine un trabajo, es una variable con distribución aproximada a la normal con una media de 145 minutos y una desviación estándar de 12 minutos. Se lleva a cabo un programa de capacitación con el propósito de mejorar la destreza de los trabajadores y disminuir así el tiempo medio. Para verificar los resultados de dicho programa se toma al azar una muestra de 16 trabajadores y si esta muestra arroja un tiempo medio mayor que 139 minutos se aceptará la hipótesis de que el tiempo medio sigue siendo de 145 minutos. Pruebe la hipótesis con un nivel de significancia del 5%.
Una empresa de seguros ha estado aplicando diferentes técnicas para incrementar sus ventas durante los últi mos 6 meses. El promedio de ventas por semestre es de 54 ventas diarias, con una muestra aleatoria de 60 días de los últimos 6 meses, se obtiene que en promedio hay 60 ventas diarias con una desviación estándar de 28 Con un nivel de significación de 5%, es posible asegu rar que el promedio de ventas aumento?
A una muestra aleatoria de 150 alumnos de la universidad, se le preguntó si había estudiado el idioma inglés. 75 respondieron Sí, 55 respondieron No y 20 no opinaron. a. ¿Cuál es el valor de la estimación puntual de la proporción de la población que responde Sí?. b. ¿Cuál es el valor de la estimación puntual de la proporción de la población que respondió No?. c. Encuentre el intervalo de confianza del 90% para la proporción poblacional que respondieron Sí. Fuente de ingresos Frecuencia Propina sólo domingos 149 Quehaceres, dádivas y domingos 219 Quehaceres y dádivas, no domingos 251 Nada 165 T o t a l 784
Se quiere hacer un estudio para conocer el número de mujeres casadas que van a consulta ginecológicas en una población, por estudios anteriores se sabe que la desviación estándar de 1 mujeres, el investigador considera que el margen de error es de 9% y el coeficiente de confianza es de 91%.