Temas

Intervalo de confianza para una proporción
Cada miembro de una población en estudio puede clasificarse dependiendo de cierta característica de interés, puede clasificarse como que tiene o no tiene dicha característica, y podemos estar interesados en la proporción de personas " " de la población que tienen esa característica.
" de la población que tienen esa característica.
Si tomamos una muestra aleatoria de tamaño  de la población y denotamos con
de la población y denotamos con  a la variable aleatoria que representa el numero de elementos de la muestra con la característica de interés, entonces se tendrá que
a la variable aleatoria que representa el numero de elementos de la muestra con la característica de interés, entonces se tendrá que  es una variable aleatoria que sigue una distribución binomial con parámetros
es una variable aleatoria que sigue una distribución binomial con parámetros  y
y  (por lo tanto, la esperanza y varianza son:
(por lo tanto, la esperanza y varianza son: 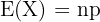 y
y 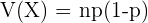 ) . Y si el tamaño de la muestra es grande entonces tendremos que
) . Y si el tamaño de la muestra es grande entonces tendremos que

se distribuye como una normal estándar.
Ahora bien, esto nos ayuda a encontrar un intervalo de nivel de confianza  para la proporción poblacional, para esto partimos de que
para la proporción poblacional, para esto partimos de que

y de aquí llegamos a que el intervalo de confianza esta determinado por

donde  , es decir
, es decir  proporción de individuos con dicha característica en las muestras de tamaño
proporción de individuos con dicha característica en las muestras de tamaño  .
.
Intervalo de confianza para una proporción

Ejemplo de calcular intervalo de confianza de proporciones
En una muestra de  personas extraída de una población,
personas extraída de una población,  de ellas son portadoras de cierta enfermedad. Estima un intervalo de confianza a un nivel del
de ellas son portadoras de cierta enfermedad. Estima un intervalo de confianza a un nivel del  % para la proporción de personas portadoras de la enfermedad.
% para la proporción de personas portadoras de la enfermedad.
Tenemos que

para

entonces

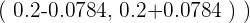
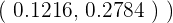













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
ejercicio. En una ciudad de 100.000 habitantes, se quiere estimar la proporción de personas que utilizan bicicleta como medio de transporte. ¿Cuántas personas deben incluirse en la muestra para obtener un margen de error del 5% con un nivel de confianza del 95%?
10.- Las estaturas de cierta población se distribuyen N(168,8). Calcula la probabilidad de que en una muestra de 36 personas la altura media no difiera de la de la población en más de 1 cm.
28 28 28 28 24 24 20 20 20 20 20 25 25 25 27 27 27 26 22 22 22
En una escuela de 150 estudiantes se requiere realizar una investigación sobre las preferencias de las áreas de los estudiantes y se debe calcular su muestra para conocer cuántos estudiantes se le debe aplicar la encuesta, determinando que el grado de confianza es del 95%, la probabilidad de éxito de 98% y el error de calculo del 6%.
Caso de estudio: En el Perú, el Ministerio de Salud (MINSA) está interesado en conocer la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. Para ello, el MINSA decide realizar una encuesta a una muestra de adolescentes de esta población.
Objetivo:
El objetivo del caso de estudio es que los estudiantes apliquen la fórmula para estimar una proporción poblacional para estimar la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. También, debe indicar el tipo de muestreo probabilístico que deberá emplear.
¿Cuál debe ser el tamaño de muestra para estimar la prevalencia de la depresión, con un nivel de confianza del 95%, margen de error de 4%, e indica el método de selección de la muestra
La experiencia con los trabajado indica que el tiempo requerido para que un trabajador cualquiera termine un trabajo, es una variable con distribución aproximada a la normal con una media de 145 minutos y una desviación estándar de 12 minutos. Se lleva a cabo un programa de capacitación con el propósito de mejorar la destreza de los trabajadores y disminuir así el tiempo medio. Para verificar los resultados de dicho programa se toma al azar una muestra de 16 trabajadores y si esta muestra arroja un tiempo medio mayor que 139 minutos se aceptará la hipótesis de que el tiempo medio sigue siendo de 145 minutos. Pruebe la hipótesis con un nivel de significancia del 5%.
Una empresa de seguros ha estado aplicando diferentes técnicas para incrementar sus ventas durante los últi mos 6 meses. El promedio de ventas por semestre es de 54 ventas diarias, con una muestra aleatoria de 60 días de los últimos 6 meses, se obtiene que en promedio hay 60 ventas diarias con una desviación estándar de 28 Con un nivel de significación de 5%, es posible asegu rar que el promedio de ventas aumento?
A una muestra aleatoria de 150 alumnos de la universidad, se le preguntó si había estudiado el idioma inglés. 75 respondieron Sí, 55 respondieron No y 20 no opinaron. a. ¿Cuál es el valor de la estimación puntual de la proporción de la población que responde Sí?. b. ¿Cuál es el valor de la estimación puntual de la proporción de la población que respondió No?. c. Encuentre el intervalo de confianza del 90% para la proporción poblacional que respondieron Sí. Fuente de ingresos Frecuencia Propina sólo domingos 149 Quehaceres, dádivas y domingos 219 Quehaceres y dádivas, no domingos 251 Nada 165 T o t a l 784
Se quiere hacer un estudio para conocer el número de mujeres casadas que van a consulta ginecológicas en una población, por estudios anteriores se sabe que la desviación estándar de 1 mujeres, el investigador considera que el margen de error es de 9% y el coeficiente de confianza es de 91%.