Temas
¿Qué es la estimación puntual?
Una estimación puntual es un número que calculamos a partir de una muestra. Este número se conoce como estadística o estadístico. Así, utilizamos esta estadística para hacer la estimación del parámetro correspondiente de la población.
Ejemplo: Se realiza una encuesta a 500 jóvenes entre 8 y 25 años de la ciudad de Tarifa, en el sur de España. En la encuesta se indica que el 89% de los jóvenes practica Kitesurf. Como no se ha cuestionado a todos los jóvenes de la ciudad, entonces decimos que 89% es una estimación puntual del verdadero porcentaje de la problación.
Por tanto, podemos decir que alrededor del 89% de los jóvenes de la ciudad de Tarifa practican Kitesurf.
Ejemplo: Se mide el tiempo de vida de 40 bombillas de 60 W de cierto lote. Al calcular el promedio del tiempo de vida, se obtiene 
horas. Como no se midió el tiempo de vida para todas las 1.000 bombillas del lote, entonces 
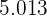es una estimación puntual para el tiempo de vida media del lote.
¿Qué es el error de muestreo?
La posibilidad de un error de muestreo existe siempre.
El error de muestreo es la diferencia entre una estadística que se calcula de una muestra, y el valor del parámetro correspondiente en la población. Como el error siempre es positivo, entonces se toma el valor absoluto de esta diferencia.
Es importante poder manejar este error de muestreo en el proceso de decisión. Al fin y al cabo, el objetivo de muchas de las herramientas estadísticas que aprendemos es apoyarnos al momento de una toma de decisiones.
Una característica del error de muestreo es que este es menor cuando el tamaño de muestra aumenta. Por este motivo se sugiere que el tamaño de muestra sea tan grande como se permita.
Por ejemplo, la estatura media de las mujeres de España es 163,4 cm, y supongamos que, al tomar una muestra de 1.000 mujeres, obtenemos una estatura promedio de 164,6. Entonces, el error de muestreo es
Es decir, el error de muestreo fue de 1,2 cm.
¿Qué es el intervalo de confianza?
Por lo general, el error de muestreo no se puede eliminar. Por tanto, utilizamos un intervalo de confianza para poder manejar el error.
Definición de un intervalo de confianza
Definamos una probabilidad 
. Deseamos construir un intervalo tal que el parámetro real de la población esté dentro del intervalo con una probabilidad . Este intervalo se define con dos números 
y 
y se conoce como intervalo de confianza con nivel de confianza . Se suele denotar al intervalo como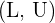 
El intervalo de confianza se construye a partir del estadístico muestral. Además, la probabilidad se suele denotar como 
, en donde 
se conoce como el nivel de significación.
Ejemplo: Supongamos que, en el ejemplo de las bombillas de 60 W, el intervalo de confianza del 95% es 
. Por tanto, sabemos que existe un 95% de probabilidad de que el tiempo de vida promedio de todo el lote esté entre las 4.799 y las 5.227 horas.
Variación del intervalo de confianza
Recordemos que la desviación estándar 
es una medida de la variación de los datos en la población o muestra. Así, será pequeña si todos los datos son muy similares entre sí; por otro lado, será grande si los datos varían mucho entre sí.
La desviación estándar de una población/muestra finita se calcula mediante
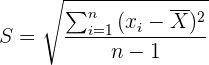
en donde 
es el promedio de la muestra y 
es el número de elementos en la muestra. La desviación estándar de la población se denota mediante 
, mientras que la desviación de la muestra se denota como .
Notemos que si obtenemos una muestra 
, entonces la estimación de la media sería . Sin embargo, si tomamos otra muestra diferente 
, la estimación será 
. Es decir, las estimaciones puntuales también varían; por lo tanto, tiene sentido definir la desviación estándar para los estimadores.
En general, si conocemos la desviación estándar de la población original, entonces la desviación estándar del promedio es
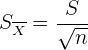
donde es el tamaño de la muestra . Para los estimadores puntuales, la desviación estándar se suele llamar error estándar.
A partir de la ecuación de arriba, podemos observar que si el tamaño de muestra aumenta, entonces la desviación 
de la estimación disminuirá. En otras palabras, entre más grande sea la muestra, más cercanas serán las posibles estimaciones; de hecho, entre más grande sea la muestra, más cercana será la estimación al valor real del parámetro de la población.
Recordemos que denota la desviación estándar de la población/muestra, mientras que denota el error estándar (o desviación estándar) de la estimación.
No te dejes nada en el tintero gracias a nuestras clases particulares matematicas.
¿Cómo se calcula el intervalo de confianza?
Existen distintas formas de calcular los intervalos de confianza; cada una depende de la información que tengamos disponible.
Desviación estándar conocida y tamaño de muestra mayor a 30
Supongamos que tenemos una población , cuyo tamaño de muestra es mayor o igual a 30, es decir, 
. Además, supongamos que sabemos que la desviación estándar de la población es . Entonces, el intervalo de confianza para la media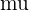 
con un nivel de confianza de se calcula de la siguiente manera:
1 Calcula el promedio de la muestra,
2 Determina el error estándar de la estimación,
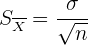
3 Encuentra el valor crítico 
tal que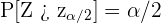 
.
Si tenemos una variable 
con distribución estándar, entonces es aquél valor tal que la probabilidad de que sea mayor a es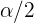 
. No es sencillo encontrar estos valores de forma analítica, por tanto se utilizan tablas o software para encontrarlos.
La tabla de los valores de para las más comunes se encuentra más abajo.
4 Calcula el intervalo de confianza utilizando
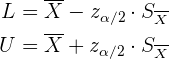
En algunos sitios se suele resumir el intervalo de confianza para este caso como
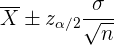
Esta expresión indica tanto el límite inferior como el límite superior.
Ejemplo: Retomando el ejemplo de las bombillas de 60 W. Se tomó una muestra de 40 bombillas donde el tiempo de vida promedio fue . Se tiene la información de que la desviación estándar del tiempo de vida es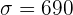 
horas. Entonces, para calcular el intervalo de confianza al 95%, primero debemos notar que 
. Así, tenemos que
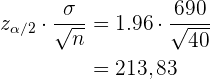
De este modo, el intervalo de confianza es
Observemos que en el ejemplo anterior, calculamos primero la cantidad
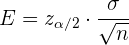
Este valor se conoce como margen de error o error de estimación.
Dicho esto, hay una probabilidad de de que nuestra estimación tendrá un error de 
como máximo. La importancia de los intervalos de confianza está en que nos permite estimar también la magnitud del error posible.
Si vives en la capital y buscas un profesor particular matematicas madrid, lo encontrarás en Superprof.
Desviación estándar desconocida
En el caso de que no conozcamos la desviación estándar de la población original, entonces debemos utilizar una estrategia ligeramente diferente para calcular el intervalo de confianza.
El procedimiento para calcular el intervalo de confianza es:
1 Calcula el promedio de la muestra,
2 Determina el error estándar de la muestra,
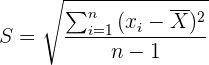
3 Encuentra el valor crítico 
tal qu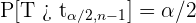e 
donde 
sigue una distribución 
de Student con 
grados de libertad.
En este caso tenemos una variable con distribución de Student con grados de libertad. De este modo, es aquél valor tal que la probabilidad de que sea mayor a es 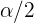. De nuevo, no es sencillo encontrar estos valores de forma analítica, por tanto se utiliza software para encontrarlos.
4 Calcula el intervalo de confianza utilizando
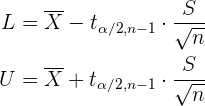
En este caso, el intervalo de confianza se resume como
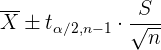
Ejemplo: Consideremos de nuevo el ejemplo de las bombillas de 60 W. Recordemos que se tomó una muestra de 40 bombillas donde el tiempo de vida promedio fue .
Sin embargo, en este caso no sabemos la desviación estándar de la población. No obstante, al calcular la desviación estándar de las 40 bombillas, obtenemos que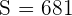 
horas. Entonces, para calcular el intervalo de confianza al 95%, primero debemos obtener el cual es el valor crítico de una distribución con 39 grados de libertad. Utilizando software, obtenemos que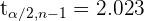 
.
Así, tenemos que
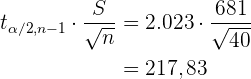
De este modo, el intervalo de confianza es
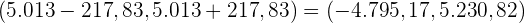
Cuando la desviación estándar es desconocida, el margen de error se calcula utilizando
Tablas de valores críticos y uso de software estadístico
Como se puede apreciar, para determinar los intervalos de confianza se necesitan obtener los valores críticos; ya sea de una distribución normal o de una distribución t de Student.
En el caso de una distribución normal, los valores son muy conocidos y se resumen en la siguiente tabla, para valores de comunes:
| | |
|---|---|---|
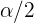| 0.90 | 0.05 | 1.645 |
| 0.95 | 0.025 | 1.96 |
| 0.99 | 0.005 | 2.575 |
No obstante, estos valores se pueden conseguir utilizando software. De hecho, en el caso de la distribución t de Student, no es sencillo resumir los valores críticos en una tabla ya que estos valores son diferentes según los grados de libertad 
.
En la siguiente lista se muestran algunas formas de obtener los valores críticos:
1 Para obtener el valor de con Excel, se utiliza la función
en donde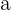 
es el valor de .
2 También se puede obtener el valor utilizando el software estadístico R. En este caso, la función a utilizar es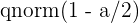 
. De forma similar, 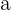debe tomar el valor que tiene .
3 Para el caso de la distribución de Student, para obtener 
con Excel, se utiliza la función
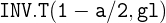
en donde 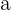es el valor de y 
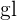son los grados de libertad .
4 Por último, para obtener el valor utilizando R se utiliza la función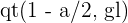 
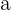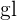. Al igual que en el caso anterior, toma el valor que tiene y son los grados de libertad .
Impacto del cambio de los parámetros en el intervalo de confianza
Algo que podemos notar es que, al realizar la estimación con intervalos de confianza, nosotros asignamos de forma arbitraria el tamaño de muestra y el nivel de confianza .
Por lo regular, estos parámetros se asignan tomando en cuenta la precisión con la que deseamos la estimación. Por ejemplo, si deseamos una precisión muy precisa y confiable, entonces requerimos que sea grande y que el error sea pequeño; en este caso requerimos que también sea grande. Por otro lado, si por cuestiones de falta de recursos o tiempo no podemos tomar una muestra demasiado grande, entonces podemos ajustar para que sea más pequeña; en este caso, nuestra estimación será menos confiable.
A continuación discutimos el impacto de estos parámetros en los intervalos de confianza.
¿Qué pasa cuando cambiamos el nivel de confianza?
Observemos que el margen de error está dado por la expresión
Algo que debemos notar es que y aumentan cuando el nivel de confianza aumenta. Por tanto, podemos reducir el nivel de confianza para reducir el tamaño de error; sin embargo, esto implica que hay menos confianza en el intervalo. En otras palabras, es más probable que tu estimación se encuentre fuera del intervalo de confianza.
¿Qué pasa cuando cambiamos el tamaño de muestra?
Por otro lado, de la misma ecuación del error
podemos observar que cuando aumenta, el tamaño del error disminuye (conservando el mismo nivel de confianza). Por este motivo es que es ideal que el tamaño de muestra sea lo suficientemente grande para poder tener un margen de error pequeño y un alto nivel de confianza.
Tamaño de muestra necesario
Si despejamos de , obtenemos
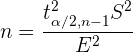
Así, si tenemos un error deseado , podemos calcular el tamaño de muestra necesario para que nuestra estimación no supere ese error.
Para hacer eso, primero es necesario tomar una muestra pequeña (dependiendo el contexto, incluso 15 elementos son suficientes). Con esto, estimamos el tamaño de muestra necesario para que nuestro error sea menor a . Luego, volvemos a tomar una muestra pero ahora con un tamaño de muestra .
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En la siguiente tabla se presentan las cantidades promedio de jugo de frutas que empacan, en bolsas de litro, tres máquinas empacadas de una agroindustria.
-MAQUINAS
A
B
C
-PROMEDIO EMPACADO POR BOLSA
1.039 LTS
0.989 LTS
1.090 LTS
-DESVIACIÓN ESTANDAR
0.332 LTS
0.350 LTS
0.371 LTS
¿Cuál de las 3 máquinas tiene la cantidad promedio de empacado por bolsa más confiable? ¿Por qué?
ejercicio. En una ciudad de 100.000 habitantes, se quiere estimar la proporción de personas que utilizan bicicleta como medio de transporte. ¿Cuántas personas deben incluirse en la muestra para obtener un margen de error del 5% con un nivel de confianza del 95%?
10.- Las estaturas de cierta población se distribuyen N(168,8). Calcula la probabilidad de que en una muestra de 36 personas la altura media no difiera de la de la población en más de 1 cm.
28 28 28 28 24 24 20 20 20 20 20 25 25 25 27 27 27 26 22 22 22
En una escuela de 150 estudiantes se requiere realizar una investigación sobre las preferencias de las áreas de los estudiantes y se debe calcular su muestra para conocer cuántos estudiantes se le debe aplicar la encuesta, determinando que el grado de confianza es del 95%, la probabilidad de éxito de 98% y el error de calculo del 6%.
Caso de estudio: En el Perú, el Ministerio de Salud (MINSA) está interesado en conocer la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. Para ello, el MINSA decide realizar una encuesta a una muestra de adolescentes de esta población.
Objetivo:
El objetivo del caso de estudio es que los estudiantes apliquen la fórmula para estimar una proporción poblacional para estimar la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. También, debe indicar el tipo de muestreo probabilístico que deberá emplear.
¿Cuál debe ser el tamaño de muestra para estimar la prevalencia de la depresión, con un nivel de confianza del 95%, margen de error de 4%, e indica el método de selección de la muestra
La experiencia con los trabajado indica que el tiempo requerido para que un trabajador cualquiera termine un trabajo, es una variable con distribución aproximada a la normal con una media de 145 minutos y una desviación estándar de 12 minutos. Se lleva a cabo un programa de capacitación con el propósito de mejorar la destreza de los trabajadores y disminuir así el tiempo medio. Para verificar los resultados de dicho programa se toma al azar una muestra de 16 trabajadores y si esta muestra arroja un tiempo medio mayor que 139 minutos se aceptará la hipótesis de que el tiempo medio sigue siendo de 145 minutos. Pruebe la hipótesis con un nivel de significancia del 5%.
Una empresa de seguros ha estado aplicando diferentes técnicas para incrementar sus ventas durante los últi mos 6 meses. El promedio de ventas por semestre es de 54 ventas diarias, con una muestra aleatoria de 60 días de los últimos 6 meses, se obtiene que en promedio hay 60 ventas diarias con una desviación estándar de 28 Con un nivel de significación de 5%, es posible asegu rar que el promedio de ventas aumento?
A una muestra aleatoria de 150 alumnos de la universidad, se le preguntó si había estudiado el idioma inglés. 75 respondieron Sí, 55 respondieron No y 20 no opinaron. a. ¿Cuál es el valor de la estimación puntual de la proporción de la población que responde Sí?. b. ¿Cuál es el valor de la estimación puntual de la proporción de la población que respondió No?. c. Encuentre el intervalo de confianza del 90% para la proporción poblacional que respondieron Sí. Fuente de ingresos Frecuencia Propina sólo domingos 149 Quehaceres, dádivas y domingos 219 Quehaceres y dádivas, no domingos 251 Nada 165 T o t a l 784
Se quiere hacer un estudio para conocer el número de mujeres casadas que van a consulta ginecológicas en una población, por estudios anteriores se sabe que la desviación estándar de 1 mujeres, el investigador considera que el margen de error es de 9% y el coeficiente de confianza es de 91%.