¡Bienvenidos a nuestra página dedicada a ejercicios y problemas de estadística! Hemos desarrollado está página ti. ¡Pon a prueba tus conocimientos sobre estadística descriptiva!
La estadística es una disciplina que se ocupa de recolectar, organizar, analizar e interpretar datos para extraer información significativa y tomar decisiones fundamentadas. Se basa en métodos y técnicas matemáticas para recopilar información numérica o descriptiva sobre una población o muestra en particular.
La estadística desempeña un papel crucial en una amplia gama de campos, como la economía, la ciencia, la salud, la investigación de mercado y muchas otras áreas donde se requiere el análisis de datos. Su objetivo principal es descubrir patrones, tendencias y relaciones entre variables, lo que permite comprender mejor el mundo que nos rodea y tomar decisiones informadas.
En este espacio, exploraremos los desafíos y las soluciones que presenta el fascinante mundo de la estadística. Aquí exploraremos distintas técnicas para analizar datos efectivamente. Tales técnicas incluyen calcular la desviación típica, la varianza, la medina, media, moda, etc. de conjuntos de datos. Superprof te invita a que resuelvas los siguientes ejercicios y problemas sobre estadística. ¡Perfecciona tus habilidades!
A un conjunto de 
números cuya media es 
se le añaden los números 
y 
. ¿Cuál es la media del nuevo conjunto de números?
La media del conjunto de los números es
Entonces
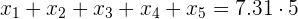
La media de los 
números es
Que es lo mismo que
Un dentista observa el número de caries en cada uno de los 
niños de cierto colegio. La información obtenida aparece resumida en la siguiente tabla:
| Nº de caries |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
-
- Completar la tabla obteniendo los valores , , .
- Completar la tabla obteniendo los valores
-
- Hacer un diagrama de sectores.
-
- Calcular el número medio de caries.
1Tabla
La suma de las frecuencias relativas ha de ser igual a :
La frecuencia relativa de un dato es igual su frecuencia absoluta dividida entre , que es la suma de las frecuencias absolutas.
| Nº de caries (xi) | | |  |
| | | |
| | | |
|  |  |  |
| | |  |
| | | |
|  |
2Diagrama de sectores
Calculamos los grados que corresponden a una unidad de frecuencia absoluta
Calculamos los grados que corresponden a cada frecuencia absoluta.
3Media aritmética
Se tiene el siguiente conjunto de 
datos:
Obtener su mediana y cuartiles.
1 Ordenar los datos
En primer lugar ordenamos los datos de menor a mayor:
2 Mediana
Como el número de datos es par, la mediana es la media de las dos puntuaciones centrales:
3 Cuartiles
Para obtener el primer cuartil, dividimos el número de datos entre
Localizamos el dato número 
y en posición, y tomamos el promedio
El segundo cuartil es la mediana
Para el tercer cuartil, el número de datos lo multiplicamos por y lo dividimos entre
Localizamos el dato 
y en posición, y tomamos el promedio
Un pediatra obtuvo la siguiente tabla sobre los meses de edad de 
niños de su consulta en el momento de andar por primera vez:
| Meses | Niños |
 | |
 | |
 | |
 |  |
 | |
 |  |
| |
-
- Dibujar el polígono de frecuencias.
-
- Calcular la moda, la mediana, la media y la varianza
1 Polígono de frecuencias
2 Completar la tabla
Completamos la tabla con:
La frecuencia acumulada 
para calcular la mediana.
El producto de la variable por su frecuencia absoluta 
para calcular la media.
El producto de la variable al cuadrado por su frecuencia absoluta 
para calcular la varianza y la desviación típica.
 | |  | | |
| | | |  |
| | |  |  |
| | |  |  |
| |  |  |  |
| |  |  |  |
| |  |  |  |
| | | |  |
|  |  |
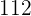3 Moda
La moda es el valor que tiene mayor frecuencia absoluta
Miramos en la columna de las y la frecuencia absoluta mayor 
corresponde a
4 Mediana
Para calcular la mediana dividimos 
entre y vemos que la casilla de las donde se encuentra el dato corresponde a
5 Media aritmética
Calculamos la sumatoria de la variable por su frecuencia absoluta 
que es y la dividimos por 
6 Varianza
Calculamos la sumatoria de 
, la dividimos por y al resultado le restaremos la media aritmética al cuadrado 
Completar los datos que faltan en la siguiente tabla estadística:
| | | |
| |  | |
| | ||
| |  | |
| |  | |
| |  | |
|  | ||
| | | |
|
Calcular la media, mediana y moda de esta distribución.
1 Tabla
-
Primera fila
La primera frecuencia acumulada coincide con la primera frecuencia absoluta
La primera frecuencia relativa acumulada 
es igual a la primera frecuencia absoluta 
dividida por 
Entonces es el número total de datos
-
Segunda fila
La segunda frecuencia acumulada será igual a la frecuencia acumulada anterior más la frecuencia absoluta correspondiente
La frecuencia relativa acumulada 
es igual a la frecuencia absoluta dividida entre
-
Tercera fila
Para hallar la frecuencia absoluta podemos hacerlo de dos modos
1. Por medio de la frecuencia relativa acumulada:
2. La frecuencia absoluta será la diferencia entre 
y 
-
Cuarta fila
La frecuencia acumulada será igual a la frecuencia acumulada anterior más la frecuencia absoluta correspondiente 
-
Quinta fila
La frecuencia relativa acumulada 
es igual a la frecuencia absoluta 
dividida entre
-
Sexta fila
De manera análoga a la tercera fila, tendremos dos maneras de hacerlo
La frecuencia absoluta será igual a la frecuencia acumulada 
menos la frecuencia acumulada anterior 
, es decir, la diferencia entre 
y 
La frecuencia relativa acumulada 
es igual a la frecuencia absoluta 
dividida entre
-
Séptima fila
La frecuencia relativa acumulada 
es igual a la frecuencia absoluta dividida entre
-
Octava fila
La ultima frecuencia acumulada coincide con
La frecuencia absoluta será igual a la frecuencia acumulada 
menos la frecuencia acumulada anterior 
, es decir, la diferencia entre 
y 
La frecuencia relativa acumulada 
es igual a la frecuencia absoluta dividida entre
2 Completar la tabla
Con los datos obtenidos completamos la tabla. Además añadimos la columna del producto de la variable por su frecuencia absoluta, para calcular la media
| | | |  |
| | | | |
| | | | |
| | | |  |
| |  | | |
| | |  | |
| | | |  |
| | | | |
| | | | |
|  |
3 Media artmética
Calculamos la sumatoria de la variable por su frecuencia absoluta 
que es y la dividimos por
4 Mediana
Para calcular la mediana dividimos entre y vemos que la casilla de las donde se encuentra corresponde a
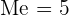
5 Moda
La moda es el valor que tiene mayor frecuencia absoluta
Miramos en la columna de las y la frecuencia absoluta mayor corresponde a
Considérense los siguientes datos: 
. Se pide:
-
- Calcular su media y su varianza.
-
- Si todos los datos anteriores los multiplicamos por 3, cúal será la nueva media y varianza.
Calcular su media y su varianza
1 Media
Ordenamos los datos
.
Sumamos los valores y lo dividimos entre el número total de datos que hay.
2 Varianza
Tomamos el promedio de los cuadrados de los números y le restamos el cuadrado de la media
Al multiplicar por ...
1 Media
Si todos los valores de la variable se multiplican por la media aritmética queda multiplicada por
2 Varianza
Si todos los valores de la variable se multiplican por la varianza queda multiplicada por al cuadrado
El resultado de lanzar dos dados 
veces viene dado por la tabla:
| Sumas | Veces |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
-
- Calcular la media y la desviación típica.
-
- Hallar el porcentaje de valores comprendidos en el intervalo
.
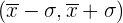- Hallar el porcentaje de valores comprendidos en el intervalo
1 Completar la tabla
Completamos la tabla con:
El producto de la variable por su frecuencia absoluta para calcular la media.
El producto de la variable al cuadrado por su frecuencia absoluta para calcular la desviación típica.
| | |  |
| | | |
| | |  |
| |  |  |
| |  |  |
| | |  |
| |  |  |
| |  |  |
| |  |  |
| |  |  |
| |  |  |
| |  |  |
|  |  |
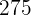2 Media aritmética
Hemos añadido la columna porque queremos hallar su sumatoria 
, que después dividiremos por 
para obtener la media
3 Desviación típica
Hemos añadido la columna porque queremos hallar su sumatoria 
, que después dividiremos por 
y al resultado le restaremos la media aritmética al cuadrado 
, y por último haremos la raíz cuadrada del resultado obtenido
4 Porcentaje
Conociendo la desviación típica, calculamos el intervalo mencionado.
Los valores comprendidos en el intervalo 
son los correspondientes a las sumas de 
. Sumamos sus frecuencias absolutas.
Hallamos el porcentaje mediante la siguiente proporción:
Las alturas de los jugadores de un equipo de baloncesto vienen dadas por la tabla:
| Altura | Nº de jugadores |
 | |
 | |
 | |
 | |
 | |
 | |
Calcular:
-
- La media.
-
- La mediana.
-
- La desviación típica.
-
- ¿Cuántos jugadores se encuentran por encima de la media más una desviación típica?
1 Completar la tabla
Completamos la tabla con:
La frecuencia acumulada para calcular la mediana
El producto de la variable por su frecuencia absoluta para calcular la media
El producto de la variable al cuadrado por su frecuencia absoluta 
para calcular la varianza y la desviación típica
| | | | | |
 |  | | | |  |
 |  | | |  |  |
 |  | | |  |  |
 |  | | | |  |
 |  | |  |  |  |
 |  | | |  |  |
|  |  |
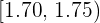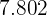2 Media
Calculamos la sumatoria de la variable por su frecuencia absoluta que es y la dividimos por 
3 Mediana
Buscamos el intervalo donde se encuentra la mediana, para ello dividimos la por porque la mediana es el valor central
Buscamos en la columna de las frecuencias acumuladas el intervalo que contiene a 
Aplicaremos la fórmula para el cálculo de la mediana para datos agrupados, extrayendo los siguientes datos:
De este moda la mediana es
4 Desviación típica
Calculamos la sumatoria de 
, la dividimos por 
y al resultado le restaremos la media aritmética al cuadrado 
. Por último realizamos la raíz cuadrado del resultado
De este modo
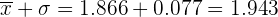
Este valor pertenece a un percentil que se encuentra en el penúltimo intervalo.
Establecemos la siguiente proporción:
Sólo hay 3 jugadores por encima de 
Los resultados al lanzar un dado 200 veces vienen dados por la siguiente tabla:
| | | | | | |
|  |  | |  |  | |
Determinar y sabiendo que la puntuación media es 
.
1 Completar la tabla
Realizamos la sumatoria de y de
| | |
| | |
| |  |
| |  |
| |  |
| |  |
| |  |
 |  |
2 Obtener ecuaciones
La sumatoria de las frecuencias absolutas es igual a 
De esto podemos concluir que
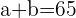
La sumatoria de los dividida entre 
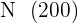es la media
De lo que podemos concluir que
3 Resolvemos el sistema
Resolvemos el sistema de ecuaciones por reducción
Finalmente
El histograma de la distribución correspondiente al peso de alumnos de Bachillerato es el siguiente:
-
- Formar la tabla de la distribución.
-
- Si Andrés pesa kg, ¿cuántos alumnos hay menos pesados que él?
- Si Andrés pesa
-
- Calcular la moda.
-
- Hallar la mediana.
-
- ¿A partir de que valores se encuentran el
de los alumnos más pesados?
- ¿A partir de que valores se encuentran el
1 Tabla de distribución
| | | |
 |  | | |
 |  |  | |
 |  |  |  |
 |  |  |  |
 |  | | |
|
2 Alumnos menos pesados que Andrés
Notamos que los primeros cuatro intervalos constituyen los alumnos menos pesados que Andrés, así que sumamos sus frecuencias absolutas 
3 Moda
En primer lugar buscamos el intervalo donde se encuentra la moda, que será el intervalo que tenga la mayor frecuencia absoluta
La clase modal es:
Aplicaremos la fórmula para el cálculo de la moda para datos agrupados, extrayendo los siguientes datos:
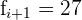
Y así, la moda es igual a
4 Mediana
Buscamos el intervalo donde se encuentra la mediana, para ello dividimos la por porque la mediana es el valor central
Buscamos en la columna de las frecuencias acumuladas el intervalo que contiene a
Aplicaremos la fórmula para el cálculo de la mediana para datos agrupados, extrayendo los siguientes datos:
Calculamos así la mediana
5 Cuartil tercero
El valor a partir del cual se encuentra el de los alumnos más pesados es el cuartil tercero.
Buscamos el intervalo donde se encuentra el tercer cuartil, multiplicando por 
y dividiendo por
Buscamos en la columna de las frecuencias acumuladas el intervalo que contiene a 
La clase de 
es:
Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:
Y así, el tercer cuartil es igual a
De esta distribución de frecuencias absolutas acumuladas, calcular:
| Edad | |
 | |
 | |
 | |
 |  |
 | |
-
- Media aritmética y desviación típica.
-
- ¿Entre qué valores se encuentran las 10 edades centrales?
-
- Representar el polígono de frecuencias absolutas acumuladas.
1 Completar la tabla
Añadimos la columna de las frecuencias absolutas
La primera frecuencia absoluta coincide con la primera frecuencia acumulada, para calcular las siguientes tenemos que restar a la siguiente frecuencia absoluta la anterior
| | | | | |
| | | | | |
| | | | |  |
| | | | |  |
| | | | |  |
| | | |  |  |
|  |  |
2 Media
Hemos añadido la columna porque queremos hallar su sumatoria 
, que después dividiremos por 
para obtener la media
3 Desviación típica
Hemos añadido la columna 
porque queremos hallar su sumatoria 
, que después dividiremos por 
y al resultado le restaremos la media aritmética al cuadrado 
, y por último haremos la raíz cuadrada del resultado obtenido
4 Edades centrales
Veamos que porcentaje representan las edades
Los alumnos representan el central de la distribución.
Debemos hallar 
y 
.
Las edades centrales están en el intervalo: 
.
5 Polígono de frecuencias
Una persona 
mide 
m y reside en una ciudad donde la estatura media es de 
m y la desviación típica es de cm. Otra persona 
mide 
m y vive en una ciudad donde la estatura media es de 
m y la desviación típica es de cm. ¿Cuál de las dos será más alta respecto a sus conciudadanos?
Obtenemos las puntuaciones típicas de estas personas en la distribución que corresponde
Es importante trabajar con las misma unidades por lo que la altura se considerará en centímetros
La puntuación típica de la primera persona es:
La puntuación típica de la segunda persona es:
Al comparar sus puntuaciones, concluímos que la persona es más alta respecto a sus conciudadanos que la persona .
Un profesor ha realizado dos tests a un grupo de alumnos, obteniendo los siguientes resultados: para el primer test la media es y la desviación típica 
.
Para el segundo test la media es y la desviación típica 
.
Un alumno obtiene un en el primero y un en el segundo. En relación con el grupo, ¿en cuál de los dos tests obtuvo mejor puntuación?
Obtenemos las puntuaciones típicas de este alumno en las distribuciones de cada test
La puntuación típica en el primer test es:
La puntuación típica en el segundo test es:
Al comparar la puntuaciones, notamos que en el segundo test consigue mayor puntuación.
La asistencia de espectadores a las salas de un cine un determinado día fue de 
y 
personas.
-
- Calcular la dispersión del número de asistentes.
-
- Calcular el coeficiente de variación.
-
- Si el día del espectador acuden personas más a cada sala, ¿qué efecto tendría sobre la dispersión?
- Si el día del espectador acuden
1 Desviación típica
Obtenemos la media aritmética
Finalmente calculamos la desviación típica
2 Coeficiente de variación
Para calcular el coeficiente de variación debemos dividir la desviación típica entre la media aritmética
3 Dispersión con 50 personas más
Si todas las salas tienen un incremento de personas, la media aritmética también se ve incrementada en personas. Entonces,
La desviación típica no varía, ya que sumamos la misma cantidad a cada dato de la serie.
La dispersión relativa es menor en el segundo caso.
Considere el siguiente conjunto de datos
-
- Calcular la moda.
-
- Calcular la media.
-
- Calcular la mediana.
-
- Calcular los cuartiles.
-
- Calcular la desviación típica.
Primero ordenamos los datos en orden ascendente:
1Moda
La moda es el elemento que más se repide en nuesto conjunto de datos. Así la moda es
2 Mediana
Obtenemos la media aritmética
3 Mediana
La mediana es el dato que separa al conjunto en dos partes iguales. Al tener un conjunto con un número impar de datos, la mediana corresponderá al dato central, en este caso es
4 Cuartiles
Para calcular los cuartiles usaremos la fórmula para un conjunto con un número de elementos impar
donde 
es el número de elementos en el conjunto, en este caso 
Esta fórmula nos da la posición del cuartil.
,
entonces el primer cuartil se encuentra en la cuarta posición de nuestro conjunto ordenado de datos, en este caso, 
,
entonces el segundo cuartil se encuentra en la octava posición de nuestro conjunto ordenado de datos, en este caso, 
De hecho, siempre 
,
entonces el tercer cuartil se encuentra en la doceava posición de nuestro conjunto ordenado de datos, en este caso, 
4 Desviación típica
Para calcular la desviación típica, 
usamos la fórmula
donde es el número de datos y son los datos del conjunto, 
. En nuestro caso, 
y 
. Así tenemos que
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Calcule el segundo cuartil para la tabla de datos dada
IDC f
100 – 134 3
135 – 169 12
170 – 204 19
205 – 239 34
240 – 274 36
275 – 309 19
310 – 344 6
A partir de la siguiente de la siguiente tabla de frecuencia realiza su gráfica número de producto 1 2 3 4 5 frecuencia 35724
Números de trabajadores
(20,30)
(30,50)
(30,70)
(70,90)
(90,100)
Números de empresas
8
17
9
2
4
no me a gutado x que cuando redondeas alugn numero te sale como erronio y ademas aun que hayas acertado la mitad de las preguntas, si has fallado la otra mitad te pone un 0.
Una disculpa por las fallas, cuando te pase centrate en tus resultados que te dan y compara con las soluciones del artículo.
me gusto este tema nunca 100% por que siempre ay error
7. Se tiene los siguientes datos: Xi: 3, 4, 2, 6,3, 4, 5, 3, 4, 5, 5, 4, 6, 2, 3, 4, 5, 6, 4, 5:
Calcule:
a. Media Aritmética, considerando que los datos responden a una variable discreta
b. Media Aritmética considerando que los datos responden a una variable continua (organizados en intervalos de clase)
c. Entable la diferencia entre el inciso a y b, Comente
Hola, una disculpa por los errores, podrías hacernos el favor de señalar para rectificar.
Dispersión se escribe con s y lleva acento.
Múltiples errores en cálculo
Una disculpa por los errores, estamos trabajando por dar el mejor servicio y con sus observaciones vamos lográndolo, en cuanto a la palabra dispersión ya se corrigió, por favor indicanos los otros errores a corregir.