Temas
¿Necesitas un profesor matematicas?
La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones.

Conceptos de Estadística
Población
Una población es el conjunto de todos los elementos a los que se somete a un estudio estadístico.
Individuo
Un individuo o unidad estadística es cada uno de los elementos que componen la población.
Muestra
Una muestra es un conjunto representativo de la población de referencia, el número de individuos de una muestra es menor que el de la población.
Muestreo
El muestreo es la reunión de datos que se desea estudiar, obtenidos de una proporción reducida y representativa de la población.
Valor
Un valor es cada uno de los distintos resultados que se pueden obtener en un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos dos valores: cara y cruz.
Dato
Un dato es cada uno de los valores que se ha obtenido al realizar un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos 5 datos: cara, cara, cruz, cara, cruz.
Variables estadísticas
Las variables estadísticas son de dos tipos: cualitativas o cuantitativas
Variable cualitativa
Las variables cualitativas se refieren a características o cualidades que no pueden ser medidas con números. Podemos distinguir dos tipos:
Variable cualitativa nominal
Una variable cualitativa nominal presenta modalidades no numéricas que no admiten un criterio de orden.
Variable cualitativa ordinal o variable cuasicuantitativa
Una variable cualitativa ordinal presenta modalidades no númericas en las que existe un orden.
Variable cuantitativa
Una variable cuantitativa es la que se expresa mediante un número, por tanto se pueden realizar operaciones aritméticas con ella. Podemos distinguir dos tipos:
Variable discreta
Una variable discreta es aquella que solo puede tomar un número finito de valores entre dos valores cualesquiera de una caraterística.
Variable continua
Una variable continua es aquella que puede tomar un número infinito de valores entre dos valores cualesquiera de una caraterística.
Distribución de frecuencias
La distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente.
Diagrama de barras
Un diagrama de barras se utiliza para de presentar datos cualitativos o datos cuantitativos de tipo discreto.
Los datos se representan mediante barras de una altura proporcional a la frecuencia.
Polígonos de frecuencias
Un polígono de frecuencias se forma uniendo los extremos de las barras mediante segmentos.
También se puede realizar trazando los puntos que representan las frecuencias y uniéndolos mediante segmentos.
Diagrama de sectores
Un diagrama de sectores se puede utilizar para todo tipo de variables, pero se usa frecuentemente para las variables cualitativas.
Los datos se representan en un círculo, de modo que el ángulo de cada sector es proporcional a la frecuencia absoluta correspondiente.
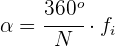
Histograma
Un histograma es una representación gráfica de una variable en forma de barras.
Se utilizan para variables continuas o para variables discretas, con un gran número de datos, y que se han agrupado en clases.
En el eje abscisas se construyen unos rectángulos que tienen por base la amplitud del intervalo, y por altura, la frecuencia absoluta de cada intervalo.
Medidas de centralización
Moda
La moda es el valor que tiene mayor frecuencia absoluta. Se representa por 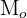 y se puede hallar para variables cualitativas y cuantitativas.
y se puede hallar para variables cualitativas y cuantitativas.
Cálculo de la moda para datos agrupados
1 Todos los intervalos tienen la misma amplitud.
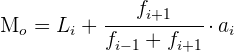
2 Los intervalos tienen amplitudes distintas.
En primer lugar tenemos que hallar las alturas.
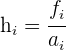
La clase modal es la que tiene mayor altura.
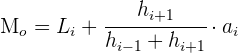
Mediana
Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor. La mediana se representa por 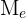 y se puede hallar sólo para variables cuantitativas.
y se puede hallar sólo para variables cuantitativas.
Cálculo de la mediana
1 Ordenamos los datos de menor a mayor.
2 Si la serie tiene un número impar de medidas la mediana es la puntuación central de la misma.
3 Si la serie tiene un número par de puntuaciones la mediana es la media entre las dos puntuaciones centrales.
Cálculo de la mediana para datos agrupados
La mediana se encuentra en el intervalo donde la frecuencia acumulada llega hasta la mitad de la suma de las frecuencias absolutas, es decir, tenemos que buscar el intervalo en el que se encuentre 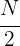 .
.
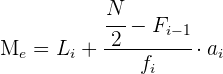
Media aritmética
La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos y se representa por 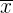
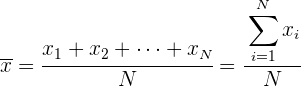
Media aritmética para datos agrupados
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la media es:

Medidas de posición
Cuartiles
Los cuartiles son los tres valores de la variable dividen a un conjunto de datos ordenados en cuatro partes iguales.  y
y  determinan los valores correspondientes al
determinan los valores correspondientes al 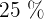 , al
, al 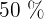 y al
y al  de los datos.
de los datos.

Deciles
Los deciles son los nueve valores que dividen la serie de datos en diez partes iguales. Los deciles dan los valores correspondientes al  , al
, al  y al
y al  de los datos.
de los datos.
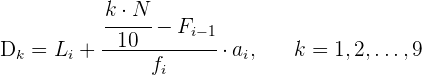
Percentiles
Los percentiles son los 99 valores que dividen la serie de datos en 100 partes iguales. Los percentiles dan los valores correspondientes al  , al
, al 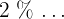 y al
y al  de los datos.
de los datos.
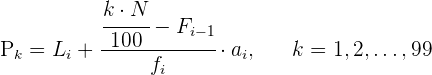
Medidas de dispersión
Las medidas de dispersión nos informan sobre cuánto se alejan del centro los valores de la distribución. Las medidas de dispersión son:
Rango o recorrido
El rango es la diferencia entre el mayor y el menor de los datos de una distribución estadística.
Desviación media
La desviación respecto a la media es la diferencia entre cada valor de la variable estadística y la media aritmética.
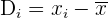
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
La desviación media se representa por 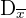
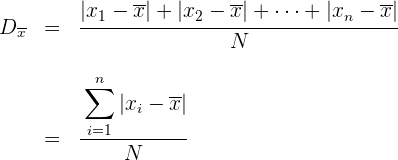
Ejemplo: Calcular la desviación media de la distribución:

Primero calculamos la media

Calculamos la distribución media
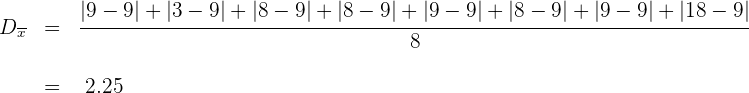
Desviación media para datos agrupados
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la desviación media es:
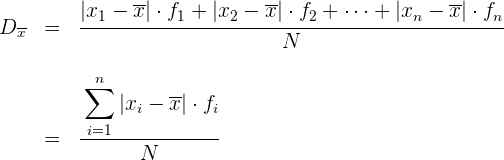
Ejemplo: Calcular la desviación media de la distribución:
 |  |  |  | 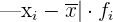 | |
 | 12.5 | 3 | 37.5 | 9.286 | 27.858 |
|---|---|---|---|---|---|
 | 17.5 | 5 | 87.5 | 4.286 | 21.43 |
 | 22.5 | 7 | 157.5 | 0.714 | 4.998 |
 | 27.5 | 4 | 110 | 5.714 | 22.856 |
 | 32.5 | 2 | 65 | 10.174 | 21.428 |
| 21 | 457.5 | 98.57 |
Realizamos las operaciones correspondientes para obtener la tabla.
Realizamos la suma de las últimas cuatro columnas y calculamos la media
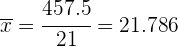
La desviación media es
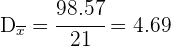
Varianza
La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.
La varianza se representa por 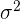 .
.
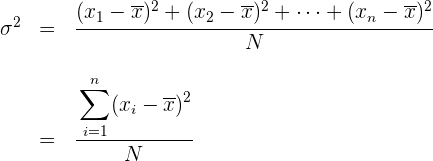
Varianza para datos agrupados

Para simplificar el cálculo de la varianza vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.
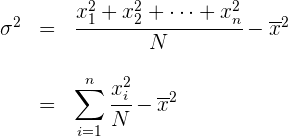
Ejemplo: Calcular la varianza de la distribución:

Primero calculamos la media

Con el valor de la media, ya podemos encontrarla varianza

Ejemplo: Calcular la varianza de la distribución de la tabla:
 |  |  |  | |
|---|---|---|---|---|
 | 15 | 1 | 15 | 225 |
 | 25 | 8 | 200 | 5000 |
 | 35 | 10 | 350 | 12 250 |
 | 45 | 9 | 405 | 18 225 |
 | 55 | 8 | 440 | 24 200 |
 | 65 | 4 | 260 | 16 900 |
 | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |
Realizamos las operaciones correspondientes para obtener la tabla.
Realizamos la suma de las últimas tres columnas y calculamos la media
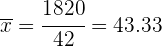
La varianza es
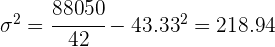
Desviación típica
La desviación típica es la raíz cuadrada de la varianza.
La desviación típica se representa por  .
.
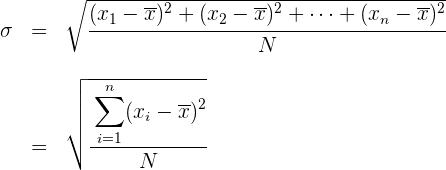
Desviación típica para datos agrupados
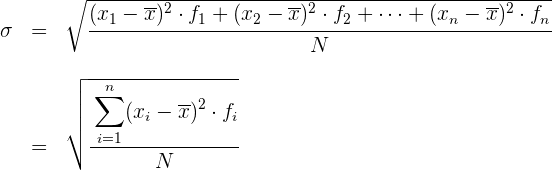
Para simplificar el cálculo vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.

Desviación típica para datos agrupados

Coeficiente de variación
El coeficiente de variación es la relación entre la desviación típica de una muestra y su media.
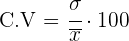
Puntuaciones típicas
Las puntuaciones típicas son el resultado de dividir las puntuaciones diferenciales entre la desviación típica. Este proceso se llama tipificación.
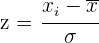
¿Buscas un profesor matematicas Madrid?













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Media de 30. 35. 30. 40. 35. 30. 35.
suma los datos y nos da 235 a eso le dividimos el numero de datos que es 7 se divide 235 entre 7 =33.5 esa es la media o el promedio
Que tanto% de las inversiones establecidas por el empresario entran comprendidas a más de 3.5 desviaciones estándar y a menos de 3.5 desviaciones estándar respecto a la media según el teorema de Chevichev
Segun chevichev seria un 35% al dividirlo entre cien y calculandolo en porcenteaje con la regla de Evalis
Me pueden ayudar por favor.
Necesito determinar la desviación media del siguiente grupo de números en relación al total de las observaciones: 10, 8, 7, 9, 6.
Gracias.):
Al calcular la media y la desviación estándar de 50 datos, ambos resultaron ser iguales a 12. Un chequeo de los datos mostró que en lugar de un dato con valor de 12,8 se había introducido 17,8; corrija la media y la desviación estándar.
Desviación y varianza y tipica12..6..7.3.15.10.18.5