Capítulos
La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.
La varianza se representa por 
.
La fórmula de la varianza
Ejemplos de cálculo de la varianza
1 Calcular la varianza de la distribución: 
Calculamos la media aritmética
Calculamos la varianza
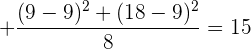
2 Calcular la varianza de la distribución: 
Calculamos la media aritmética
Calculamos la varianza
3 Calcular la varianza de la distribución: 
Usando las mismas etapas como en los ejemplos anteriores, primero calculamos la media aritmética y luego la varianza.
4 Calcular la varianza de la distribución: 
Usando las mismas etapas como en los ejemplos anteriores, primero calculamos la media aritmética y luego la varianza.
5 Calcular la varianza de la distribución: 
Usando las mismas etapas como en los ejemplos anteriores, primero calculamos la media aritmética y luego la varianza.
Varianza para datos agrupados
Para simplificar el cálculo de la varianza vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.
Ejemplo de cálculo de datos agrupados
Calcular la varianza de la distribución de la tabla:
 |  |  |  | |
|---|---|---|---|---|
 |  |  | |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  | |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |
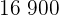Hemos añadido la columna porque queremos hallar su sumatoria 
, que
después dividiremos por 
para obtener la media
Hemos añadido la columna porque queremos hallar su sumatoria 
, que después dividiremos por y al resultado le restaremos la media aritmética al cuadrado 
.
Propiedades de la varianza
1 La varianza será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.
2 Si a todos los valores de la variable se les suma un número la varianza no varía.
3 Si todos los valores de la variable se multiplican por un número la varianza queda multiplicada por el cuadrado de dicho número.
4 Si tenemos varias distribuciones con la misma media y conocemos sus respectivas varianzas se puede calcular la varianza total.
Si todas las muestras tienen el mismo tamaño:
Si las muestras tienen distinto tamaño:
Observaciones sobre la varianza
1 La varianza, al igual que la media, es un índice muy sensible a las puntuaciones extremas.
2 En los casos que no se pueda hallar la media tampoco será posible hallar la varianza.
3 La varianza no viene expresada en las mismas unidades que los datos, ya que las desviaciones están elevadas al cuadrado.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Calcule el segundo cuartil para la tabla de datos dada
IDC f
100 – 134 3
135 – 169 12
170 – 204 19
205 – 239 34
240 – 274 36
275 – 309 19
310 – 344 6
Buenos días, debes revisar la respuesta de ,la pregunta 9, pues es cualitativa ordinal, ya que es el primer apellido y para definirlo, se debe tener el orden alfabético.
Hola agradecemos tus observaciones, pero no encontré el ejercicio que mencionas con su error podrías ser mas especifico, seria de mucha ayuda.
A partir de la siguiente de la siguiente tabla de frecuencia realiza su gráfica número de producto 1 2 3 4 5 frecuencia 35724
Números de trabajadores
(20,30)
(30,50)
(30,70)
(70,90)
(90,100)
Números de empresas
8
17
9
2
4
no me a gutado x que cuando redondeas alugn numero te sale como erronio y ademas aun que hayas acertado la mitad de las preguntas, si has fallado la otra mitad te pone un 0.
Una disculpa por las fallas, cuando te pase centrate en tus resultados que te dan y compara con las soluciones del artículo.