Definición de media aritmética

La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.

es el símbolo de la media aritmética.

Ejemplo

Los pesos de seis amigos son: 84, 91, 72, 68, 87 y 78 kg. Hallar el peso medio.

Media aritmética para datos agrupados

Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la media es:

Ejercicio de media aritmética

En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la puntuación media.

	xi	fi	xi · fi
[10, 20)	15	1	15
[20, 30)	25	8	200
[30,40)	35	10	350
[40, 50)	45	9	405
[50, 60	55	8	440
[60,70)	65	4	260
[70, 80)	75	2	150
		42	1 820

Propiedades de la media aritmética

1 La suma de las desviaciones de todas las puntuaciones de una distribución respecto a la media de la misma igual a cero.

Las suma de las desviaciones de los números 8, 3, 5, 12, 10 de su media aritmética 7.6 es igual a 0:

8 − 7.6 + 3 − 7.6 + 5 − 7.6 + 12 − 7.6 + 10 − 7.6 =

= 0. 4 − 4.6 − 2.6 + 4. 4 + 2. 4 = 0

2 La media aritmética de los cuadrados de las desviaciones de los valores de la variable con respecto a un número cualquiera se hace mínima cuando dicho número coincide con la media aritmética.

3 Si a todos los valores de la variable se les suma un mismo número, la media aritmética queda aumentada en dicho número.

4 Si todos los valores de la variable se multiplican por un mismo número la media aritmética queda multiplicada por dicho número.

Observaciones sobre la media aritmética

1 La media se puede hallar sólo para variables cuantitativas.

2 La media es independiente de las amplitudes de los intervalos.

3 La media es muy sensible a las puntuaciones extremas. Si tenemos una distribución con los siguientes pesos:

65 kg, 69kg , 65 kg, 72 kg, 66 kg, 75 kg, 70 kg, 110 kg.

La media es igual a 74 kg, que es una medida de centralización poco representativa de la distribución.

4 La media no se puede calcular si hay un intervalo con una amplitud indeterminada.

	xi	fi
[60, 63)	61.5	5
[63, 66)	64.5	18
[66, 69)	67.5	42
[69, 72)	70.5	27
[72, ∞ )		8
		100

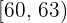En este caso no es posible hallar la media porque no podemos calcular la marca de clase de último intervalo.