Resuelve los siguientes sistemas de ecuaciones por el método de sustitución. En caso de que alguna solución sea una fracción escríbela de la forma .

1

x = ;y =

Despejamos de la segunda ecuación

Sustituímos el valor de en la primera ecuación:

Sustituímos el valor de en la segunda ecuación para calcular :

2

x = ;y =

Quitamos paréntesis:

Despejampos de la segunda ecuación:

Sustituímos el valor de en la primera ecuación y despejamos :

3

x = ;y =

Despejamos de la segunda ecuación

Sustituímos el valor de en la primera ecuación:

Sustituímos el valor de en la segunda ecuación para calcular :

4

x = ;y =

Despejamos de la segunda ecuación

Sustituímos el valor de en la primera ecuación:

Sustituímos el valor de en la segunda ecuación para calcular :

5

x = ;y =

Despejamos de la segunda ecuación

Sustituímos el valor de en la primera ecuación:

Sustituímos el valor de en la segunda ecuación para calcular :

6

x = ;y = ;z =

Despejamos de la tercera ecuación

Sustituímos el valor de en la segunda ecuación:

Multiplicamos la primera ecuación por , sustituimos el valor y despejamos el valor :

Remplazamos el valor de y en la primera ecuación multiplicada por y obtenemos el valor de :

Sustituimos el valor de en y para obtener los valores de y :

Resuelve los siguientes problemas:

7Tenemos € en monedas de y céntimos. ¿Cuántas monedas de cada clase tenemos?

Monedas de céntimos Monedas de céntimos 

En primer lugar pasamos los euros a céntimos:

€ céntimos.

Elegimos las incógnitas:

    • : número de monedas de céntimos.
  • : número de monedas de céntimos.

Obtenemos las ecuaciones relacionando los datos.

    • Tenemos monedas, entonces
  • El valor total es céntimos, entonces

Antes de resolver el sistema obtenemos otro equivalente a él con el que será más fácil operar:

Resolvemos el sistema:

Despejemos de la primer ecuación:

Sustituyamos en la segunda ecuación y resolvamos para

Calculamos el valor de a partir del valor de al sustituir en la primer ecuación:

Tenemos monedas de 50 céntimos y monedas de 10 céntimos.

Si no te has acordado de pasar a un sistema equivalente más sencillo recuerda que tus soluciones serán las mismas, sólo que los cálculos pueden ser un poco más complicados. Lo hacemos por una vez:

Resolvemos el sistema

Despejemos de la primer ecuación:

Sustituyamos en la segunda ecuación y resolvamos para

Calculamos el valor de a partir del valor de al sustituir en la primer ecuación:

Tenemos monedas de 50 céntimos y monedas de 10 céntimos.

8Jaime va a hacer una fiesta en su casa. Va al supermercado y compra paquetes de patatas fritas y botellas de refresco de limón por €. Más tarde vuelve a comprar paquetes de patatas y botella por €. ¿Cuál es el precio de ambos productos?

Patatas fritas  €Botella de refresco  €

Definimos las incógnitas:

    • : precio cada bolsa de patatas fritas.
  • : precio de cada botella de refresco de limón.

Obtenemos las ecuaciones relacionando los datos.

    • En la primera compra obtenemos bolsas de patatas y botellas por €, por lo tanto tenemos .
  • En la segunda obtenemos de patatas y botella por €, por lo tanto obtenemos

Resolvemos el sistema

Despejemos de la segunda ecuación:

Sustituyamos en la primera ecuación y resolvamos para

Calculamos el valor de a partir del valor de al sustituir en la segunda ecuación:

El precio de cada bolsa de patatas es de € y el de cada botella de refresco es de €.

9Dos números suman y el doble de uno de ellos es . ¿Qué números son de menor a mayor?

Primer número  Segundo número 

Definimos las incógnitas:

    • : primer número.
  • : segundo número.

Obtenemos las ecuaciones relacionando los datos.

    • La suma de los dos números es , por lo tanto tenemos .
  • El doble de uno de ellos es , por lo tanto obtenemos

Resolvemos el sistema

Despejemos de la segunda ecuación:

Sustituyamos en la primera ecuación y resolvamos para

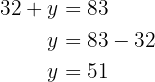
Por lo tanto los números son y .

10Hallar la medida de los lados de un rectángulo cuyo perímetro es 48 y cuyo lado mayor mide el triple que su lado menor.

Lado mayor  Lado menor 

Definimos las incógnitas:

    • : lado mayor.
  • : lado menor.

Obtenemos las ecuaciones relacionando los datos.

    • El perímetro mide , por lo tanto tenemos .
  • El lado mayor mide tres veces el menor, por lo tanto obtenemos

Resolvemos el sistema

Remplazamos la segunda ecuación en la primera:

Calculamos el valor de a partir del valor de al sustituir en la segunda ecuación:

El lado mayor es y el lado menor es .

11En un examen, las preguntas correctas suman un punto y las incorrectas restan medio punto. En total hay preguntas y hay que contestar todas las preguntas. Un alumno obtuvo sobre . Calcular el número de preguntas que contestó de manera correcta e incorrectamente.

Respuestas correctas  Respuestas incorrectas 

Definimos las incógnitas:

    • : respuestas correctas.
  • : respuestas incorrectas.

Obtenemos las ecuaciones relacionando los datos.

    • La suma total de respuestas correctas e incorrectas es , por lo tanto tenemos .
  • La nota final es sobre pero tenemos preguntas así que debemos ajustar el valor obtenido en la prueba multiplicando por 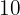. Dado que las respuestas correctas aportan punto y las incorrectas punto, obtenemos

Resolvemos el sistema

Despejemos de la segunda ecuación:

Sustituyamos en la primera ecuación y resolvamos para

Calculamos el valor de a partir del valor de al sustituir en la segunda ecuación:

El número de respuestas correctas fue y el número de respuestas incorrectas fue .

Si tienes dudas puedes consultar la teoría




¿Te ha gustado este artículo? ¡Califícalo!

¿Ninguna información? ¿En serio?Ok, intentaremos hacerlo mejor la próxima vezAprobado por los pelos. ¿Puedes hacerlo mejor?Gracias. Haznos cualquier pregunta en los comentar¡Un placer poder ayudarte! :) 4,00 (25 nota(s))
Cargando...

Marta

➗ Licenciada en Químicas da clase de Matemáticas, Física y Química -> Comparto aquí mi pasión por las matemáticas ➗