Escoge la opción correcta:
1La solución de la inecuación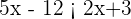 
es...
1Agrupamos los términos en 
a un lado de la desigualdad y los términos independientes en el otro
2Efectuamos las operaciones
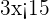
3Despejamos la incógnita
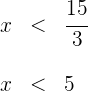
2La solución de la inecuación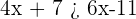 
es...
1Agrupamos los términos en a un lado de la desigualdad y los términos independientes en el otro
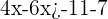
2Efectuamos las operaciones
3Despejamos la incógnita, recordando que al dividir entre un número negativo se invierte elsímbolo
3La solución de la inecuación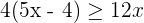 
es...
1Quitamos los paréntesis
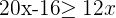
2Agrupamos los términos en a un lado de la desigualdad y los términos independientes en el otro
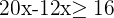
3Efectuamos las operaciones
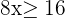
4Despejamos la incógnita
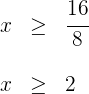
4La solución de la inecuación 
es...
1Quitamos los paréntesis
2Agrupamos los términos en a un lado de la desigualdad y los términos independientes en el otro
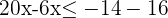
3Efectuamos las operaciones
4Despejamos la incógnita y simplificamos
5La solución como intervalo de la inecuación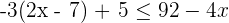 
es...
1Quitamos los paréntesis
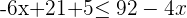
2Agrupamos los términos en a un lado de la desigualdad y los términos independientes en el otro
3Efectuamos las operaciones
4Despejamos la incógnita, recordando que al dividir por un número negativo se invierte la desigualdad
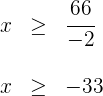
5 Así, la solución en forma de intervalo es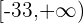 
6La solución como intervalo de la inecuación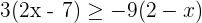 
es...
1Quitamos los paréntesis
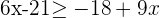
2Agrupamos los términos en a un lado de la desigualdad y los términos independientes en el otro
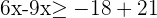
3Efectuamos las operaciones
4Despejamos la incógnita, recordando que al dividir por un número negativo se invierte la desigualdad
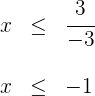
5 Así, la solución en forma de intervalo es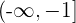 
7La solución de la ecuación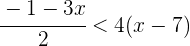 
es...
1Quitamos paréntesis
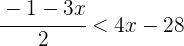
2Quitamos denominadores y operamos
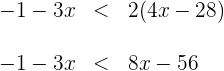
3Agrupamos los términos en a un lado de la desigualdad y los términos independientes en el otro
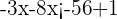
4Efectuamos las operaciones
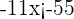
5Despejamos la incógnita
8La solución de la ecuación 
es...
1Quitamos denominadores y operamos
2Agrupamos los términos en a un lado de la desigualdad y los términos independientes en el otro
3Efectuamos las operaciones
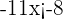
4Despejamos la incógnita
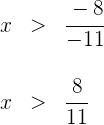
9La solución de la ecuación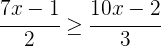 
es...
1Quitamos denominadores y operamos
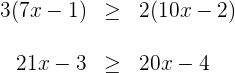
2Agrupamos los términos en a un lado de la desigualdad y los términos independientes en el otro
3Efectuamos las operaciones
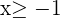
4En intervalos el resultado es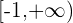 
10La solución como intervalo de la inecuación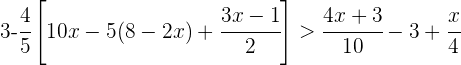 
es...
1Operamos dentro de los corchetes y quitamos paréntesis y corchetes
2Operamos, pasamos a común denominador y quitamos denominadores
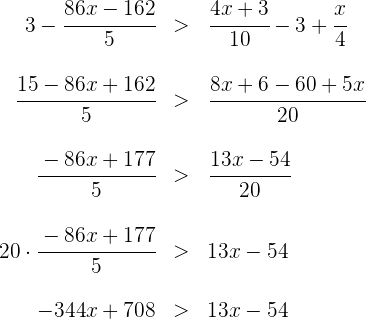
3Agrupamos los términos en a un lado de la desigualdad y los términos independientes en el otro
4Efectuamos las operaciones
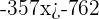
5Despejamos la incógnita y simplificamos
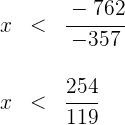
6Por tanto, la solución de esta inecuación en forma de intervalo es 
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el ejercicio 9 de inecuaciones hay un error en el resultado, crec. Pone (-4,3) U (3,4) y creo que deberia ser (-4,-3)U(3,4). S no no lo comprendo.
Hola, fue un error nuestro discúlpanos ya se corrigió y gracias por tu ayuda.
¿Por qué el segundo intervalo del último ejercicio es abierto?
Me podrían por favor Ayudar a resolver esta inecuación cuadrática
(2X-4)(3X-6) > 0
Hola, podrias describir el ejercicio ya que no me señala el artículo correspondiente a tu pregunta.
48x+12>108
10(×+1)+<6(2×+1)
Muy interesante ☺️ por favor me da la solución de X (x-2) 23