Temas

¿Qué es la solución de una inecuación?
La solución de una inecuación es el conjunto de valores de las variables que verifica la inecuacíón. El conjunto de soluciones genera una región geométrica en la recta real si la inecuación es de una variable, o en el plano si es de dos.
Ejemplo:
- La inecuación
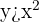 nos genera la siguiente región en el plano.
nos genera la siguiente región en el plano.

Sistema de inecuaciones
La solución de un sistema de inecuaciones es la intersección de las regiones que corresponden a la solución de cada inecuación.
Un sistema de inecuaciones se dice que es lineal, si en ambos lados de cada inecuación aparece una expresión de primer grado.

Ejemplos de sistemas de inecuaciones lineales con dos incógnitas
Vamos a resolver el sistema:
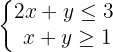
Representamos la región solución de la primera inecuación
1 Transformamos la desigualdad en igualdad.

2 Damos dos valores a una de las dos variables , con lo que obtenemos dos puntos


3 Al representar y unir estos puntos obtenemos una recta

Finalmente tomamos un punto, por ejemplo el (0, 0), lo sustituimos en la desigualdad. Si se cumple, la solución es el semiplano donde se encuentra el punto, si no, la solución será el otro semiplano

 Sí se cumple la inecuación
Sí se cumple la inecuación
Como se cumple, la solución es el semiplano donde se encuentra (0, 0) incluida la recta

Representamos la región solución de la segunda inecuación
1 Transformamos la desigualdad en igualdad.
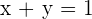
2 Damos dos valores a una de las dos variables, con lo que obtenemos dos puntos
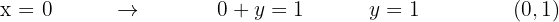
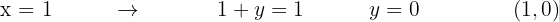

3 Tomamos un punto, por ejemplo el (0, 0) de nuevo, lo sustituimos en la desigualdad.
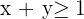
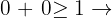 No se cumple la inecuación
No se cumple la inecuación
Como no se cumple, la solución es el semiplano donde no se encuentra (0, 0), incluida la recta

La solución es la intersección de las regiones soluciones.

Ejemplos de sistemas de inecuaciones lineales con una incógnita
Se resuelve cada inecuación por separado. El conjunto solución del sistema es la intersección de los conjuntos soluciones de ambas inecuaciones.
1 
Resolvemos la primera inecuación

Resolvemos la segunda inecuación
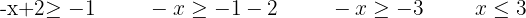
Consideramos la intersección de las soluciones

El intervalo de soluciones es [−1, 3]
2 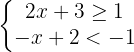
Resolvemos la primera inecuación

Resolvemos la segunda inecuación
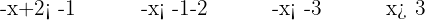
Consideramos la intersección de las soluciones

El intervalo de soluciones es (3, ∞)
3 
Resolvemos la primera inecuación

Resolvemos la segunda inecuación

Consideramos la intersección de las soluciones

No tiene solución.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
INECUACION CUADRATICA RESOLVER x^2 − 4x + 7 > 0
Necesito ayuda con este problema 2x<(2x+1)(x-2)-2x(x-7)
Xfi
Por favor ayúdenme con este ejercicio que hay que resolver por medio de inecuaciones.
En un depósito cada tanque de leche tiene una capacidad de 200 litros. ¿Cuál es la cantidad máxima de tanques que puede cargar un camión cuya capacidad es de 50000 litros de leche?
necesito ayuda con esta inecuacion cuadratica: -2x al cuadrado +18x-36>0
×-18al cuadrado mas o menos√18al cuadrado-4(-2)(-36) dividido entre2×(-2)
×18mas o menos√18+-144. Dividido por-4
×18mas o menos√-126÷-4
×18+63/-4. × 18+63/-4. ×18-63)-4
×81/-4. ×-45/-4
×=-20,25. ×=11,25
Deberías hacer una tabla de valores para poder estudiar el signo y después escoger las soluciones adecuadas
Necesito q me respondan a esta ecuación
X²(x+4)
______>0
(X+1)(x+2)