1 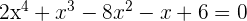
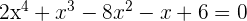
1 Tomamos los divisores del término independiente: 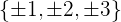 .
.
2 Aplicando el teorema del resto sabremos para que valores la división es exacta.
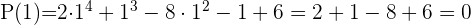
3 Dividimos por Ruffini (División sintética).
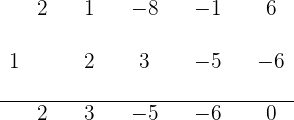
4 Por ser la división exacta, 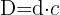 .
.

Una raíz es 
5 Continuamos realizando las mismas operaciones al segundo factor.
6 Volvemos a probar por  porque el primer factor podría estar elevado al cuadrado.
porque el primer factor podría estar elevado al cuadrado.
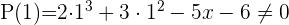
7 Probamos con  .
.


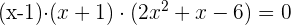
Otra raíz es 
8 Como el tercer polinomio ya es de segundo grado, podemos factorizarlo:
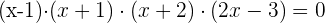
Las soluciones son: 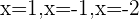 y
y 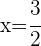
2 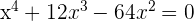
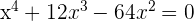
1 Sacamos factor común 
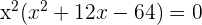
2 Como tenemos un producto igualado a cero o un factor es cero o el otro factor es cero o los dos son cero
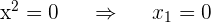
3 Factorizamos el segundo polinomio, que es de segundo grado
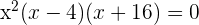
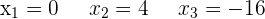
3 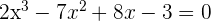
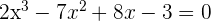
1 Tomamos los divisores del término independiente: 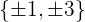 .
.
2 Aplicando el teorema del resto sabremos para que valores la división es exacta.
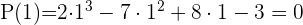
3 Dividimos por Ruffini
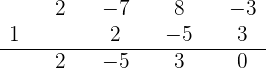
4 Por ser la división exacta, 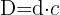
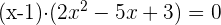
5 Continuamos realizando las mismas operaciones al segundo factor.
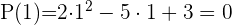

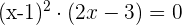
Las raíces son:  y
y 
4 

1 Tomamos los divisores del término independiente: 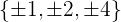
2 Aplicando el teorema del resto sabremos para que valores la división es exacta
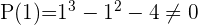
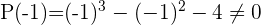
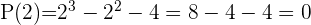
3 Dividimos por Ruffini.

4 Por ser la división exacta, 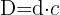
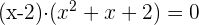
5 Descomponemos el segundo factor resolviendo la ecuación de segundo grado
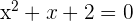
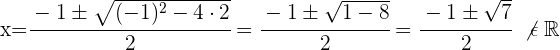
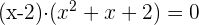
Como la ecuación no tiene solución solo hay una raíz:  .
.
5 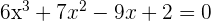
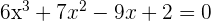
1 Tomamos los divisores del término independiente: 
2 Aplicando el teorema del resto sabremos para que valores la división es exacta
P(1) = 6 · 1³ + 7 · 1² − 9 · 1 + 2 ≠ 0
P(−1) = 6 · (−1)³ + 7 · (−1)² − 9 · (−1) + 2 ≠ 0
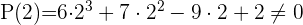
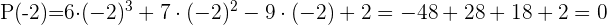
3 Dividimos por Ruffini
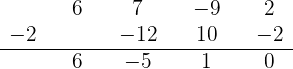
4 Por ser la división exacta, 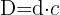
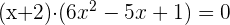
5 Descomponemos el segundo factor resolviendo la ecuación de segundo grado


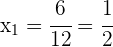

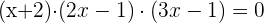
Raíces:  ,
,  y
y 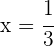
6 

1 Tomamos los divisores del término independiente: {±1, ±2, ±3, ±4, ±6, ±12}
2 Aplicando el teorema del resto sabremos para que valores la división es exacta
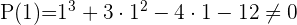
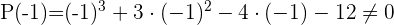
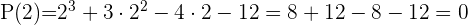
3 Dividimos por Ruffini.
4 Por ser la división exacta, 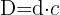 .
.

5 Descomponemos el segundo factor resolviendo la ecuación de segundo grado
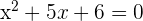
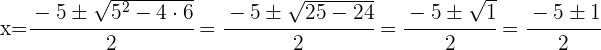

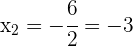

Las soluciones son: 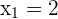 ,
, 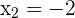 y
y  .
.



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
x²-6x+8=0
x²+6x=0-8
4x=-8
x=-8/4
x=-2
Hola Valeria, lamento la intromisión, si aún necesitas la respuesta, la ecuación es de segundo grado porque la letra x² es la de mayor exponente, debido a que no tienes término semejantes, como x+x, o x²+x² (por ejemplo) no puedes operarios de manera directa. Puedes utilizar la fórmula de segundo general de segundo grado (Que la puedes encontrar en esta página web y te explica cómo usarla, es muy sencillo) o puedes hacer una factorización, tus resultados son x=4 y x=2.
Me parece que el ultimo ejercicio (la tricuadrada) se puede hacer de otra forma ya que hace x^3=t cuando en realidad si se hace x^6=t^3 y x^3=t te da t^3-7t+6 lo cual haciendo un sencillo ruffini te da las x como resultado t=-3 t=2 y t=1 y al volver a pasarlo a las x te da como resultado x1= ∄ y x2= ∄ (al ser la raiz cuadrada de -3) , x3=raiz cuadrada +2, x4= raiz cuadrada -2, x5=+1 y x6=-1. Saludos.
Si haces x^6=t^3 te da x^2=t o x^3=t^(3/2) lo cual complica en vez de facilitar la ecuación, además de que la expresión x^3=t esta mal.
resolver la ecuacion x−4
3
− 5 = 0
X=4 yx= 2
2X=4+2
X=6/2
X=3